Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Волгоградский государственный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

14

.doc

Скачиваний:

35

Добавлен:

25.03.2016

Размер:

1.9 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 86 7 8 > Следующая >>>

21.1Дебаевское экранирование Рассмотрим потенциал неподвижного точечного заряда в изотропной плазме и запишем Фурье-образы уравнений , (1.43) и E(r) = – grad(r). (4.4) : ikD(k, ) = 4_e(k, ), (6.7) E(k, ) = –ik(k, ). (6.8) Уравнение (6.7) с учетом соотношения (3.32) можно преобразовать к виду , который совместно с уравнением (6.8) дает . (6.9) Если поле создано одним точечным зарядом, находящимся в точке r₀, то _e(r, t) = e(r₀), соответственно . Подставляя это соотношение в уравнение (6.9), получим . Проведем обратное преобразование Фурье вида (3.27), вернувшись к переменным r и t:	21.2равной плотности вероятности обнаружить в момент времени t частицу с импульсом p в окрестности точки r. Функция распределения замкнутой системы удовлетворяет уравнению Лиувилля df/dt = 0. Если электроны испытывают рассеяние, например, при столкновениях с ионами или нейтральными атомами, уравнение Лиувилля принимает вид кинетического уравнения Больцмана (6.11) Здесь  = 1/ – время релаксации системы, – частота столкновений, f₀ – равновесная, невозмущенная электромагнитным полем, функция распределения системы, к которой она релаксирует с постоянной времени  при выключении поля. Обозначим в уравнении (6.11) f = f – f₀ – вызванное электрическим полем малое возмущение функции распределения. Пусть магнитное поле отсутствует. Тогда производная импульса электрона, то есть сила, действующая на него, определяется только электрическим полем 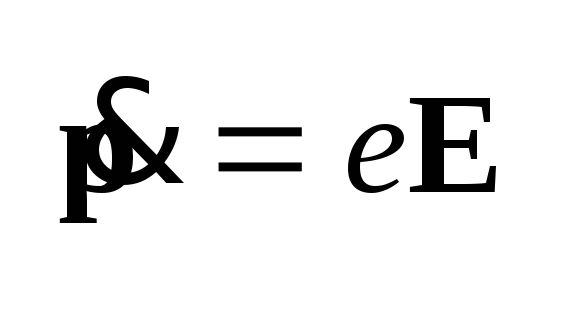. В рамках линейной электродинамики в уравнении (6.11) следует оставить только линейные по полю слагаемые, а слагаемые, содержащие произведение Еf, квадратичные по полю, должны быть отброшены. Тогда Фурье-образ уравнения (6.11) принимает вид . Решение этого уравнения есть . (6.12)	21.3 что . (6.16) В случае бесстолкновительной плазмы, то есть для  = 0, что соответствует бесконечной проводимости по постоянному току, неопределенность, возникающую в формуле (6.16) при  = 0, раскроем по правилу Лопиталя: . Таким образом, , (6.17) где обозначено – (6.18)
22. 1Обобщенная проницаемость плазмы Формулу (6.16) для продольной диэлектрической проницаемости изотропной плазмы удобно записывать в инвариантном виде . (6.20) Поперечная проницаемость плазмы, как следует из формулы (3.32) является коэффициентом пропорциональности между электрическим полем E_, перпендикулярным волновому вектору k, и обобщенной индукцией D. Запишем в инвариантном виде связь (3.29) обобщенной индукции с электрическим полем, учитывая формулу (6.15): . Преобразование подынтегрального выражения в этом соотношении можно обосновать, записав интегралы в координатной форме и направив ось х вдоль вектора Е, а ось у вдоль вектора k. Сравнивая правую часть формулы с левой, непосредственно получаем	22.2 – (6.25) плазменная (ленгмюровская) частота электронов. Проводя аналогичное интегрирование в формуле (6.18), получим: . (6.26) В металлах дебаевский радиус экранирования порядка 10^–7 см, в полупроводниках порядка 10^–5 см, в термоядерной плазме 10^–3 ... 10^–4 см, в ионосфере 10^–1 см, а в межпланетной плазме 10³ см. В предельном случае длинноволновых колебаний знаменатель подынтегрального выражения в формулах (6.23) и (6.24) можно разложить по степеням малого параметра . Для бесстолкновительной плазмы при   0 получим . (6.27) Мнимая часть обобщенной продольной проницаемости плазмы (6.27) растет с ростом волнового вектора. Так как в изотропной среде именно мнимая часть обобщенной проницаемости обусловливает диссипацию энергии поля, можно сделать вывод, что с уменьшением длины волны будет увеличиваться затухание продольных колебаний поля.
23.1Магнитогидродинамика плазмы Помимо кинетического рассмотрения, использованного в предыдущих двух разделах, часто используется другой, более грубый, гидродинамический метод описания. В сложных задачах гидродинамический метод часто используется для оценочного рассмотрения и основан на том, что в уравнения Максвелла функция распределения непосредственно не входит. В эти уравнения входят плотность индуцированного заряда и плотность индуцированного тока, которые выражаются через интеграл вида от функции распределения , (6.13) . Иначе говоря, в уравнения Максвелла входят только среднее значение скорости частиц среды. В уравнения же механики, определяющие характер реакции среды на поле, скорость входит непосредственно. Если детали фактического распределения частиц по скоростям мало сказываются на характере реакции среды на внешнее поле, возможно гидродинамическое описание движения среды, в которое с самого начала входит только средняя скорость. В гидродинамическом приближении свойства среды описываются пятью скалярными величинами: тремя компонентами средней скорости частиц среды и двумя термодинамическими величинами, описывающими внутреннее состояние среды в каждой точке.	23.2. Продольная и поперечная компоненты плотности тока при этом имеют вид 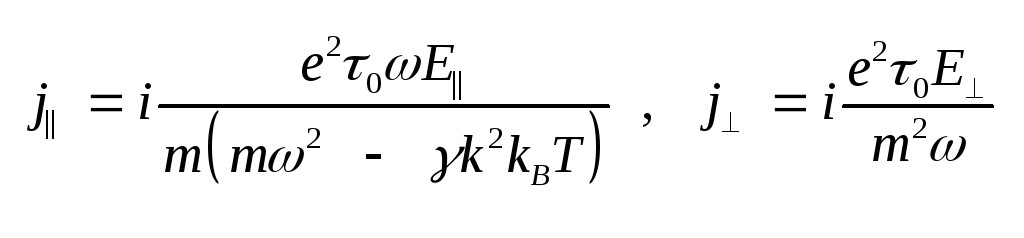. (6.32) Формулы (6.28) – (6.32) написаны для одной из компонент плазмы. Поскольку ток обусловлен всеми ее компонентами, в формулах (6.32) следует подразумевать суммирование по всем компонентам. Из соотношений (6.32) непосредственно получаются выражения для продольной и поперечной проводимостей плазмы , (6.33) где производится суммирование по всем компонентам плазмы. В соответствии с формулами – (3.16) и (6.25) для продольной и поперечной обобщенных проницаемостей изотропной немагнитной плазмы получаем	23.3 Тогда уравнение движения (6.28) принимает вид уравнения Навье – Стокса [v/t + (v)v] = –p + [jB]/c + F_c. (6.35) Уравнение движения (6.35) помимо уравнения непрерывности (6.29) и уравнений Максвелла crotE = –B/t, crotB = 4j, divB = 0, (6.36) в которых для низкочастотных колебаний опущен ток смещения и положено для немагнитной плазмы В = Н, необходимо дополнить материальным уравнением j = (E + [vB]/c) (6.37) Отметим, что в силу уравнений (2.7) комбинация E + [vB]/c есть электрическое поле в системе, движущейся вместе с плазмой. Именно в такой системе определен закон Ома j_i = _ikE_k, (1.40) . Выразим из уравнения (6.37) электрическое поле E = j/ – [vB]/c и подставим это значение в первое из уравнений Максвелла (6.36), учтя при этом второе и третье уравнения: B/t = rot[vB] + с²В/(4). (6.38) Для неподвижной среды уравнение (6.38) принимает вид уравнения диффузии: с²В – 4B/t = 0. (6.39) Из структуры уравнения (6.39) можно определить время диффузии магнитного поля на характерное расстояние L, на котором существенно изменяется магнитное поле: t_d = 4L²/с². (6.40) Другому предельному случаю отвечает движущаяся среда с очень высокой проводимостью. При    уравнение (6.38) переходит в B/t = rot[vB] = (B)v – (v)B – Bdivv + vdivB Последнее слагаемое в правой части этого уравнения равно нулю в силу третьего уравнения Максвелла (6.36), а третье слагаемое может быть преобразовано с учетом уравнения непрерывности (6.29): .	23.4 В этом случае в правой части уравнения (6.35) отсутствует сила F_с, а в правой части уравнения (6.38) отсутствует второе слагаемое. К этим уравнениям необходимо еще добавить уравнение состояния. При колебательных процессах в жидкости давление р обычно связано с плотностью  соотношением p = s², (6.44) где s – скорость звука в среде. Линеаризуем уравнения (6.35), (6.36) и (6.44) совместно с уравнением непрерывности (6.29) для малых отклонений от положения равновесия  = ₀ + ₁, р = р₀ + р₁, В = В₀ + В₁. Полагая, что v₀ = 0, получим . Эту систему можно разрешить относительно скорости ²v/t² – s²graddivv + [v_arotrot[vv_a]] = 0. (6.45) Здесь – альвеновская скорость. Будем искать решение уравнения (6. 45) в виде плоской магнитогидродинамической волны v = v_aexp(ikr – it). Подстановка в уравнение (6.45) дает . (6.46) Если волна распространяется перпендикулярно магнитному полю, то (kv_a) = 0 и уравнение (6.46) упрощается: . Поскольку направления векторов k и v должны совпадать,
24. 1Поверхностные волны Возьмем ротор от уравнения (1.28) и подставим в него уравнение . (1.44) с учетом материального уравнения (1.42). Для среды без сторонних зарядов и токов получим . Пусть среда является неоднородной, но изотропной и немагнитной ( = 1). Для гармонической волны в такой среде без пространственной дисперсии получаем: . (7.1) Можно также получить уравнение относительно магнитного поля Н = В: . (7.2) Важной особенностью неоднородных сред являются новые решения уравнений (7.1) и (7.2), которые не существуют в пространственно-однородных средах. Наиболее простой вид такие новые моды электромагнитных волн имеют в предельном случае резкой границы раздела двух сред.	24.2 B₁_n = B₂_n. (1.34) D₂_n – D₁_n = 4. (1.35) H_m__S = H_v__S, E_m__S = E_v__S, D_mn_S = D_vn_S. (7.5) Решения уравнений (7.3) и (7.4), описывающие поверхностные волны, должны стремиться к нулю при z  , поэтому будем их искать в виде H_m = H_m₀exp(iqx – k_mz), H_v = H_v₀exp(iqx + k_vz). (7.6) Подставляя соотношения (7.6) в уравнения (7.3) и (7.4), получим: , , 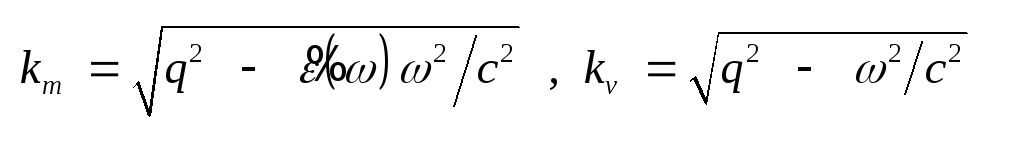. (7.7) Из равенства тангенциальных компонент магнитного поля (7.5) следует, что H_m₀ = H_v₀ = H₀. Равенство тангенциальных компонент электрического поля означает, что 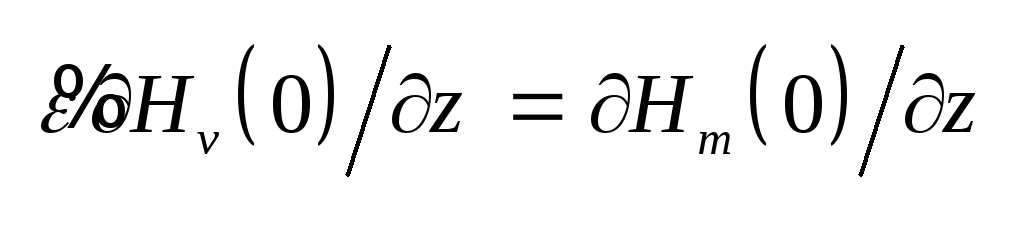. Из этого условия получается , или . (7.8) Уравнение (7.8) имеет решение лишь при . закон дисперсии: . 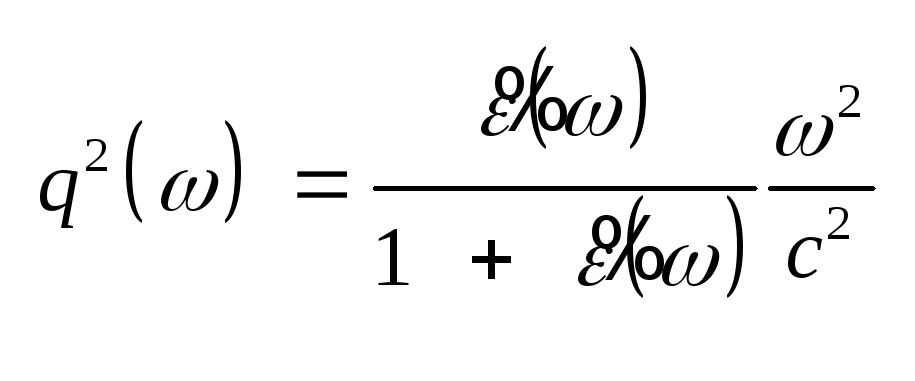(7.9)

			При стремлении R к нулю значение \|A_S\|_R также стремится к нулю. Таким образом, все компоненты векторного потенциала оказываются непрерывной функцией координат и в том случае, когда имеется резкая граница раздела сред. Рассмотрим систему линейных токов, сосредоточенных в ограниченной области, причем все пространство между проводниками заполнено однородным магнетиком с проницаемостью . при такой постановке задачи все линейные токи представляют собой замкнутые витки. Наряду с током I_i, важной характеристикой такого витка является магнитный поток через контур витка . (5.12) Подставляя формулу (5.8) в уравнение (5.12), видим, что потоки и токи связаны между собой линейно , (5.13) где – (5.14) взаимная индуктивность i-го и j-го проводников (при i  j). Величина L_ii называется индуктивностью i-го проводника. Коэффициенты L_ij зависят от геометрии системы: формы, размеров и взаимного расположения проводников. По аналогии с электростатической теоремой взаимности (4.13) и (4.14) можно доказать, что матрица взаимных индуктивностей симметричная: L_ij = L_ji. (5.15). Вводя матрицу (симметричную) , обратную к матрице L_ij, можно переписать формулу (5.13) в виде . (5.16)	Соотношение (5.6), таким образом, позволяет найти векторный потенциал А по заданному распределению сторонних токов. Взяв ротор от выражения (5.6) с учетом соотношения (5.3) и материального уравнения (1.37), получим . (5.7) Из формулы (5.7) видно, что напряженность поля Н в пространственно-неоднородном магнетике при заданном распределении сторонних токов j_e такая же, какой она была бы в отсутствии всякой среды. Будем рассматривать распределение поля только в области вне проводников, достаточно тонких, так что направление тока в данной точке проводника совпадает с направлением dl – элемента длины проводника. Такую систему принято называть системой линейных токов. Тогда, выполняя в соотношениях (5.6) и (5.7) интегрирование по поперечному сечению проводников, получим , (5.8) , (5.9) где I_i – полный ток, протекающий по i-му проводнику. Выражение (5.9) представляет собой закон Био – Савара.
			сти свободной энергии F = W – TS равно . (5.20) Соответственно, изменение плотности потенциала G = F – BH/(4) составляет . (5.21) Кинетические явления в магнитном поле Магнитное поле оказывает влияние на поток электрических зарядов и тепла, возникающих в среде под действием температуры и электрического поля. Как показано в п. 4.6, эти потоки могут быть записаны с учетом соотношения (4.70) в виде уравнений (4.71) и (4.75) E = j + gradT, (5.22) s = j – kgradT, (5.23) где  = 1/,  = –/,  = /. При включении магнитного поля с напряженностью Н кинетические коэффициенты , ,  и k в уравнениях (5.22) и (5.23) начинают зависеть от Н. Если магнитное поле слабое, эти коэффициенты можно разложить в ряд по степеням Н. Ограничиваясь линейными членами, получим E = ₀j + ₀gradT + RHj + NHgradT, (5.24) s = ₀j – k₀gradT + NTHj + LHgradT. (5.25) Нулевой индекс у коэффициентов , ,  и k означает, что их значения берутся в отсутствии магнитного поля. В коэффициентах при HgradT в уравнении (5.24) и Hj в уравнении (5.25) учтен принцип Онсагера вида (4.70). Слагаемое RHj в уравнении (5.24) описывает влияние магнитного поля на ток. В соответствии с этим выражением, магнитное поле приводит к появлению электрическому поля, перпендикулярного току и пропорционального напряженности магнитного поля и току. Это явление называется эффектом Холла.	(5.17) где интегрирование выполняется только по объему проводников. Если магнитное поле создается системой линейных токов, то в соотношении (5.17) можно выполнить интегрирование по поперечному сечению проводников. С учетом соотношения (5.12) получаем . (5.18) Выражение (5.18) можно преобразовать так, чтобы энергия выражалась только через токи I_i или потоки Ф_i. Воспользовавшись соотношениями (5.13) и (5.15), получаем . (5.19) Рассмотрим вопрос о замкнутости системы, магнитная энергия которой определена выражением (5.18). Энергия замкнутой системы должна сохраняться. С другой стороны, проинтегрировав по всему пространству уравнение w/t + divS = –(j + j_e)E, (1.46) и учитывая, что на бесконечности поля, созданные ограниченной системой проводников, затухают, получим, что энергия (5.18) системы сохраняется, если обращается в нуль интеграл . В общем случае этот интеграл определяет работу электромагнитного поля над средой, то есть уменьшение энергии электромагнитного поля. При протекании постоянного тока по обычным проводникам уменьшение энергии поля связано с выделением джоулева тепла и компенсируется за счет источников: электрических батарей, аккумуляторов и т. п
		Поэтому даже в переменных полях уравнения (5.31) и (5.32) принимают вид: , (5.36) . (5.37) Уравнения (5.36) и (5.37) называются, соответственно, первым и вторым уравнениями Лондонов. Обычно в правой части уравнения (5.36) пренебрегают вторым слагаемым, считая плотности тока достаточно малыми. Уравнение (5.37), записанное в виде 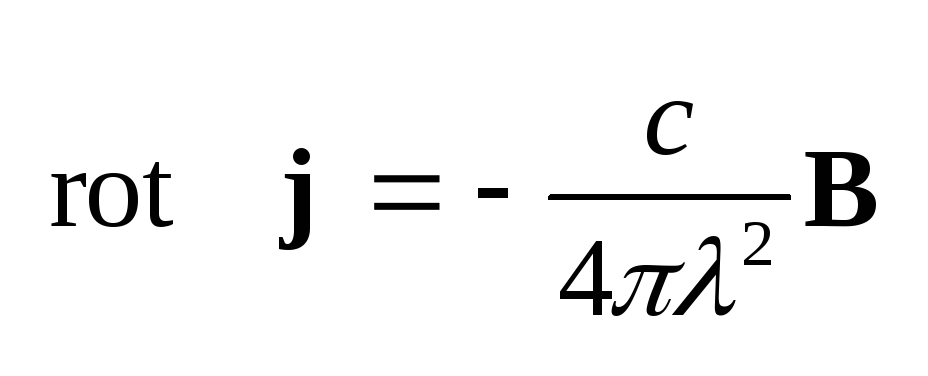, (5.38) является материальным уравнением сверхпроводника. Для сверхпроводящего полупространства x > 0 его можно записать в виде ²d²B/dx² = B. Затухающее на бесконечности в силу эффекта Мейсснера – Оксенфельда решение этого уравнения имеет вид B(x > 0) = B₀exp(–x/), то есть величина , определенная соотношением (5.33), описывает глубину проникновения постоянного магнитного поля в сверхпроводник и называется лондоновской глубиной проникновения	. (1.8) принимает вид . Если следить не за фиксированными электронами, а полем их скоростей в фиксированной точке пространства, то, учитывая, что dv/dt = v/t + (vgrad)v = v/t + grad(v²/2) – [vrotv], уравнению движения электронов можно придать вид уравнения Эйлера: . Учитывая, что j = env, где n – концентрация электронов, перепишем уравнение движения электронной жидкости в сверхпроводнике в виде 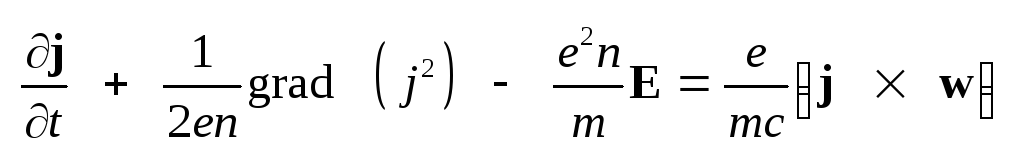, (5.31) где обозначено , (5.32) 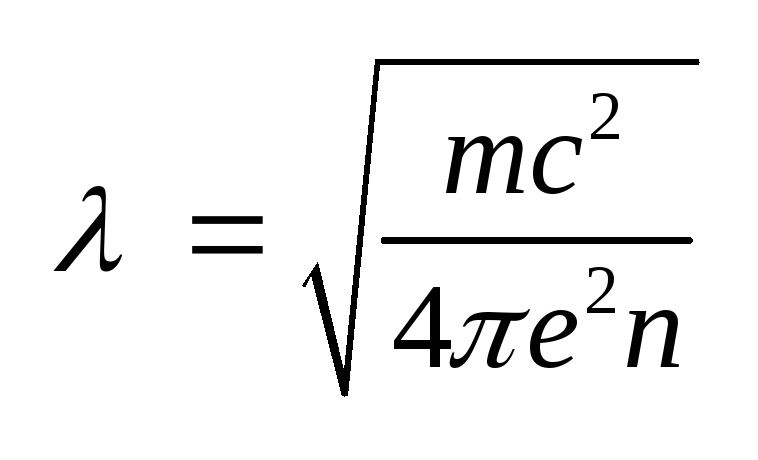. (5.33) В соотношении (5.32) учтено, что сверхпроводник является парамагнитным металлом и можно принять В = Н. Возьмем ротор от обеих частей уравнения (5.31) и с учетом уравнения Максвелла (1.28) получим, что: enw/t = rot[jw]. (5.34) Найдем теперь полную внутреннюю энергию сверхпроводника как сумму энергии магнитного поля и кинетической энергии сверхпроводящих электронов:	Такие оболочки (3d) имеются у элементов подгруппы железа (железо, кобальт, никель). По аналогии с соотношением (4.58), полученным для сегнетоэлектриков, свободную энергию однородного ферромагнетика во внешнем магнитном поле, опуская энергию самого магнитного поля, можно записать в виде: G(M, H, T) = G₀(M², T) – MH, (5.28) где первое слагаемое учитывает свободную энергию ферромагнетика в отсутствии поля, а второе – энергию его взаимодействия с магнитным полем. Величина G₀ в формуле (5.28) зависит от квадрата модуля магнитного момента, так как появление спонтанной намагниченности связано с обменными силами, которые определяются только взаимной ориентацией соседних спинов и не зависят от их ориентации относительно кристаллографических осей. Разлагая функцию G₀(M², T) в ряд по степеням M² и повторяя рассуждения, приведенные в п. 4.5 для сегнетоэлектриков, нетрудно получить формулы (5.27). В постоянном и однородном поле на магнетик действует сила, анализ которой аналогичен проведенному в п. 4.3 и 4.5. Заменяя в формулах . (4.45) и , (4.46)  на ^–1 и Е на В, получаем: 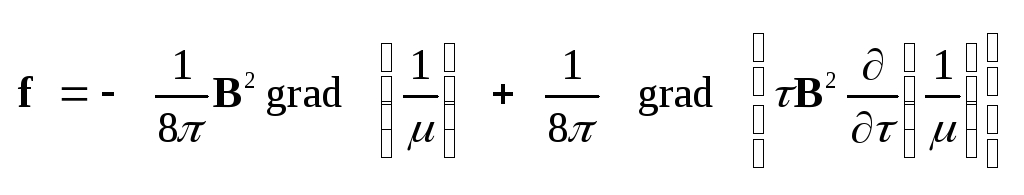. (5.29)
		При таких столкновениях энергия электрона сохраняется, а импульс меняется на противоположный, то есть происходит рассеяние назад. Скорость электрона в переменном высокочастотном поле меняется по закону (6.2), а для его средней за период поля энергии получаем с учетом соотношения (6.3): , где p₀ = mv₀. Пусть в момент t = t₀ происходит мгновенное упругое столкновение с изменением импульса на обратный, то есть p(t₀ + 0) = p(t₀ – 0). Тогда . Средняя за период энергия электрона после столкновения равна , а изменение энергии при столкновении составит . . .	. 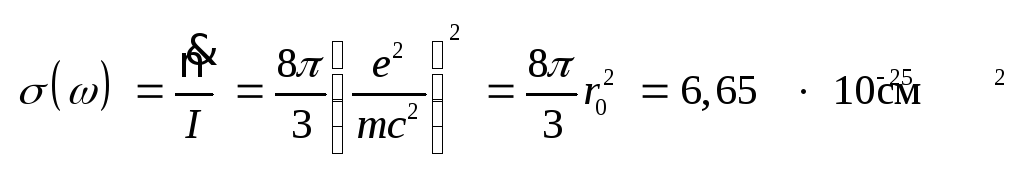(6.4) Здесь учтено, что поток энергии в бегущей волне I = cE²/(8), r₀ – классический радиус электрона. В первом порядке по v/c следует учесть силу Лоренца в уравнении движения по оси z: . (6.5) Это уравнение показывает, что в первом приближении по v/c электрон колеблется вдоль оси z с удвоенной частотой, описывая фигуру Лиссажу – восьмерку в плоскости xz. Эта восьмерка сильно вытянута вдоль оси х, так как отношение амплитуд колебаний по осям z и х порядка v/c. Сечение рассеяния для второй гармоники составляет (2) = ()E_k/(mc²) << (). В следующих приближениях по v/c появляются и следующие гармоники, но вычислять их надо на основе релятивистских уравнений движения, так как они порядка v²/c² и выше. Для круговой поляризации поля все нелинейные эффекты исчезают, так как скорость электрона все время параллельна направлению магнитного поля и сила Лоренца равна нулю. Для свободного электрона, взаимодействующего с электромагнитным полем, классическая теория, включая и формулу Томпсона (6.4), применима при условии ħ << mc², которое выполняется вплоть до гамма-излучения. Для коротковолнового излучения с длиной волны порядка ħ/mc  10^–10 см (комптоновская длина волны) рассеяние происходит с изменением частоты рассеянного света (эффект Комптона).	, (6.2) где v₀ – начальная скорость электрона. Электрон колеблется в поле, и его средняя кинетическая энергия колебательного движения равна . (6.3) Смещение электрона за период поля r, отнесенное к длине волны  = с/, при этом порядка v/c, поэтому в нерелятивистских задачах поле, действующее на электрон, мало отличается от гармонического. Для того чтобы учесть члены первого порядка по v/c, разложим электрическое поле по степеням r и ограничимся линейным слагаемым: . Подставляя это выражение в уравнение (6.1) и учитывая, что в силу уравнения Максвелла (1.28) в гармонической волне rotE = –B/c, получим после усреднения по периоду поля:

<<< < Предыдущая 1 2 3 4 56 / 86 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
28.04.2019300.03 Кб1613 Представление данных в форме описание.doc
#
05.08.201971.17 Кб713-18.doc
#
25.03.2016169.84 Кб4313. Показательные и логарифм. уравнения.docx
#
27.05.20153.27 Mб79138_zapolsky.pdf
#
28.04.2019359.42 Кб6014-16 Представление данных в табличной форме(дл....doc
#
25.03.20161.9 Mб3514.doc
#
10.11.2019496.13 Кб414001-2004BVRUS.doc
#
26.04.201935.08 Кб215,17,20,22, 43,58,63,67 .docx
#
27.05.201514.06 Mб36158.rtf
#
12.11.201914.03 Mб7158.rtf
#
16.12.201851.75 Кб016-20 билеты.docx