|
1.1
Усреднение микроскопических
уравнений Максвелла
Формальный
переход к макроскопическому
описанию электромагнитного
поля можно осуществить
путем усреднения положения
атомов. Для того чтобы после
усреднения тело представляло
собой сплошную среду, размеры
области, по которой
производится усреднение,
должны быть велики по
сравнению с межатомными
расстояниями. С другой
стороны, эти размеры должны
быть малы по сравнению с
расстояниями, на которых
меняется макроскопическое
поле. Так возникает понятие
физически бесконечно
малого объема с размерами,
удовлетворяющими
указанным условиям.
Микроскопические
электрическое e(r,
t)
и магнитное b(r,
t)
поля в среде с зарядами
должны удовлетворять
уравнениям Максвелла,
дополненными уравнением
непрерывности:
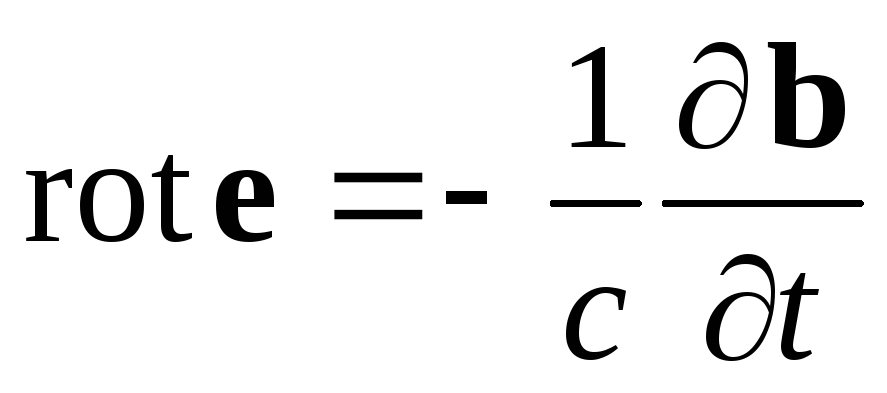 ,
(1.1) ,
(1.1)
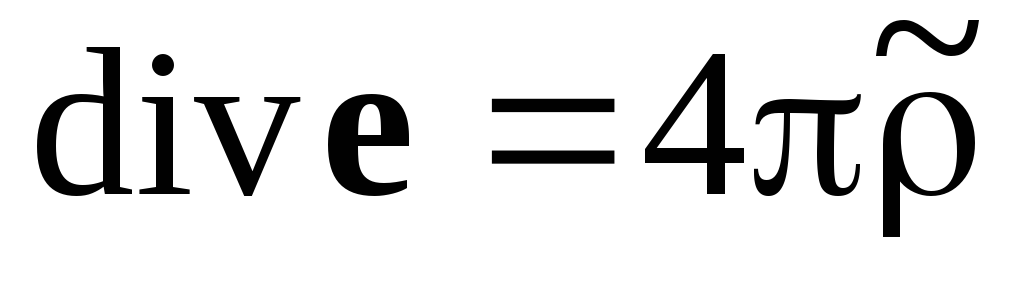 ,
(1.2) ,
(1.2)
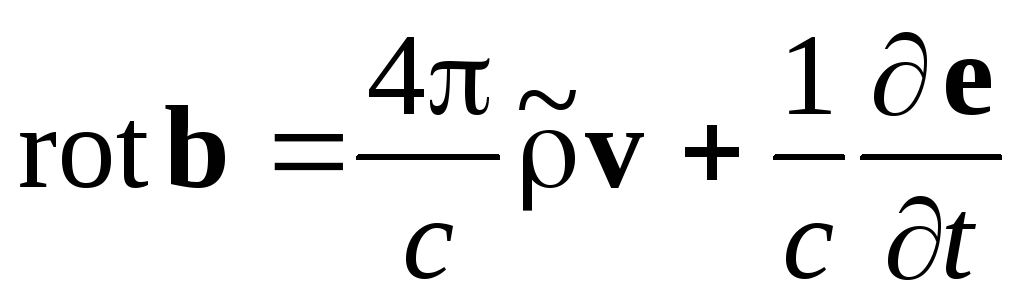 ,
(1.3) ,
(1.3)
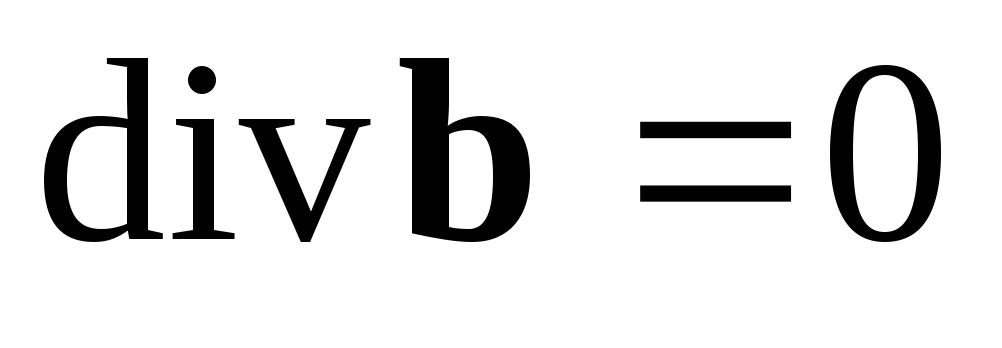 ,
(1.4) ,
(1.4)
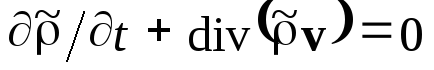 .
(1.5) Входящие в эти уравнения
величины .
(1.5) Входящие в эти уравнения
величины
 и
и
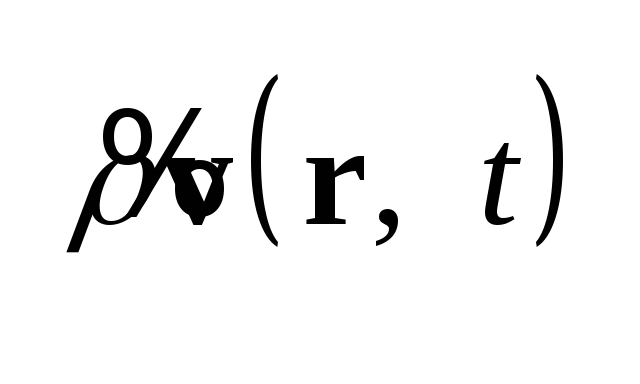 являются микроскопическими
значениями плотности
заряда и тока и связаны
с зарядами отдельных
микрочастиц среды
соотношениями:
являются микроскопическими
значениями плотности
заряда и тока и связаны
с зарядами отдельных
микрочастиц среды
соотношениями:
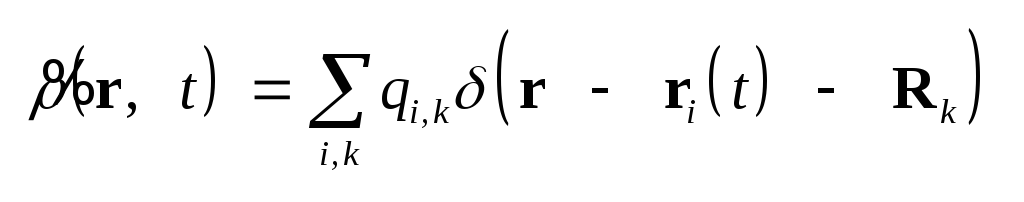 ,
(1.6) ,
(1.6)
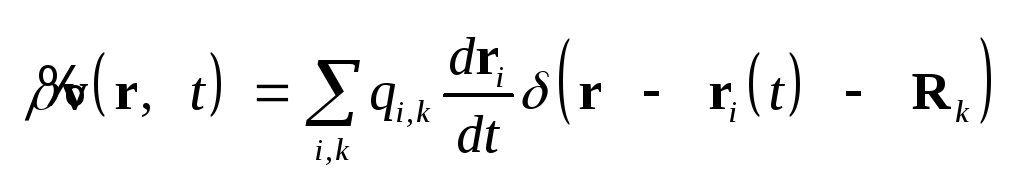 .
(1.7) .
(1.7)
|
1.2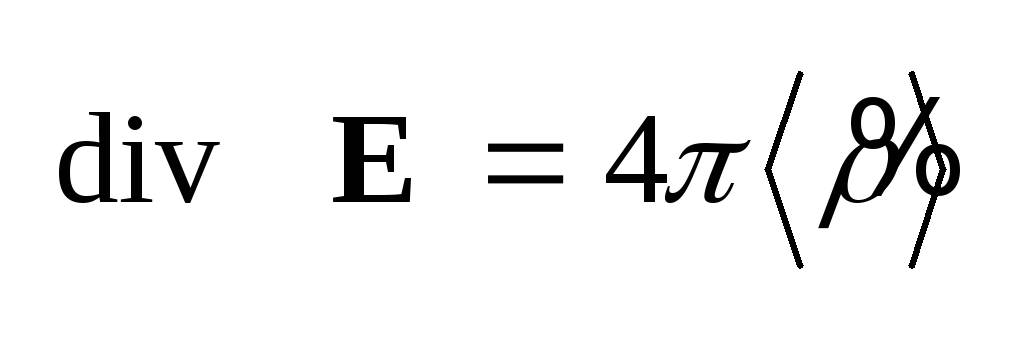 ,
(1.10) ,
(1.10)
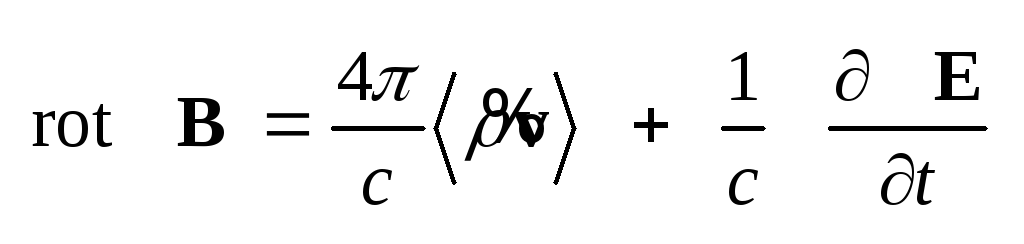 ,
(1.11) ,
(1.11)
 ,
(1.12) ,
(1.12)
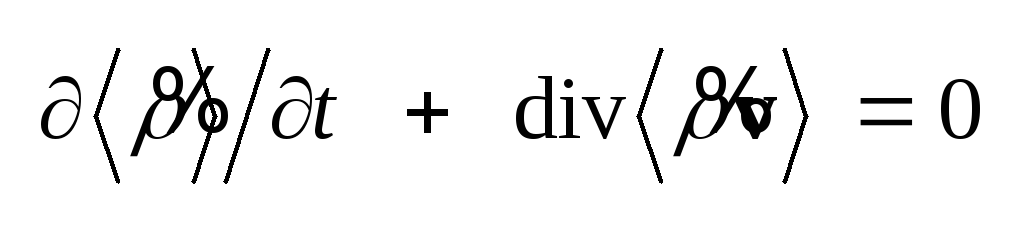 .
(1.13) Усреднение сглаживает
резкие колебания
микроскопических
величин, обусловленные
микроструктурой
вещества, и выявляет
средний ход их зависимости
от времени и координат,
характерный для сплошной
среды. Токи и заряды в
уравнениях (1.9) – (1.13) состоят,
вообще говоря, из двух
частей. Часть зарядов и
токов является функционалами
тех же самых полей Е
и В,
которые эти токи и заряды
в значительной степени
сами и определяют
(самосогласованные
поля). Такие заряды и токи
можно назвать внутренними
или собственными. Часть же
зарядов и токов может быть
обусловлена внешними
по отношению к данной
задаче причинами. Такие
заряды и токи, не зависящие
от Е
и В,
иногда называют сторонними
или внешними, то есть в уравнениях
(1.9) – (1.13) следует положить .
(1.13) Усреднение сглаживает
резкие колебания
микроскопических
величин, обусловленные
микроструктурой
вещества, и выявляет
средний ход их зависимости
от времени и координат,
характерный для сплошной
среды. Токи и заряды в
уравнениях (1.9) – (1.13) состоят,
вообще говоря, из двух
частей. Часть зарядов и
токов является функционалами
тех же самых полей Е
и В,
которые эти токи и заряды
в значительной степени
сами и определяют
(самосогласованные
поля). Такие заряды и токи
можно назвать внутренними
или собственными. Часть же
зарядов и токов может быть
обусловлена внешними
по отношению к данной
задаче причинами. Такие
заряды и токи, не зависящие
от Е
и В,
иногда называют сторонними
или внешними, то есть в уравнениях
(1.9) – (1.13) следует положить
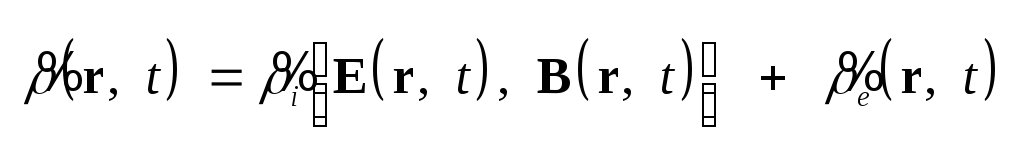 .
Собственные заряды в
веществе, в свою очередь,
можно разделить на свободные
и связанные (локализованные).
Свободными называют
заряды, которые могут
перемещаться на
макроскопические
расстояния. В отличие
от них связанные заряды
локализованы около
некоторых центров.
Примером свободных зарядов
могут служить электроны
проводимости в металле.
Связанными зарядами
в металле являются
электроны внутренних
оболочек атомов и .
Собственные заряды в
веществе, в свою очередь,
можно разделить на свободные
и связанные (локализованные).
Свободными называют
заряды, которые могут
перемещаться на
макроскопические
расстояния. В отличие
от них связанные заряды
локализованы около
некоторых центров.
Примером свободных зарядов
могут служить электроны
проводимости в металле.
Связанными зарядами
в металле являются
электроны внутренних
оболочек атомов и
|
1.3–
вектор с компонентами
di
= bxai/x
+ byai/y
+ bzai/z,
i
= x,
y,
z,
(векторный градиент).
Третье слагаемое в правой
части этого соотношения
может быть выражено через
производную плотности
квадрупольного момента.
Но квадрупольное слагаемое
содержит дополнительную
степень малой величины
|ri|/|r|
– отношения атомных
размеров к расстоянию,
на котором меняется
напряженность поля.
Следовательно, квадрупольная
поляризация среды мала,
и третьим слагаемым в
выражении для средней
плотности тока можно
пренебречь в сравнении
с первым. Второе слагаемое
в этом соотношении может
быть выражено через среднюю
плотность магнитного
момента вещества:
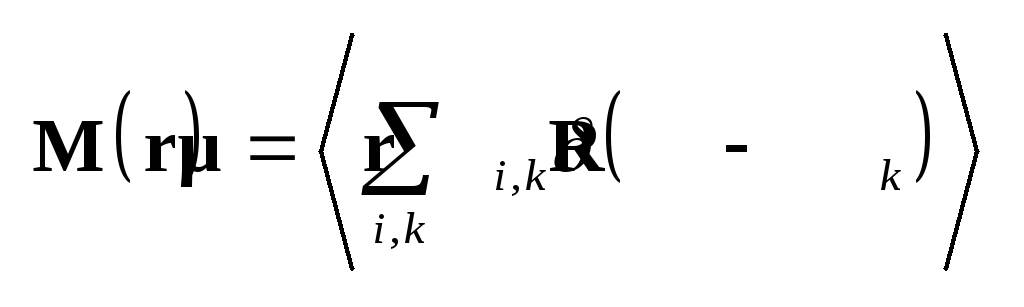 ,
(1.17) где ,
(1.17) где
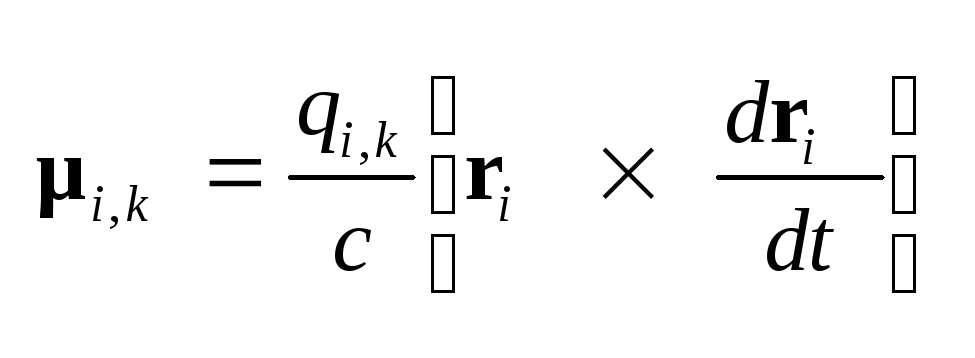 – магнитный момент, связанный
с движением i-го
заряда в k-м
атоме. С учетом этого выражение
для средней плотности тока
jл
связанных зарядов принимает
вид:
– магнитный момент, связанный
с движением i-го
заряда в k-м
атоме. С учетом этого выражение
для средней плотности тока
jл
связанных зарядов принимает
вид:
 .
(1.18) Первое слагаемое в
формуле (1.18) называется
током поляризации, а
второе – током намагничения,
то есть jp
= P/t,
jm
= c
rot
M.
В проводниках, содержащих
наряду со связанными и
свободные заряды, под
действием приложенного
поля возникает
макроскопическое
движение свободных зарядов,
то есть электрический
ток проводимости со средней .
(1.18) Первое слагаемое в
формуле (1.18) называется
током поляризации, а
второе – током намагничения,
то есть jp
= P/t,
jm
= c
rot
M.
В проводниках, содержащих
наряду со связанными и
свободные заряды, под
действием приложенного
поля возникает
макроскопическое
движение свободных зарядов,
то есть электрический
ток проводимости со средней
|
1.4
величин
Р
и М,
входящих в уравнения (1.22)
и (1.23), введем функции D
– вектор электрической
индукции и Н
– напряженность магнитного
поля: D
= Е
+ 4Р,
(1.24) Н
= В
– 4М.
(1.25) В этих обозначениях
уравнения (1.22) и (1.23) принимают
вид:
 ,
(1.26) ,
(1.26)
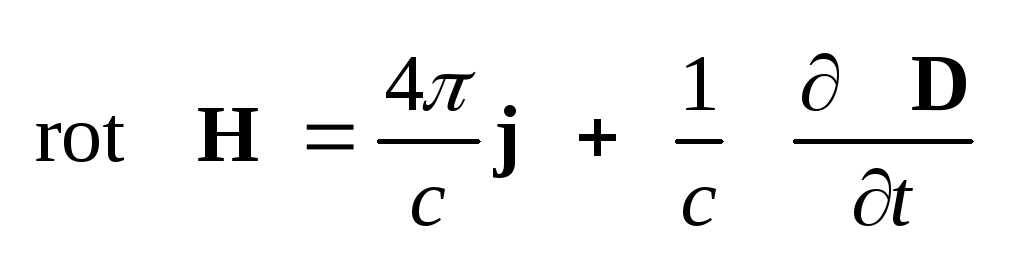 .
(1.27) Если тело не является
электронейтральным,
то есть в него введены извне
дополнительные
(сторонние) заряды, то к
плотности заряда
в уравнении (1.26) следует
добавить плотность сторонних
зарядов е,
а к плотности тока j
в уравнении (1.27) – плотность
тока сторонних зарядов
jе.
Таким образом, система
уравнений Максвелла,
описывающая поведение
электромагнитных полей
в веществе, принимает
вид: .
(1.27) Если тело не является
электронейтральным,
то есть в него введены извне
дополнительные
(сторонние) заряды, то к
плотности заряда
в уравнении (1.26) следует
добавить плотность сторонних
зарядов е,
а к плотности тока j
в уравнении (1.27) – плотность
тока сторонних зарядов
jе.
Таким образом, система
уравнений Максвелла,
описывающая поведение
электромагнитных полей
в веществе, принимает
вид:
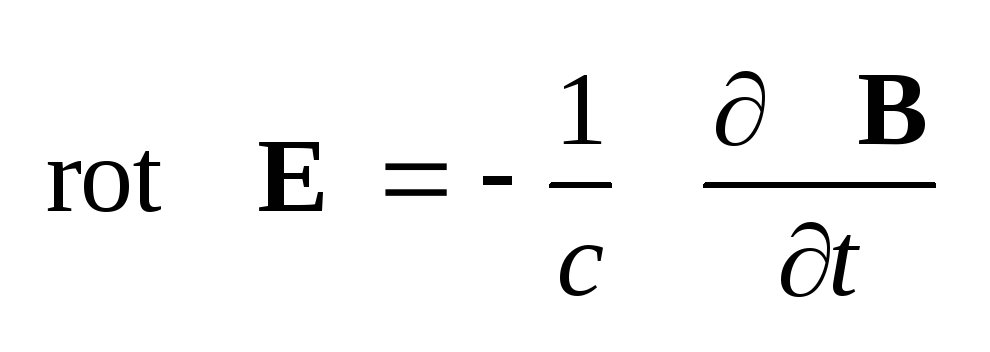 ,
(1.28) ,
(1.28)
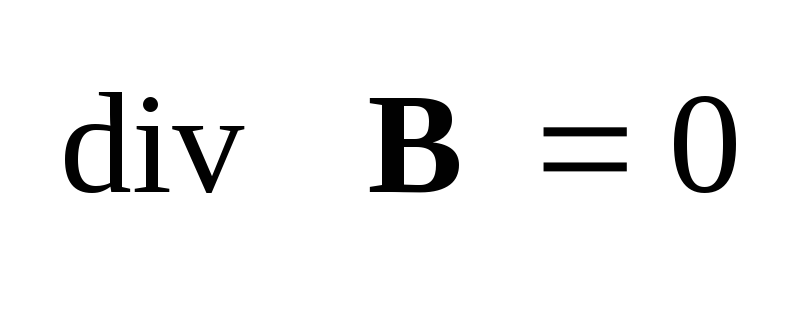 ,
(1.29) ,
(1.29)
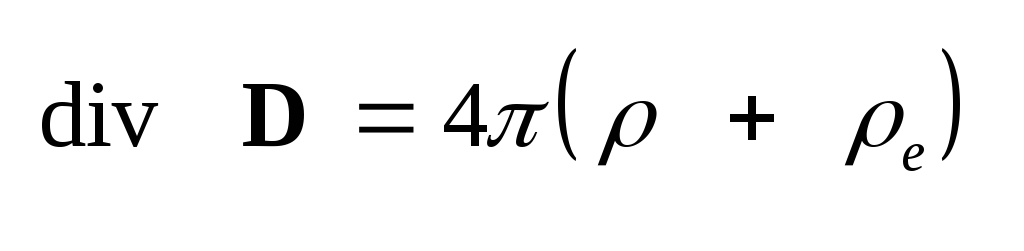 ,
(1.30) ,
(1.30)
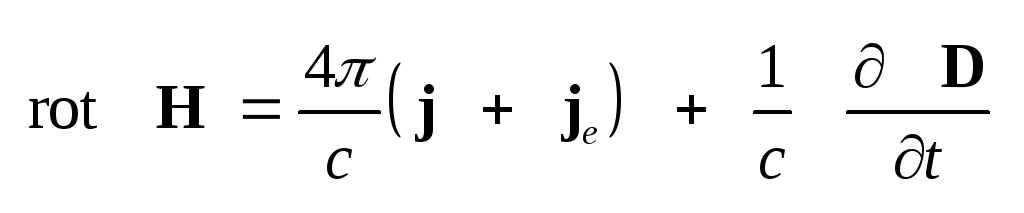 .
(1.31) Система этих уравнений
не является полной. К
ней нужно добавить
материальные уравнения,
связывающие величины
Р,
М
и j
с существующими
внутри тела макроскопическими
полями, а также граничные
условия, определяющие
поведение макроскопических
полей на границе раздела
различных сред. .
(1.31) Система этих уравнений
не является полной. К
ней нужно добавить
материальные уравнения,
связывающие величины
Р,
М
и j
с существующими
внутри тела макроскопическими
полями, а также граничные
условия, определяющие
поведение макроскопических
полей на границе раздела
различных сред.
|
|
|
2.1
Граничные условия При
микроскопическом
подходе такого понятия,
как граница раздела, не
существует, оно возникает
при рассмотрении вещества
как сплошной среды.
Микроскопическая
граница раздела представляет
собой некоторую область,
в которой свойства вещества
резко меняются. Для
конденсированных сред
толщина переходного
слоя порядка атомных размеров.
При макроскопическом
описании граница раздела
считается геометрической
поверхностью, то есть
предполагается, что при
переходе через некоторую
поверхность физические
свойства вещества
меняются скачком.
Формально переход к резкой
границе совершается
устремлением к нулю
толщины переходного
слоя. Если при этом в переходном
слое был конечный заряд,
то в результате такого
перехода он будет
сосредоточен на поверхности
раздела. Плотность
поверхностного заряда
связана с величиной q
заряда переходного
слоя соотношением
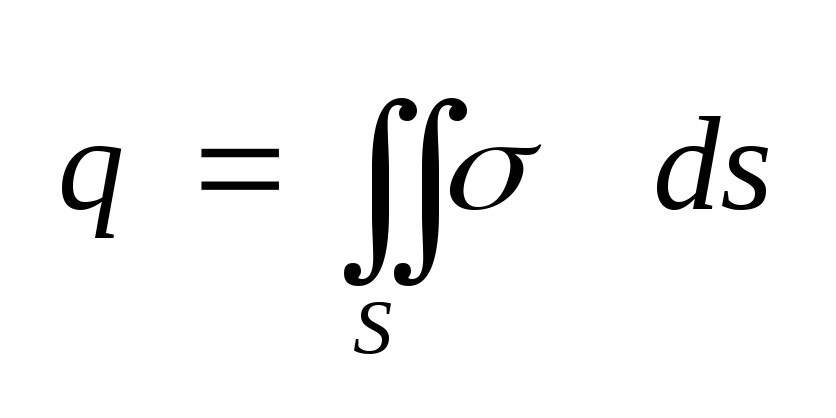 ,
ds
– элемент поверхности
раздела S.
Аналогично вводится
плотность поверхностного
тока i,
направление которого
совпадает с направлением
объемного тока j,
протекающего в
поверхностном слое. При
переходе к геометрической
поверхности раздела
величины Р
и М,
характеризующие
свойства вещества,
станут разрывными
функциями. Поэтому
удобно решать систему
уравнений для нахождения
макроскопических
электромагнитных полей
отдельно для каждого из
участков пространства,
занятого одним веществом.
На границах раздела сред
нужно производить
сшивание решений, используя
соответствующие
граничные условия.
Совокупность этих граничных
условий вытекает
непосредственно из
системы уравнений
Максвелла. Проинтегрируем, ,
ds
– элемент поверхности
раздела S.
Аналогично вводится
плотность поверхностного
тока i,
направление которого
совпадает с направлением
объемного тока j,
протекающего в
поверхностном слое. При
переходе к геометрической
поверхности раздела
величины Р
и М,
характеризующие
свойства вещества,
станут разрывными
функциями. Поэтому
удобно решать систему
уравнений для нахождения
макроскопических
электромагнитных полей
отдельно для каждого из
участков пространства,
занятого одним веществом.
На границах раздела сред
нужно производить
сшивание решений, используя
соответствующие
граничные условия.
Совокупность этих граничных
условий вытекает
непосредственно из
системы уравнений
Максвелла. Проинтегрируем,
|
2.2,
или (H1
– H2)
= 4in1/c,
где
= l/l
– единичный вектор,
касательный к границе
раздела. Это равенство
можно записать в векторном
виде, не зависящем явно
от выбора направления
касательной ,
вводя единичный вектор
нормали к поверхности
раздела n,
направленный из первой
среды во вторую: [n(H1
– H2)]
= 4i/c.
(1.33) Проинтегрируем
теперь уравнение (1.29)
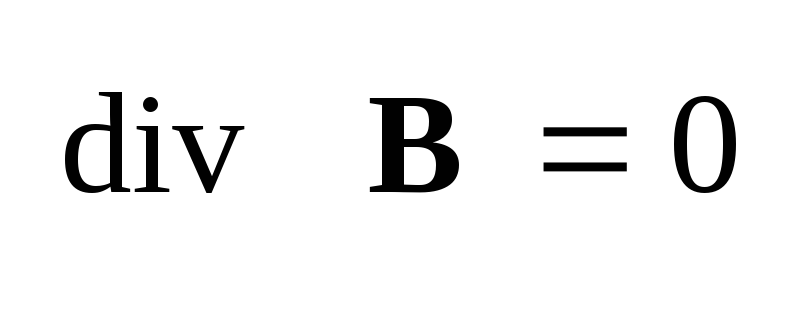 по
объему V
бесконечно малого
цилиндра, расположенного
в переходном слое так, что его
высота
есть толщина переходного
слоя, а основание площадью
S
параллельно возникающей
при
0 границе раздела. Используя
теорему о среднем и
теорему Гаусса –
Остроградского и переходя
к пределу
0, получим:
по
объему V
бесконечно малого
цилиндра, расположенного
в переходном слое так, что его
высота
есть толщина переходного
слоя, а основание площадью
S
параллельно возникающей
при
0 границе раздела. Используя
теорему о среднем и
теорему Гаусса –
Остроградского и переходя
к пределу
0, получим:
 ,
где Bn
– проекция вектора В
на нормаль n
к поверхности раздела.
Или: B1n
= B2n.
(1.34) Проинтегрировав по
этому же цилиндру уравнение
(1.30), ,
где Bn
– проекция вектора В
на нормаль n
к поверхности раздела.
Или: B1n
= B2n.
(1.34) Проинтегрировав по
этому же цилиндру уравнение
(1.30),
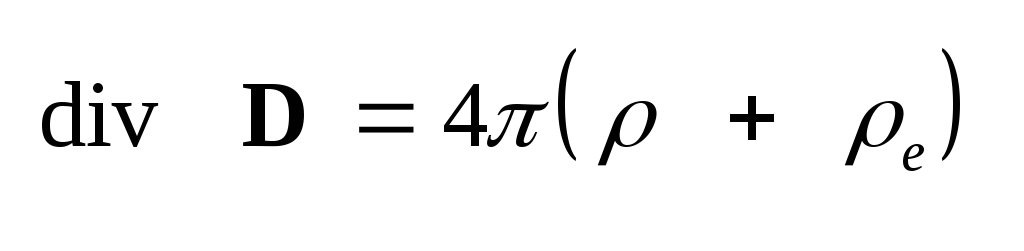 получаем:
получаем:
 .
То есть, D2n
– D1n
= 4. .
То есть, D2n
– D1n
= 4.
|
2.3Подставляя
в уравнение (1.36) формулы D
= Е
+ 4Р,
(1.24) Н
= В
– 4М.
(1.25): Di
= D0i
+ ikEk,
ik
=
ik
+ 4ik,
(1.37) Bi
= B0i
+ ikHk,
ik
= ik
+ 4ik,
(1.38) D0
= 4P0,
B0
= 4M0,
(1.39) где ik
и, ik
– тензоры диэлектрической
и магнитной проницаемости
вещества. ji
= ikEk,
(1.40) где ik
– тензор проводимости.
Соотношение (1.40) часто
называют законом Ома в
дифференциальной форме.
По принятой в макроскопической
электродинамике
классификации такие
токи являются сторонними,
их возникновение
описывается сторонней
силой fe
в правой части уравнения
(1.8). Соотношения (1.37) и (1.40)
являются материальными
уравнениями (уравнениями
связи) сплошной среды, они
устанавливают
необходимую связь различных
величин, характеризующих
макроскопическое
электромагнитное поле.
Эти связи содержат два
вектора и три тензораВ
частном случае изотропных
сред они принимают вид ik
=
ik,
ik
= ik,
ik
= ik.
Скалярные величины ,
и
называются диэлектрической
проницаемостью, магнитной
проницаемостью и
проводимостью вещества.
Величины Р0
и М0
в уравнении (1.39) представляют
собой плотности дипольных
электрического и
магнитного моментов
вещества при отсутствии
внешних полей. Их называют
спонтанными электрическим
и магнитным моментами
соответственно.
Вещества, для которых
Р0
0, называют пироэлектриками.
Для большинства веществ
Р0
= 0. Аналогично, для
большинства веществ, за
исключением
ферромагнетиков, М0
= 0. Все величины Р0,
М0,
ik
,
ik
и ik
для слабых постоянных или
медленно меняющихся
полей зависят только от
свойств вещества и его
термодинамического
состояния. При быстром
изменении полей величины
ik
,
ik
и ik
начинают зависеть от
частоты поля (дисперсия).
|
|
|
|
3.1
Обобщенная проницаемость
Разделение
средней плотности тока
связанных зарядов на токи
поляризации и токи
намагниченности, как
это сделано в формуле
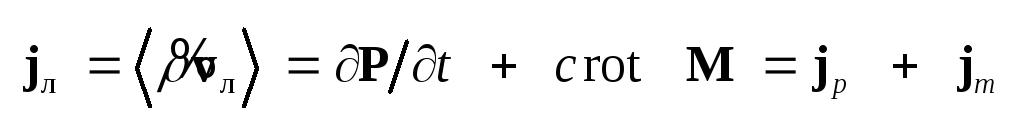 (1.18), является формальным.
Физически току
поляризации соответствует
колебание связанных
зарядов около положения
равновесия под действием
переменного электрического
поля, а току намагничения
– движение связанных
зарядов по замкнутым
траекториям даже в
отсутствии электрического
поля. Однако в переменном
поле траекторию движения
связанных зарядов можно
считать замкнутой лишь
приближенно, когда путь,
проходимый частицами
за период изменения
поля много больше радиуса
их траектории. В
быстропеременных полях
это условие не выполняется,
и отличить ток намагничения
от тока поляризации
невозможно. В такой
ситуации удобнее ввести
вектор обобщенной
поляризации P,
производная от которого
равняется средней плотности
микроскопического
тока:
(1.18), является формальным.
Физически току
поляризации соответствует
колебание связанных
зарядов около положения
равновесия под действием
переменного электрического
поля, а току намагничения
– движение связанных
зарядов по замкнутым
траекториям даже в
отсутствии электрического
поля. Однако в переменном
поле траекторию движения
связанных зарядов можно
считать замкнутой лишь
приближенно, когда путь,
проходимый частицами
за период изменения
поля много больше радиуса
их траектории. В
быстропеременных полях
это условие не выполняется,
и отличить ток намагничения
от тока поляризации
невозможно. В такой
ситуации удобнее ввести
вектор обобщенной
поляризации P,
производная от которого
равняется средней плотности
микроскопического
тока:
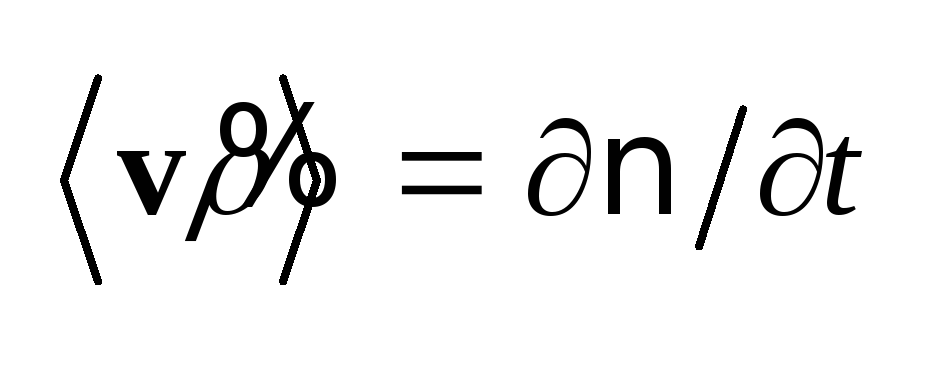 .
Из формулы (1.19) следует, что .
Из формулы (1.19) следует, что
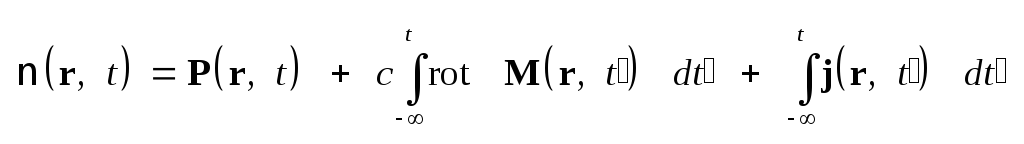 .
(1.41) Аналогично вводится
вектор D
обобщенной электрической
индукции: D(r,
t)
= E(r,
t)
+ 4P
(r,
t)
= .
(1.41) Аналогично вводится
вектор D
обобщенной электрической
индукции: D(r,
t)
= E(r,
t)
+ 4P
(r,
t)
=
 E(r,
t),
(1.42) где E(r,
t),
(1.42) где
 – линейный оператор
обобщенной проницаемости.
С учетом введенных обозначений
уравнения
– линейный оператор
обобщенной проницаемости.
С учетом введенных обозначений
уравнения
|
3.2Умножим
обе части уравнения (1.31)
скалярно на Е
и вычтем из полученного
выражения уравнение
(1.28), скалярно умноженное
на Н.
Учитывая, что тензоры
диэлектрической
и магнитной проницаемости
уравнениях (1.37) симметричные
и для медленно меняющихся
полей постоянные, получим:
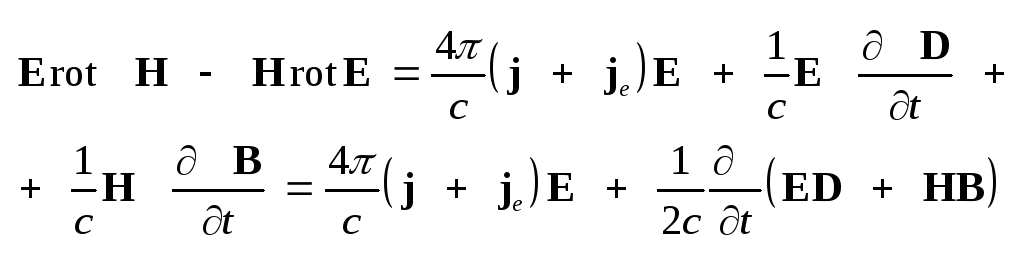 .
Воспользовавшись
тождеством div[ab]
= arotb
– brota,
преобразуем это уравнение
к виду: w/t
+ divS
= –(j
+ je)E,
(1.46) где с учетом соотношений
(1.37) обозначено .
Воспользовавшись
тождеством div[ab]
= arotb
– brota,
преобразуем это уравнение
к виду: w/t
+ divS
= –(j
+ je)E,
(1.46) где с учетом соотношений
(1.37) обозначено
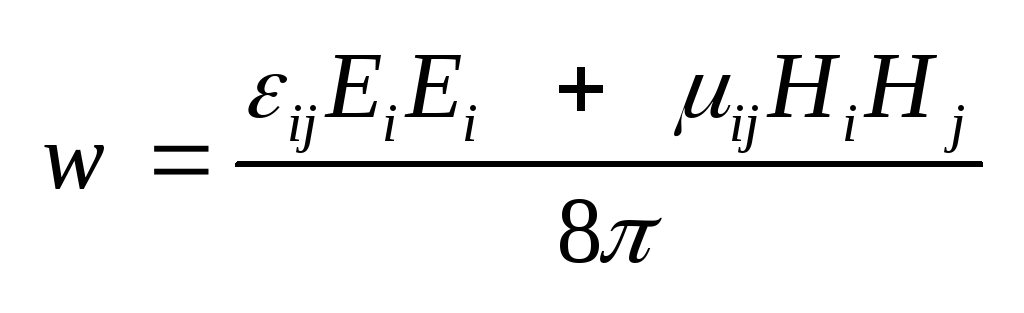 ,
(1.47) ,
(1.47)
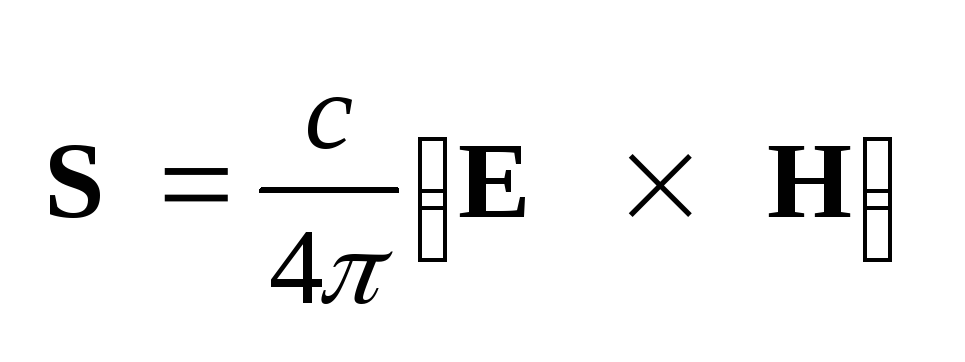 .
(1.48) В случае равенства
нулю правой части
соотношение (1.46) имеет
вид закона сохранения
некоторой физической
величины, причем w
имеет вид плотности этой
величины, а S
– плотности потока этой
величины. Энергия
электромагнитного
поля должна являться
термодинамическим
потенциалом, то есть быть
функцией состояния
системы и определяться
только текущими значениями
макроскопический
полей независимо от
предыстории. Кроме того,
энергия поля должна быть
разностью внутренней
энергии среды при наличии
поля и энергии в отсутствии
поля при тех же значениях
плотности и энтропии, а
изменение энергии поля
в обратимых процессах
должно равняться работе
внешних сил. .
(1.48) В случае равенства
нулю правой части
соотношение (1.46) имеет
вид закона сохранения
некоторой физической
величины, причем w
имеет вид плотности этой
величины, а S
– плотности потока этой
величины. Энергия
электромагнитного
поля должна являться
термодинамическим
потенциалом, то есть быть
функцией состояния
системы и определяться
только текущими значениями
макроскопический
полей независимо от
предыстории. Кроме того,
энергия поля должна быть
разностью внутренней
энергии среды при наличии
поля и энергии в отсутствии
поля при тех же значениях
плотности и энтропии, а
изменение энергии поля
в обратимых процессах
должно равняться работе
внешних сил.
|
|
|
|
|
4.1
Преобразования Лоренца
Рассмотрим
микроскопические
уравнения Максвелла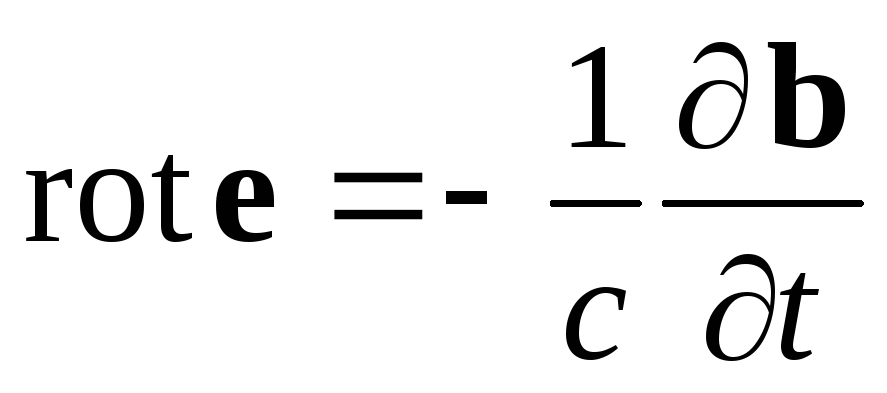 ,
(1.1) ,
(1.1)
 ,
(1.2) ,
(1.2)
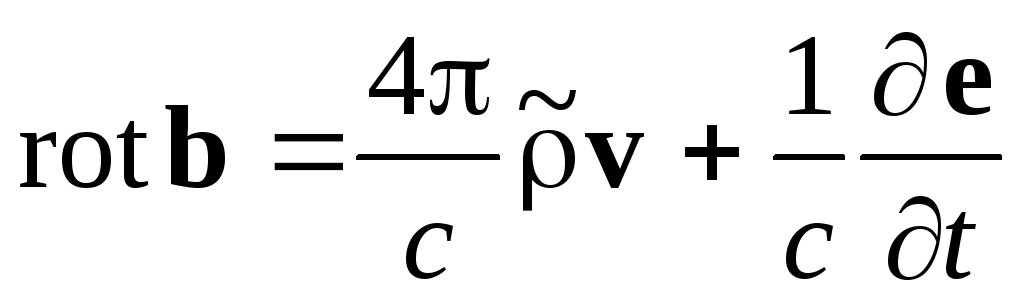 ,
(1.3) ,
(1.3)
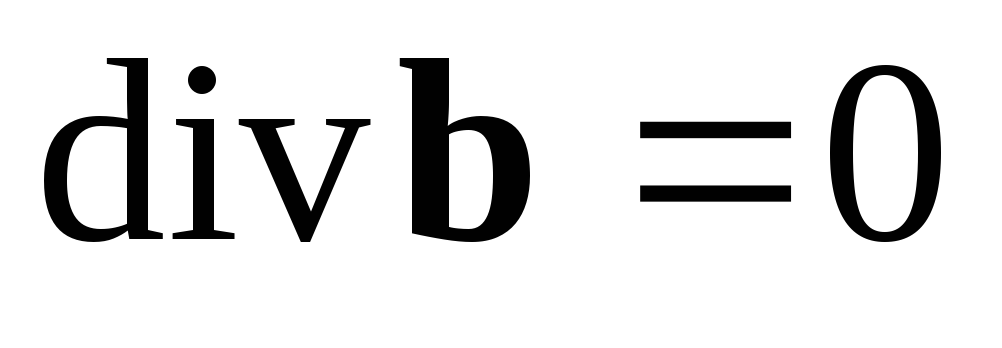 ,
(1.4) ,
(1.4)
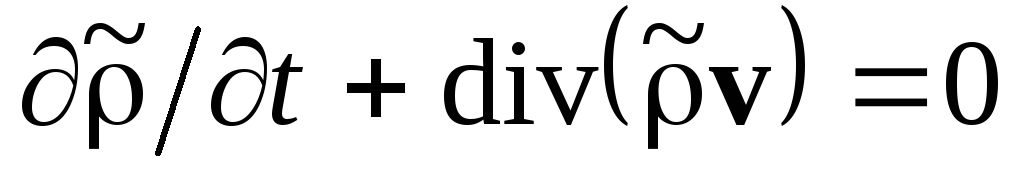 .
(1.5) в вакууме, то есть при .
(1.5) в вакууме, то есть при
 и
и
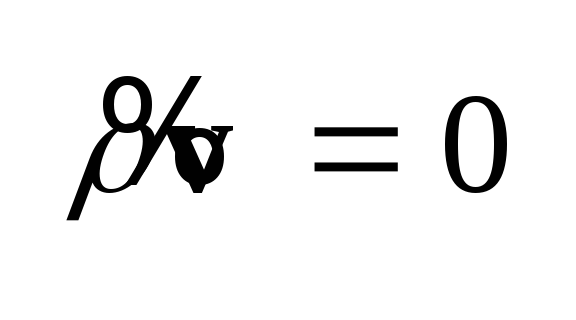 .
Возьмем ротор от уравнения
(1.1) и подставим в правую часть
уравнение (1.3). Тогда, с
учетом того, что в вакууме
из уравнения (1.2) следует
div
e
= 0, получаем волновое
уравнение .
Возьмем ротор от уравнения
(1.1) и подставим в правую часть
уравнение (1.3). Тогда, с
учетом того, что в вакууме
из уравнения (1.2) следует
div
e
= 0, получаем волновое
уравнение
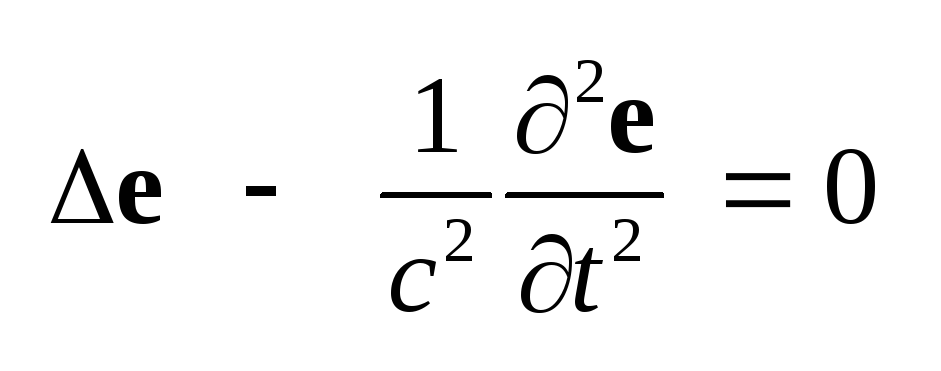 ,
(2.1) описывающее
распространение
электромагнитных волн
в пространстве со скоростью
с.
Первоначально предполагалось,
что волновое уравнение
(2.1) записано в «привилегированной»
системе отсчета,
связанной с неподвижным
мировым эфиром. Однако,
эксперименты (опыт
Майкельсона) показали,
что скорость света одинакова
во всех инерциальных системах
и во всех направлениях.
Это значит, что в сопутствующей
системе (r,
t)
волновое уравнение (2.1)
должно иметь такой же вид, что
и в лабораторной системе
(r,
t).
Легко видеть, что преобразование
Галилея ,
(2.1) описывающее
распространение
электромагнитных волн
в пространстве со скоростью
с.
Первоначально предполагалось,
что волновое уравнение
(2.1) записано в «привилегированной»
системе отсчета,
связанной с неподвижным
мировым эфиром. Однако,
эксперименты (опыт
Майкельсона) показали,
что скорость света одинакова
во всех инерциальных системах
и во всех направлениях.
Это значит, что в сопутствующей
системе (r,
t)
волновое уравнение (2.1)
должно иметь такой же вид, что
и в лабораторной системе
(r,
t).
Легко видеть, что преобразование
Галилея
|
4.2
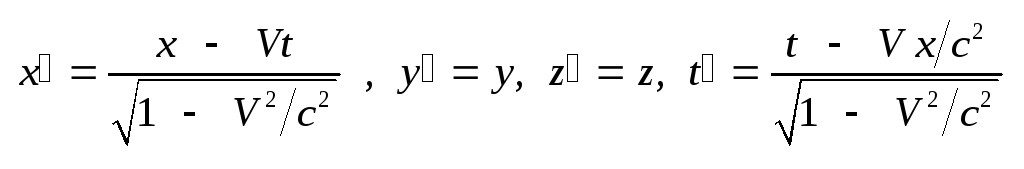 .
(2.3) Преобразование
Лоренца вида (2.3) легко
обобщить на случай произвольного
направления вектора
относительной скорости
V,
оно оставляет инвариантной
квадратичную форму
x2
+ y2
+ z2
– c2t2,
поэтому ему можно придать
геометрический смысл.
В 4-х мерном пространстве
(х1,
х2,
х3,
х4),
где х1
= х,
х2
= y,
х3
= z,
х4
= ict,
оно оставляет инвариантной
квадратичную форму .
(2.3) Преобразование
Лоренца вида (2.3) легко
обобщить на случай произвольного
направления вектора
относительной скорости
V,
оно оставляет инвариантной
квадратичную форму
x2
+ y2
+ z2
– c2t2,
поэтому ему можно придать
геометрический смысл.
В 4-х мерном пространстве
(х1,
х2,
х3,
х4),
где х1
= х,
х2
= y,
х3
= z,
х4
= ict,
оно оставляет инвариантной
квадратичную форму
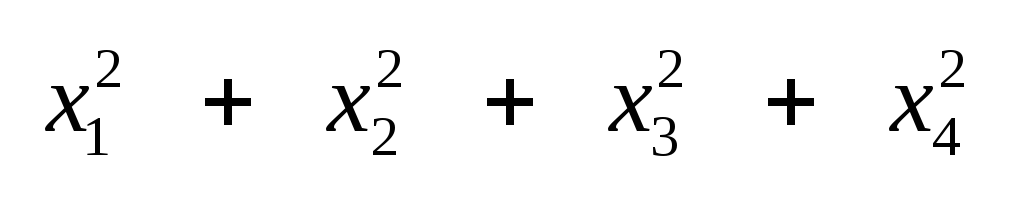 .
Поэтому преобразование
Лоренца соответствует
вращению системы
координат в рассматриваемом
4-пространстве, называемом
псевдоевклидовом
пространством Минковского,
и может быть записано в
матричном виде: .
Поэтому преобразование
Лоренца соответствует
вращению системы
координат в рассматриваемом
4-пространстве, называемом
псевдоевклидовом
пространством Минковского,
и может быть записано в
матричном виде:
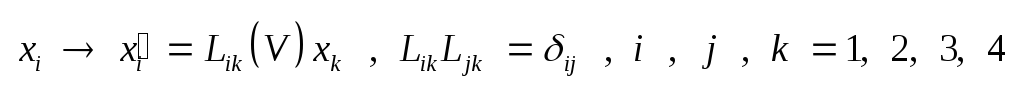 .
(2.4) Из формулы (2.3) вытекает
закон сложения скоростей: .
(2.4) Из формулы (2.3) вытекает
закон сложения скоростей:
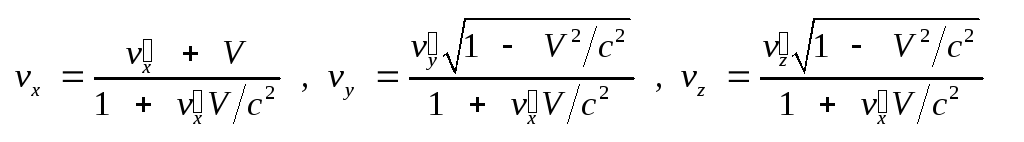 .
(2.5) Поскольку в силу принципа
относительности, сила,
действующая на движущийся
заряд должна быть одинакова
во всех инерциальных системах
отсчета, то при переходе
к движущейся системе
отсчета должно
преобразовываться и
электромагнитное поле.
Полагая, что в вакууме
сторонние силы fe
отсутствуют, запишем
уравнение .
(2.5) Поскольку в силу принципа
относительности, сила,
действующая на движущийся
заряд должна быть одинакова
во всех инерциальных системах
отсчета, то при переходе
к движущейся системе
отсчета должно
преобразовываться и
электромагнитное поле.
Полагая, что в вакууме
сторонние силы fe
отсутствуют, запишем
уравнение
|
4.3
пространстве
Минковского по формуле
(2.4):
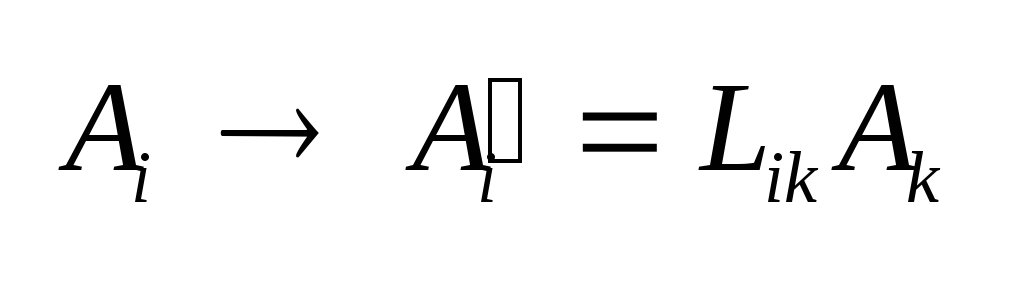 .
Преобразование Лоренца
вида (2.4) оставляет
инвариантом (скаляром)
величину .
Преобразование Лоренца
вида (2.4) оставляет
инвариантом (скаляром)
величину
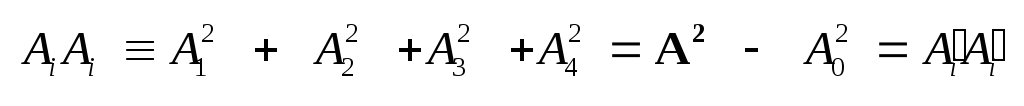 .
Здесь вектор А
объединяет три
пространственные
компоненты 4-вектора,
а A0
= A4/i
– его временная компонента.
Скалярное произведение
двух 4-векторов также
инвариантно при
преобразованиях
Лоренца: .
Здесь вектор А
объединяет три
пространственные
компоненты 4-вектора,
а A0
= A4/i
– его временная компонента.
Скалярное произведение
двух 4-векторов также
инвариантно при
преобразованиях
Лоренца:
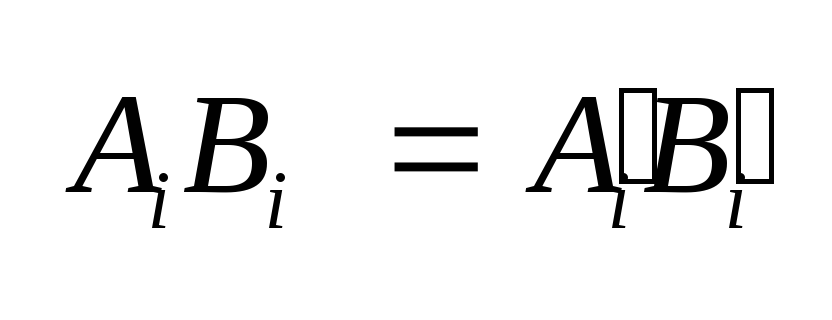 .
Существует и обратная
теорема: если АiBi
– скаляр, а Аi
– 4-вектор, то и Bi
– 4-вектор. На основании
этой теоремы, и учитывая,
что якобиан преобразования
Лоренца равен 1, можно
показать, что совокупность
величин ji
= {v,
ic}
образует 4-вектор
плотности тока. Отсюда
следует, что плотности
тока и заряда преобразуются
при переходе от одной
инерциальной системе
отсчета к другой по формулам,
аналогичным преобразованию
(2.3): .
Существует и обратная
теорема: если АiBi
– скаляр, а Аi
– 4-вектор, то и Bi
– 4-вектор. На основании
этой теоремы, и учитывая,
что якобиан преобразования
Лоренца равен 1, можно
показать, что совокупность
величин ji
= {v,
ic}
образует 4-вектор
плотности тока. Отсюда
следует, что плотности
тока и заряда преобразуются
при переходе от одной
инерциальной системе
отсчета к другой по формулам,
аналогичным преобразованию
(2.3):
 .
(2.8) 4-тензором второго ранга
называют упорядоченную
совокупность 16 величин
Tij,
преобразующуюся
при лоренцовом преобразовании
по закону: .
(2.8) 4-тензором второго ранга
называют упорядоченную
совокупность 16 величин
Tij,
преобразующуюся
при лоренцовом преобразовании
по закону:
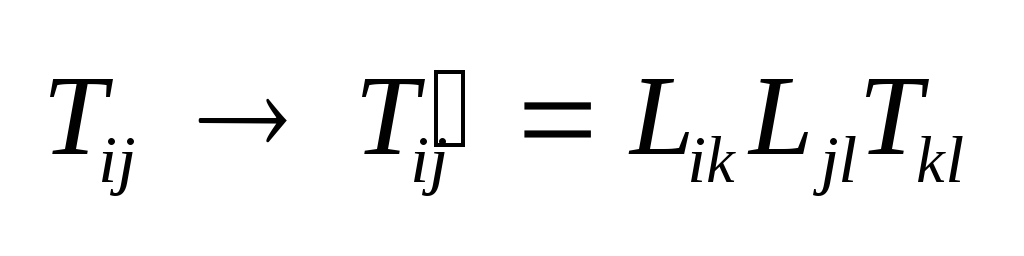 .
(2.9) В частности, 4-тензор
образуют величины
АiBj,
где Аi
и Bi
– произвольные 4-векторы.
Естественно, что при этом
Tii,
то есть сумма диагональных
компонент матрицы Tij
будет инвариантом при
лоренцовых преобразованиях.
Аналогично определяется
4-тензор третьего ранга как
упорядоченная совокупность
64 величин Tiik,
и т. д .
(2.9) В частности, 4-тензор
образуют величины
АiBj,
где Аi
и Bi
– произвольные 4-векторы.
Естественно, что при этом
Tii,
то есть сумма диагональных
компонент матрицы Tij
будет инвариантом при
лоренцовых преобразованиях.
Аналогично определяется
4-тензор третьего ранга как
упорядоченная совокупность
64 величин Tiik,
и т. д
|
4.4не
существует. Так, например,
импульс р
=
 и энергия
=
и энергия
=
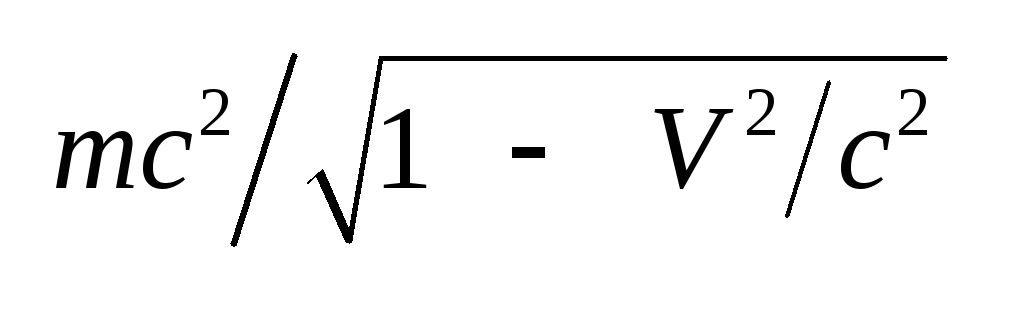 частицы с массой покоя
m
образуют 4-вектор
частицы с массой покоя
m
образуют 4-вектор
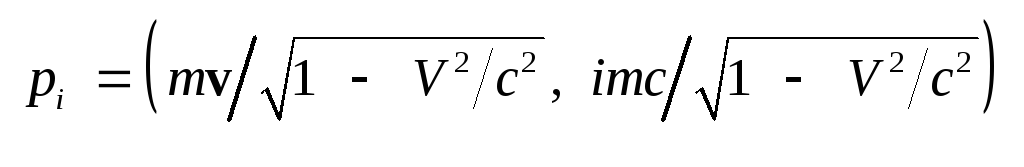 .
Установив, 4-вектором
или 4-тензором является
та или иная величина, мы, тем
самым задаем закон ее
преобразования в
инерциальных системах
отсчета. Физический
закон, связывающий 4-х
мерные величины, называется
ковариантным, если он
инвариантен относительно
преобразования Лоренца.
Уравнения Максвелла (1.1) и
(1.4) могут быть записаны в
ковариантной форме
через тензор электромагнитного
поля в виде .
Установив, 4-вектором
или 4-тензором является
та или иная величина, мы, тем
самым задаем закон ее
преобразования в
инерциальных системах
отсчета. Физический
закон, связывающий 4-х
мерные величины, называется
ковариантным, если он
инвариантен относительно
преобразования Лоренца.
Уравнения Максвелла (1.1) и
(1.4) могут быть записаны в
ковариантной форме
через тензор электромагнитного
поля в виде
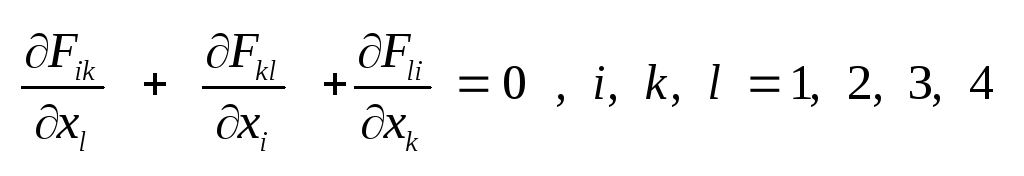 .
(2.13) Левая часть уравнения
(2.13) представляет собой
4-тензор третьего ранга и
его обращение в нуль не
зависит от выбора системы
отсчета. Аналогично
ковариантная форма
записи уравнений (1.2) и (1.3)
имеет вид: .
(2.13) Левая часть уравнения
(2.13) представляет собой
4-тензор третьего ранга и
его обращение в нуль не
зависит от выбора системы
отсчета. Аналогично
ковариантная форма
записи уравнений (1.2) и (1.3)
имеет вид:
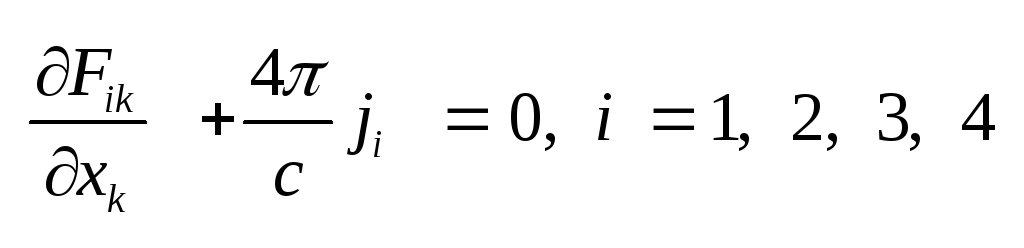 .
(2.14) .
(2.14)
|
|
|
|
|
|
4-х
мерной ковариантной
формой уравнений (1.30) и (1.31) в
среде:
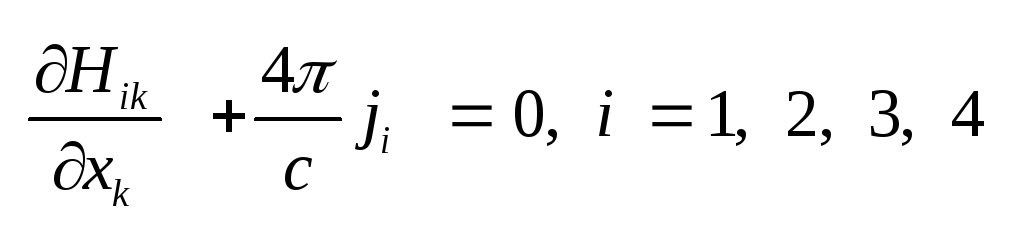 .
(2.16) 4-х вектор плотности
тока ji
= {j,
ic}
включает здесь как ток
проводимости, так и внешний
ток, соответственно, и
индуцированные и внешние
заряды. В случае однородного
и изотропного,
непироэлектрического
и неферромагнитного
тела можно записать D
= E,
B
= H.
Для того чтобы построить
связь между векторами
D,
H
и Е,
В
в лабораторной системе,
то есть для движущейся среды,
введем 4-вектор скорости,
связанный с трехмерной
скоростью v
соотношением .
(2.16) 4-х вектор плотности
тока ji
= {j,
ic}
включает здесь как ток
проводимости, так и внешний
ток, соответственно, и
индуцированные и внешние
заряды. В случае однородного
и изотропного,
непироэлектрического
и неферромагнитного
тела можно записать D
= E,
B
= H.
Для того чтобы построить
связь между векторами
D,
H
и Е,
В
в лабораторной системе,
то есть для движущейся среды,
введем 4-вектор скорости,
связанный с трехмерной
скоростью v
соотношением
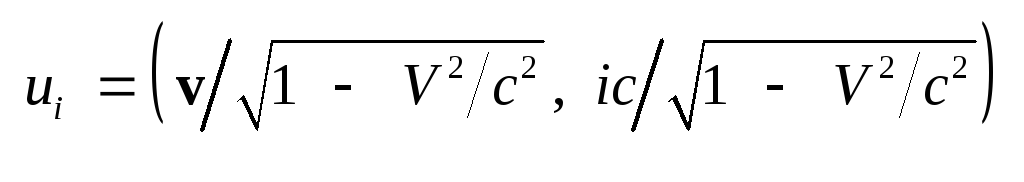 .
Нетрудно видеть, что
4-вектора Fikuk/c
и Нikuk/c
в неподвижной среде
переходят соответственно
в Е
и D,
так как их временные компоненты
при этом обращаются в нуль.
Поэтому 4-х мерным обобщением
равенства D
= E,
является уравнение Нikuk
= Fikuk.
(2.17) Аналогичным образом
можно убедиться, что 4-х
мерным обобщением равенства
B
= H
является уравнение Fikul
+ Fklui
+
Fliuk
= (Нikul
+ Hklui
+
Hliuk).
(2.18) Переходя от четырехмерных
обозначений снова к
трехмерным величинам,
получим из тензорных
уравнений (2.17) и (2.18) векторные
уравнения Минковского:
D
+ [VH]/c
= (E
+ [VB]/c),
(2.19) B
+ [EV]/c
= (H
+ [DV]/c).
(2.20) Считая отношение v/c
малым и решая эти уравнения
относительно D
и В,
получим с точностью до
членов первого порядка
малости: D
= E
+ (
– 1)[VH]/c,
(2.21) B
= H
+ (
– 1)[EV]/c.
(2.22) .
Нетрудно видеть, что
4-вектора Fikuk/c
и Нikuk/c
в неподвижной среде
переходят соответственно
в Е
и D,
так как их временные компоненты
при этом обращаются в нуль.
Поэтому 4-х мерным обобщением
равенства D
= E,
является уравнение Нikuk
= Fikuk.
(2.17) Аналогичным образом
можно убедиться, что 4-х
мерным обобщением равенства
B
= H
является уравнение Fikul
+ Fklui
+
Fliuk
= (Нikul
+ Hklui
+
Hliuk).
(2.18) Переходя от четырехмерных
обозначений снова к
трехмерным величинам,
получим из тензорных
уравнений (2.17) и (2.18) векторные
уравнения Минковского:
D
+ [VH]/c
= (E
+ [VB]/c),
(2.19) B
+ [EV]/c
= (H
+ [DV]/c).
(2.20) Считая отношение v/c
малым и решая эти уравнения
относительно D
и В,
получим с точностью до
членов первого порядка
малости: D
= E
+ (
– 1)[VH]/c,
(2.21) B
= H
+ (
– 1)[EV]/c.
(2.22)
|
Отметим,
что движущаяся среда
никак не меняет вида
микроскопических
уравнений поля. Такая среда
учитывается видом
плотности тока и плотности
заряда в уравнениях
(1.1) – (1.5). Характер усреднения
от движения среды тоже не
зависит, потому что
усреднение происходит
по объему и времени,
определенных по отношению
к лабораторной системе
координат. Следовательно,
уравнения Максвелла (1.28)
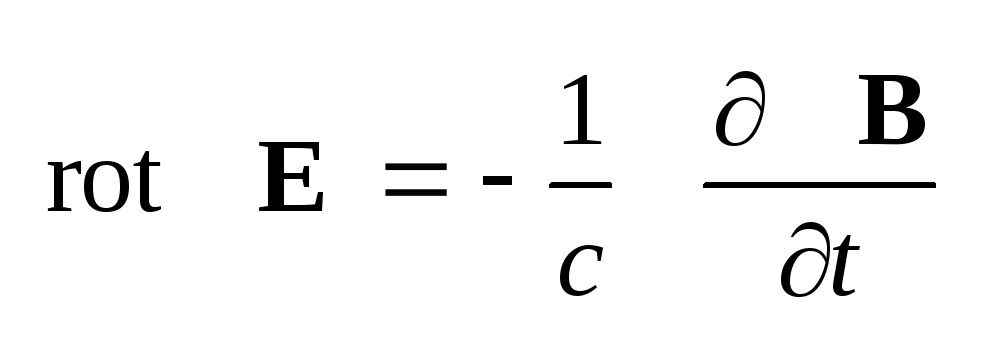 –
–
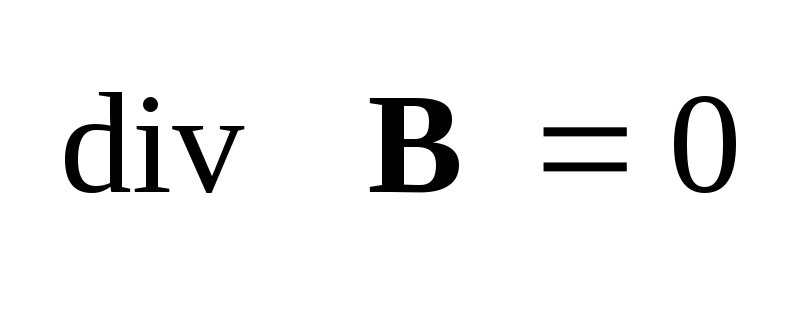 ,
(1.29) ,
(1.29)
 .
(1.31) для полей, записанных
по отношению к лабораторной
системе координат,
справедливы для движущейся
среды, так же как и для неподвижной,
поскольку при их выводе
использовались лишь такие
общие свойства тел, не
зависящее от движения,
как равенство нулю полного
заряда. Следует только
выяснить, как поведут себя
векторы D
и H
в случае движущейся среды.
Макроскопические
поля Е
и В
получены усреднением
соответствующих
микроскопических
полей, поскольку процедура
усреднения инвариантна
по отношению к преобразованиям
Лоренца, компоненты
полей Е
и В
образуют 4-тезор второго
ранга электромагнитного
поля Fik
вида .
(1.31) для полей, записанных
по отношению к лабораторной
системе координат,
справедливы для движущейся
среды, так же как и для неподвижной,
поскольку при их выводе
использовались лишь такие
общие свойства тел, не
зависящее от движения,
как равенство нулю полного
заряда. Следует только
выяснить, как поведут себя
векторы D
и H
в случае движущейся среды.
Макроскопические
поля Е
и В
получены усреднением
соответствующих
микроскопических
полей, поскольку процедура
усреднения инвариантна
по отношению к преобразованиям
Лоренца, компоненты
полей Е
и В
образуют 4-тезор второго
ранга электромагнитного
поля Fik
вида
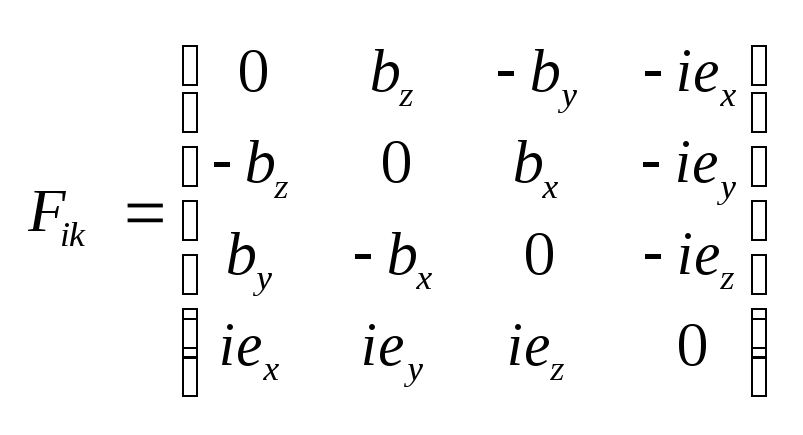 ,
(2.10) ,
(2.10)
|
|
|
|
тензоры
диэлектрической
и магнитной проницаемости
и проводимости
соответственно,
комплекснозначные
функции частоты.
Преобразование Фурье
от выражения (3.8) для обобщенной
индукции вычислим в
случае немагнитной среды
без пространственной
дисперсии, когда ij(t)
= ij(t).
Тогда
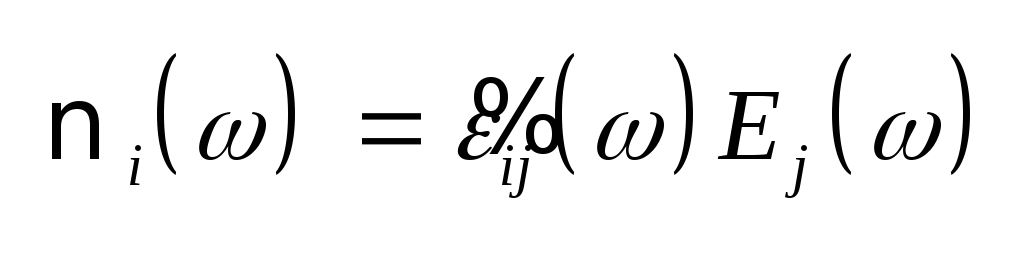 ,
(3.15) где ,
(3.15) где
 – (3.16) тензор комплексной
диэлектрической
проницаемости. Нетрудно
показать, исходя из
вещественности функций
отклика ij(t)
ij(t)
и ij(t),
что введенные соотношениями
(3.12), (3.13), (3.14) и (3.16) функции являются
эрмитово сопряженными,
то есть
– (3.16) тензор комплексной
диэлектрической
проницаемости. Нетрудно
показать, исходя из
вещественности функций
отклика ij(t)
ij(t)
и ij(t),
что введенные соотношениями
(3.12), (3.13), (3.14) и (3.16) функции являются
эрмитово сопряженными,
то есть
 , ,
 , ,
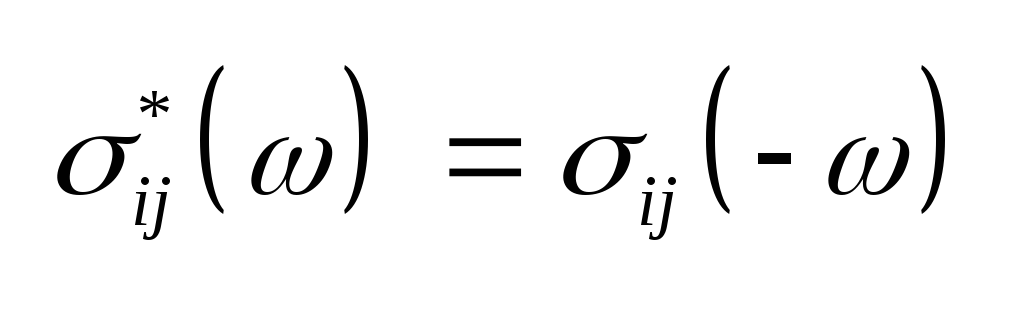 , ,
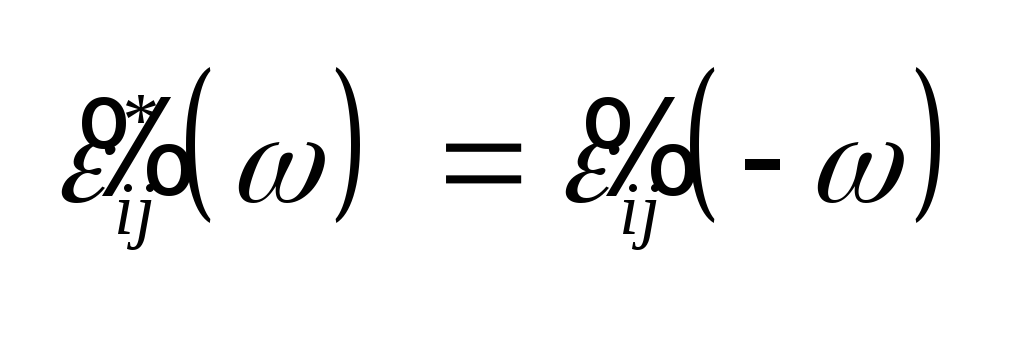 .
Следовательно, действительные
части проницаемостей
и проводимости – четные
функции частоты, а мнимые
– нечетные. .
Следовательно, действительные
части проницаемостей
и проводимости – четные
функции частоты, а мнимые
– нечетные.
|
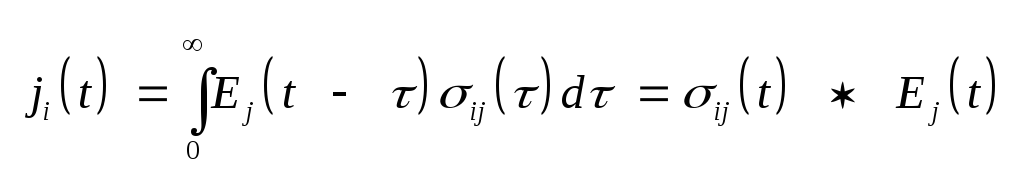 .
(3.7) Формула (3.4) для обобщенной
индукции с учетом соотношений
D
= Е
+ 4Р,
(1.24) Н
= В
– 4М.
(1.25) В этих обозначениях
уравнения (1.22) и (1.23) принимают
вид: , (1.31) .
(3.7) Формула (3.4) для обобщенной
индукции с учетом соотношений
D
= Е
+ 4Р,
(1.24) Н
= В
– 4М.
(1.25) В этих обозначениях
уравнения (1.22) и (1.23) принимают
вид: , (1.31)
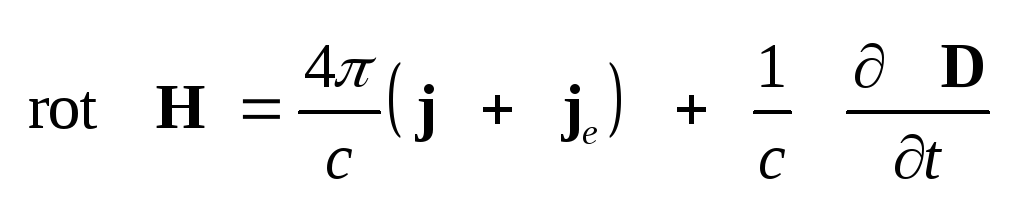 , ,
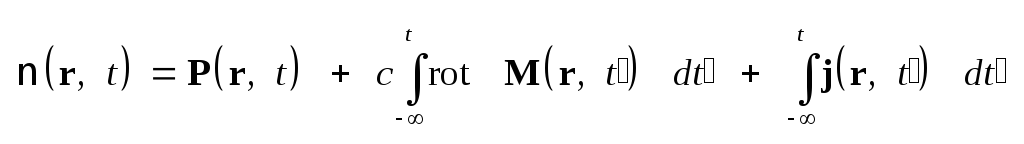 .
(1.41) , .
(1.41) ,
 .
(1.44) и выражений (3.5), (3.6) и (3.7)
для среды без пространственной
дисперсии принимает
вид: .
(1.44) и выражений (3.5), (3.6) и (3.7)
для среды без пространственной
дисперсии принимает
вид:
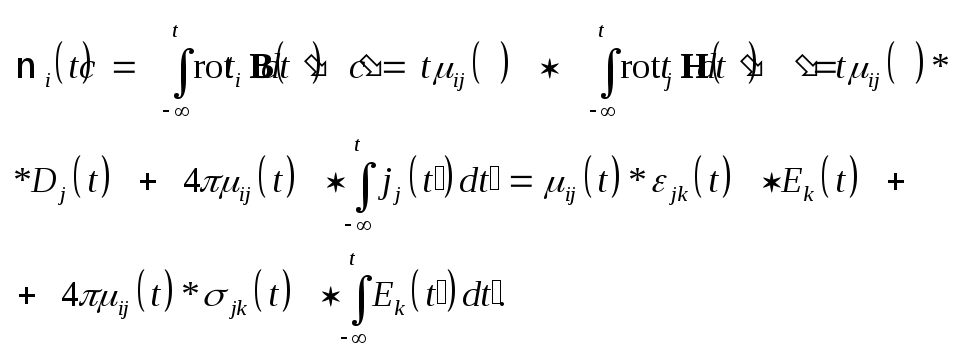 (3.8)
(3.8)
|
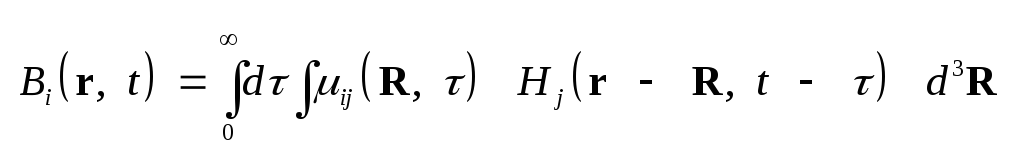 ,
(3.2) ,
(3.2)
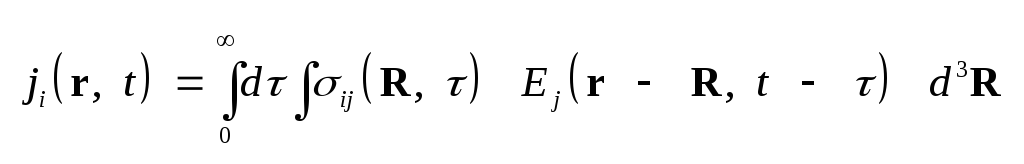 .
(3.3) Выражение (1.42) для обобщенной
индукции в случае
диспергирующей среды
может быть записано в виде .
(3.3) Выражение (1.42) для обобщенной
индукции в случае
диспергирующей среды
может быть записано в виде
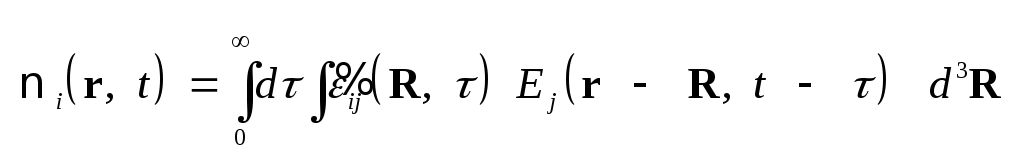 ,
(3.4) Пределы интегрирования
по времени в соотношениях
(3.1) – (3.4) отражают принцип
причинности: поляризация
и намагниченность среды
в данный момент времени не
могут зависеть от будущих
значений напряженности
поля. Зависимость реакции
среды от предшествующих
данному моменту значений
поля объясняется
конечностью времени
релаксации, то есть
перестройки, системы
зарядов. Фактически
память о предшествующих
значениях поля сохраняется
в течение конечного
времени, порядка времени
релаксации р
зарядов среды. Поэтому
функции отклика среды
ij(),
ij(),
ij()
быстро затухают при
> р.
Физическая причина
зависимости поляризации
или индуцированного
тока в точке наблюдения
r
от значения поля в соседних
точках пространства
r1
связана, например, с тем,
что в данную точку вследствие
теплового движения
могут приходить частицы
из соседних областей
пространства с другими
значениями полей. В
результате связь между
реакцией системы и
напряженностью поля ,
(3.4) Пределы интегрирования
по времени в соотношениях
(3.1) – (3.4) отражают принцип
причинности: поляризация
и намагниченность среды
в данный момент времени не
могут зависеть от будущих
значений напряженности
поля. Зависимость реакции
среды от предшествующих
данному моменту значений
поля объясняется
конечностью времени
релаксации, то есть
перестройки, системы
зарядов. Фактически
память о предшествующих
значениях поля сохраняется
в течение конечного
времени, порядка времени
релаксации р
зарядов среды. Поэтому
функции отклика среды
ij(),
ij(),
ij()
быстро затухают при
> р.
Физическая причина
зависимости поляризации
или индуцированного
тока в точке наблюдения
r
от значения поля в соседних
точках пространства
r1
связана, например, с тем,
что в данную точку вследствие
теплового движения
могут приходить частицы
из соседних областей
пространства с другими
значениями полей. В
результате связь между
реакцией системы и
напряженностью поля
|
|
|
|
|
и
магнитной проницаемостей,
а также для проводимости,
хотя они применяются
редко:
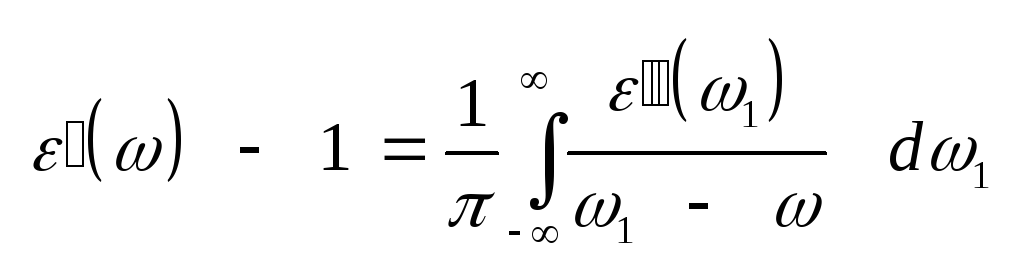 , ,
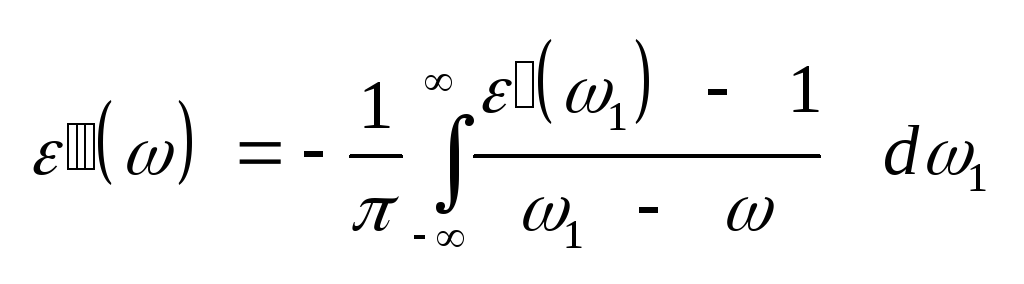 ,
(3.21) ,
(3.21)
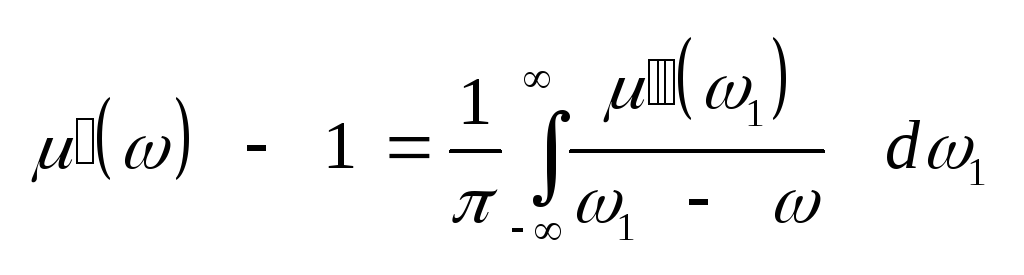 , ,
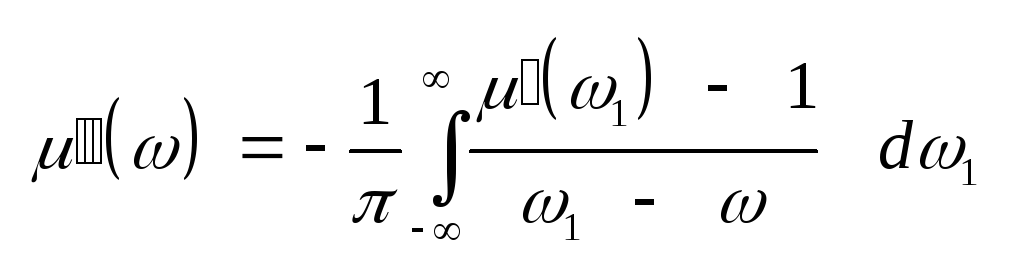 ,
(3.22) ,
(3.22)
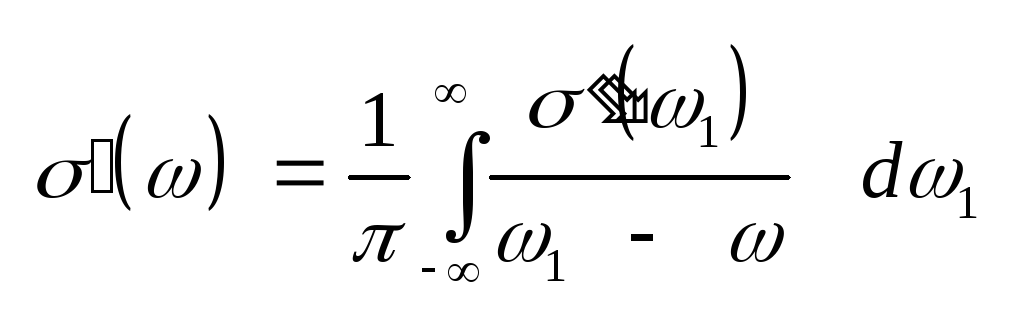 , ,
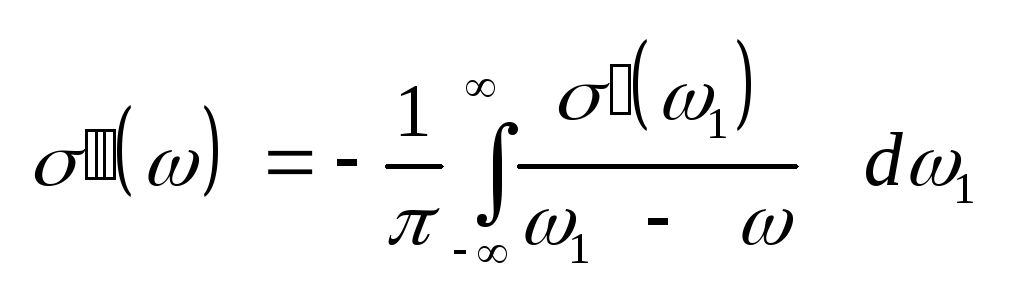 .
(3.23) Соотношения Крамерса
– Кронига (3.19) и (3.20), иногда
записывают так, Учитывая
четность функции ()
и нечетность функции (),
получим: .
(3.23) Соотношения Крамерса
– Кронига (3.19) и (3.20), иногда
записывают так, Учитывая
четность функции ()
и нечетность функции (),
получим:
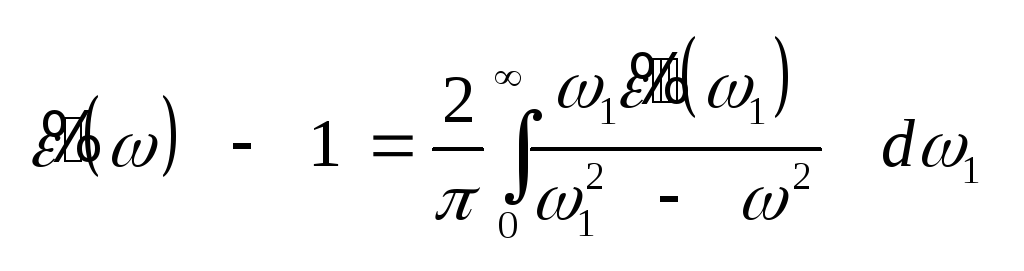 ,
(3.24) ,
(3.24)
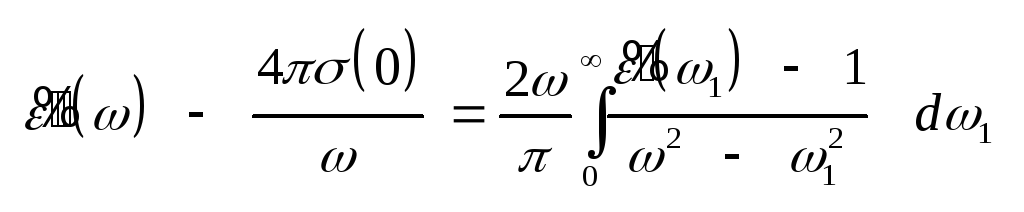 .
(3.25) .
(3.25)
|
(3.12)
принимает вид exp[(i
– )t].
Поскольку t
> 0, то множитель exp(–t)
при
> 0 обеспечивает быструю
сходимость интеграла.
Можно доказать, что функция
()
не имеет нулей в верхней
полуплоскости и
принимает там действительные
значения только на мнимой
полуоси
= i,
причем (i)
является монотонной
функцией. Из формулы
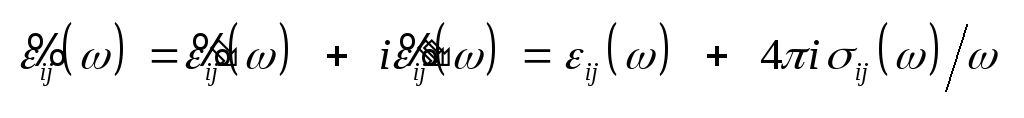 – (3.16) следует, что функция
– (3.16) следует, что функция
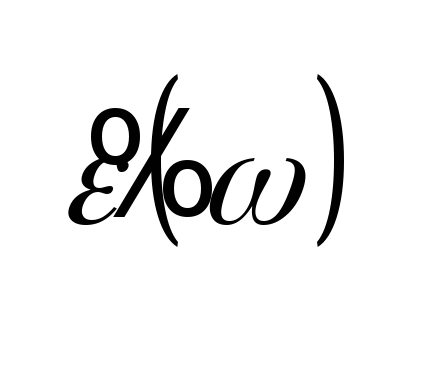 в верхней полуплоскости
имеет единственный полюс
= 0. Аналитичность функции
()
в верхней полуплоскости
комплексной переменной
=
+ i
означает, что действительная
и мнимая части диэлектрической
проницаемости не
являются независимыми.
Они связаны между собой
соотношениями Коши
– Римана:
в верхней полуплоскости
имеет единственный полюс
= 0. Аналитичность функции
()
в верхней полуплоскости
комплексной переменной
=
+ i
означает, что действительная
и мнимая части диэлектрической
проницаемости не
являются независимыми.
Они связаны между собой
соотношениями Коши
– Римана:
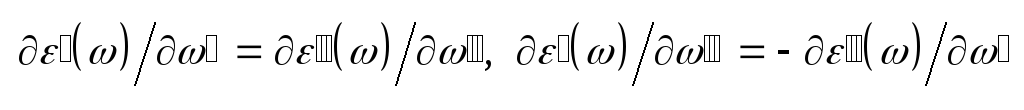 .
(3.18) На практике величины
и
обычно измеряют в
гармоническом режиме
как функции действительной
частоты, поэтому связь
между ними удобнее
записывать в виде интегралов
по действительным частотам.
Рассмотрим замкнутый
контуру C,
лежащий в верхней полуплоскости
и состоящий из дуг С1
и С2
радиусами R
и r
c центром в начале координат,
дуги С3
радиусом
r
c центром в точке 1
=
и отрезков действительной
оси, соединяющих эти дуги.
В силу теоремы Коши
интеграл от аналитической
функции по этому контуру
равен нулю, то есть .
(3.18) На практике величины
и
обычно измеряют в
гармоническом режиме
как функции действительной
частоты, поэтому связь
между ними удобнее
записывать в виде интегралов
по действительным частотам.
Рассмотрим замкнутый
контуру C,
лежащий в верхней полуплоскости
и состоящий из дуг С1
и С2
радиусами R
и r
c центром в начале координат,
дуги С3
радиусом
r
c центром в точке 1
=
и отрезков действительной
оси, соединяющих эти дуги.
В силу теоремы Коши
интеграл от аналитической
функции по этому контуру
равен нулю, то есть
|
|
|
|
(3.33)
Вычитая из Фурье-образа
уравнения
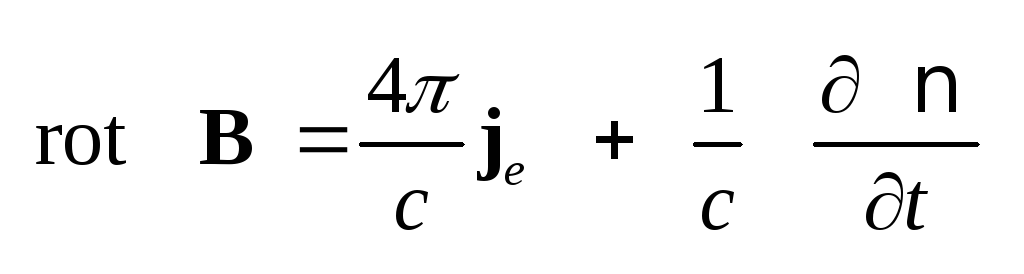 .
(1.44) .
(1.44)
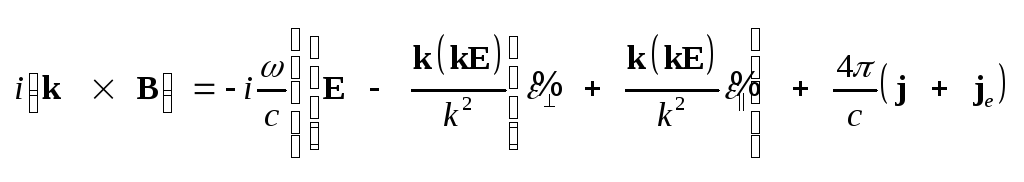 Фурье-образ уравнения
(1.31)
Фурье-образ уравнения
(1.31)
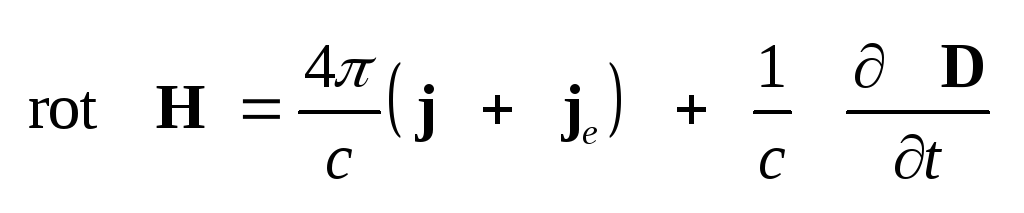
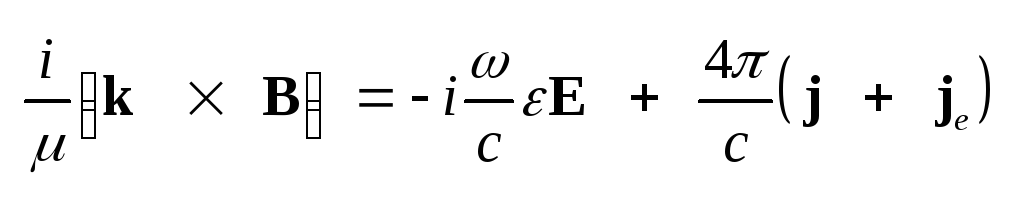 ,
видим, что i-я
компонента разностного
уравнения имеет вид ,
видим, что i-я
компонента разностного
уравнения имеет вид
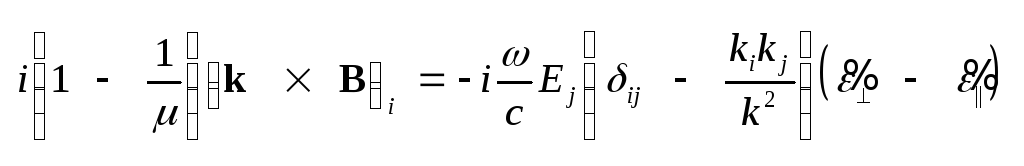 .
Выразим вектор В
в левой части этого
уравнения через вектор
Е
с помощью Фурье-образа
уравнения (1.28) .
Выразим вектор В
в левой части этого
уравнения через вектор
Е
с помощью Фурье-образа
уравнения (1.28)
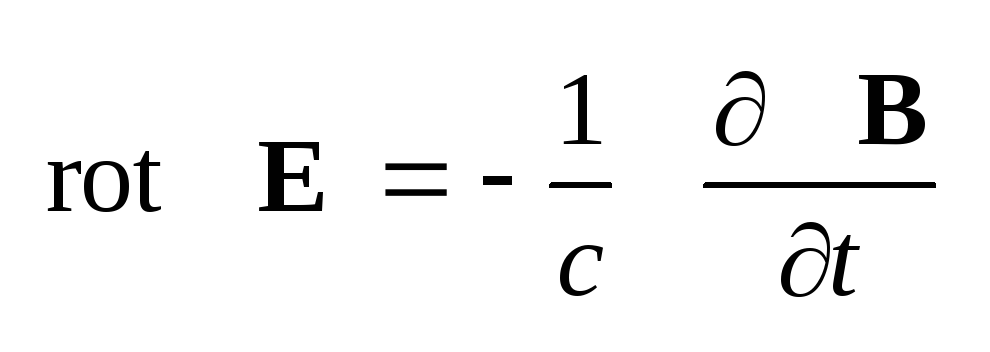 [k
E]
= B/c.
Раскрывая
[k
E]
= B/c.
Раскрывая
|
Насколько
пространственная
дисперсия существенна,
определяется параметром
kl,
k
= |k|
– волновое число, l
– характерный
пространственный масштаб
движения частиц среды,
в качестве которого
может выступать длина
свободного пробега
носителей заряда в
твердом теле или плазме,
размер куперовской пары
в сверхпроводнике и т. д.
Значение l
может быть порядка размера
структурных элементов
среды или пути, проходимого
частицами среды за
период изменения поля.
Пространственную
дисперсию необходимо
учитывать, если kl
1. Это условие означает,
что частицы движутся в
существенно неоднородном
поле. При наличии
пространственной
дисперсии диэлектрическая
проницаемость оказывается
тензором, а не скаляром
даже для изотропной среды.
Выделенное направление
в этом случае задает волновой
вектор k.
При отсутствии симметрии
возможен еще член с единичным
антисимметричным
тензором 3-го ранга eijk.
Поскольку компоненты
тензора 2-го ранга преобразуются
как произведения компонент
вектора, единственный
тензор 2-го ранга из компонент
волнового вектора
k
будет иметь вид kikj/k2.
Тогда
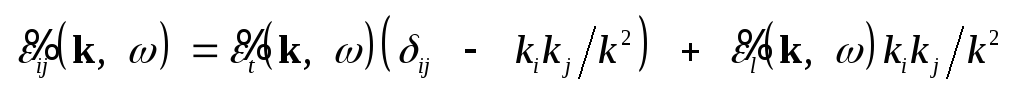 .
(3.31) Такой вид комплексной
диэлектрической
проницаемости означает,
что уравнение (3.29) может быть
записано в виде .
(3.31) Такой вид комплексной
диэлектрической
проницаемости означает,
что уравнение (3.29) может быть
записано в виде
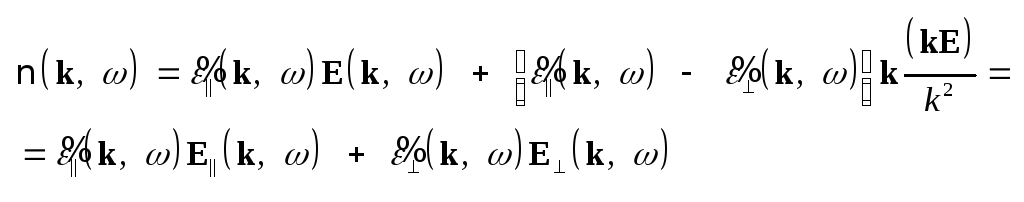 . .
|
Электрическое
поле E(r,
t)
можно представить в виде
4-мерного интеграла
Фурье (разложение по плоским
гармоническим волнам)
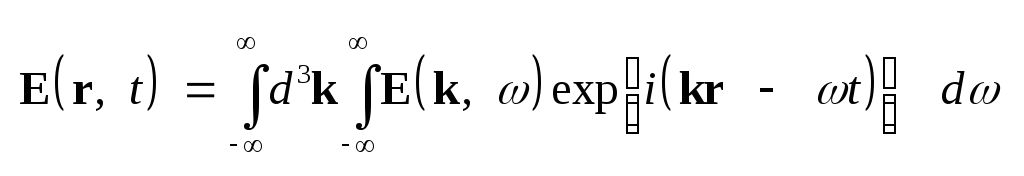 ,
(3.27) ,
(3.27)
 .
(3.28) Аналогично можно
определить D(k,
).
Взяв преобразование
Фурье вида (3.27) от правых и
левых частей уравнения
(3.4), получим с учетом известной
теоремы о спектре
свертки .
(3.28) Аналогично можно
определить D(k,
).
Взяв преобразование
Фурье вида (3.27) от правых и
левых частей уравнения
(3.4), получим с учетом известной
теоремы о спектре
свертки
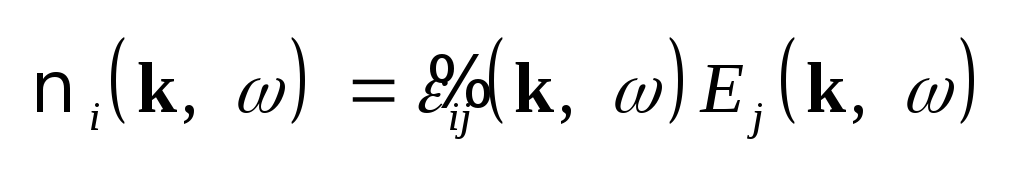 ,
(3.29) где тензор комплексной
диэлектрической
проницаемости, компоненты
которого зависят, в
общем случае, и от частоты,
и от волнового вектора,
для немагнитной среды в
силу соотношения (3.26) ,
(3.29) где тензор комплексной
диэлектрической
проницаемости, компоненты
которого зависят, в
общем случае, и от частоты,
и от волнового вектора,
для немагнитной среды в
силу соотношения (3.26)
 .
(3.30) Из определе .
(3.30) Из определе
|


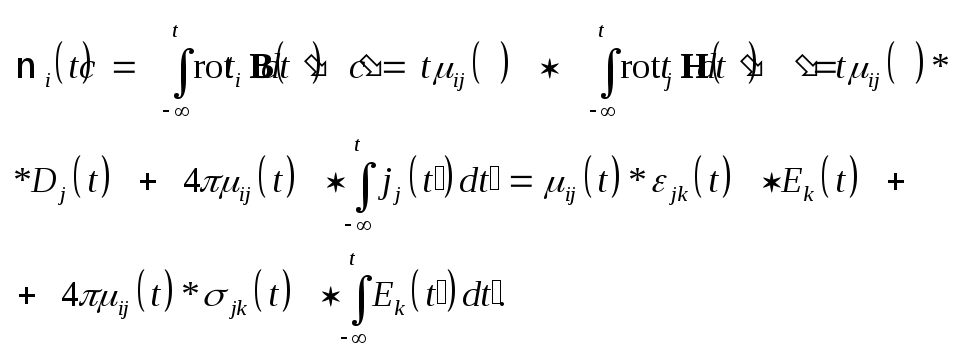 (3.8)
(3.8) .
(3.30) Из определе
.
(3.30) Из определе