|
9.1
Диссипация энергия
электромагнитного
поля в среде Частица
среды, двигаясь в переменном
электромагнитном поле,
получает от поля энергию,
при этом уменьшается энергия
электромагнитного
поля и растет механическая
энергия частицы. Поскольку
при перемещении частицы
генерируется поле,
то существует и обратный
процесс преобразования
механической энергии
частиц в энергию
электромагнитного
поля. Наличие такого
обмена энергией означает,
что в энергию электромагнитного
поля в среде следует
включать собственно энергию
микроскопического
поля, плотность которой в
соответствии с формулой
 ,
(1.47) равна (e2
+ b2)/8,
и энергию той части
механического
движения частиц среды,
которая обусловлена
электромагнитным полем
в среде. Частицы среды
вместе с взаимодействующим
с ними электромагнитным
полем не образуют замкнутую
систему. Они могут при
столкновениях передавать
свою энергию и импульс таким
возбуждениям среды,
которые уже непосредственно
не взаимодействуют
с полем и поэтому не
генерируют его. Такое
взаимодействие
описывается сторонними
силами fe
в микроскопическом
уравнении ,
(1.47) равна (e2
+ b2)/8,
и энергию той части
механического
движения частиц среды,
которая обусловлена
электромагнитным полем
в среде. Частицы среды
вместе с взаимодействующим
с ними электромагнитным
полем не образуют замкнутую
систему. Они могут при
столкновениях передавать
свою энергию и импульс таким
возбуждениям среды,
которые уже непосредственно
не взаимодействуют
с полем и поэтому не
генерируют его. Такое
взаимодействие
описывается сторонними
силами fe
в микроскопическом
уравнении
 .
(1.8). Часть энергии электромагнитного
поля при столкновениях
переходит в неупорядоченную
механическую энергию
частиц среды и не может
быть возвращена полю. Эта
энергия, в конечном счете,
переходит в тепло. Такой
процесс называется
диссипацией
энергии
электромагнитного
поля. .
(1.8). Часть энергии электромагнитного
поля при столкновениях
переходит в неупорядоченную
механическую энергию
частиц среды и не может
быть возвращена полю. Эта
энергия, в конечном счете,
переходит в тепло. Такой
процесс называется
диссипацией
энергии
электромагнитного
поля.
|
9.2
Операция
усреднения здесь весьма
существенна. Не усредненная
величина Ej
включает и ту энергию, которой
частицы обратимо
обмениваются с
электромагнитным полем,
и поэтому не описывает
диссипируемую энергию.
Если, как это удобно делать
для монохроматического
поля в линейной среде,
величины E
и D
считаются комплексными,
то
 .
Подставляя в эту формулу
выражение (3.29), получим: .
Подставляя в эту формулу
выражение (3.29), получим:
 .
(3.37) Здесь .
(3.37) Здесь
 , ,
 – (3.38) соответственно
эрмитова и антиэрмитова
части тензора комплексной
проницаемости. При этом
– (3.38) соответственно
эрмитова и антиэрмитова
части тензора комплексной
проницаемости. При этом
 .
Вообще, любой тензор может
быть представлен суммой
эрмитовой и антиэрмитовой
частей. Из соотношения
(3.37) следует, что в среде
поглощения нет, если тензор
комплексной диэлектрической
проницаемости не
содержит антиэрмитовой
части. Если диэлектрическая
проницаемость проводящего
немагнитного вещества
чисто действительный
тензор, то есть диэлектрические
потери отсутствуют,
то .
Вообще, любой тензор может
быть представлен суммой
эрмитовой и антиэрмитовой
частей. Из соотношения
(3.37) следует, что в среде
поглощения нет, если тензор
комплексной диэлектрической
проницаемости не
содержит антиэрмитовой
части. Если диэлектрическая
проницаемость проводящего
немагнитного вещества
чисто действительный
тензор, то есть диэлектрические
потери отсутствуют,
то
|
9.3
уравнение
Максвелла (1.28)
 для плоской гармонической
волны в изотропной среде
E(r,
t)
= Eexp(–it
+ ikr)
в виде [k
E]
= H/c.
(3.42 [k
E][k
E*]
= k2|E|2
– (kE)(kE*)
= (/c)2|H|2.
С учетом этой формулы
выражение (3.41) для плотности
мощности диссипации в
изотропной среде принимает
вид:
для плоской гармонической
волны в изотропной среде
E(r,
t)
= Eexp(–it
+ ikr)
в виде [k
E]
= H/c.
(3.42 [k
E][k
E*]
= k2|E|2
– (kE)(kE*)
= (/c)2|H|2.
С учетом этой формулы
выражение (3.41) для плотности
мощности диссипации в
изотропной среде принимает
вид:
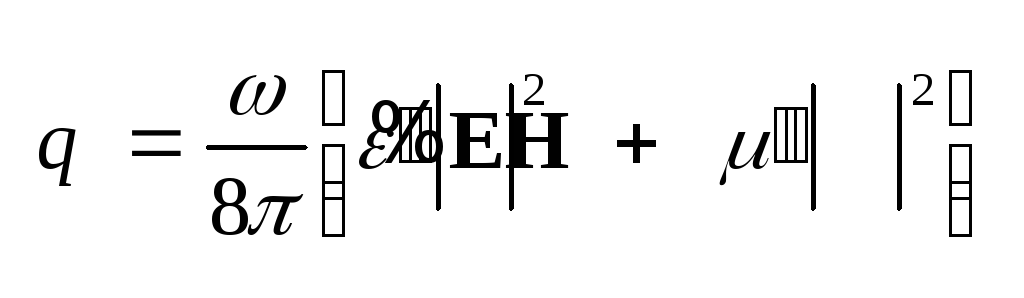 .
(3.43) Из формулы (3.43) следует,
что диссипация электромагнитной
энергии в среде определяется
мнимыми частями
диэлектрической
и магнитной проницаемостей.
Если ||
<< ||
и ||
<< ||,
то диссипация за период
поля мала по сравнению с
запасенной в веществе
электромагнитной
энергией. Области
частот, в которых
удовлетворяются эти
неравенства, называются
областями прозрачности
вещества Отметим, что в
формулу (3.43) входят комплексные
амплитуды электрического
и магнитного полей. Если
измеряются действительные
амплитуды полей E0
= Re(E)
и Н0
= Re(Н),
то, поскольку .
(3.43) Из формулы (3.43) следует,
что диссипация электромагнитной
энергии в среде определяется
мнимыми частями
диэлектрической
и магнитной проницаемостей.
Если ||
<< ||
и ||
<< ||,
то диссипация за период
поля мала по сравнению с
запасенной в веществе
электромагнитной
энергией. Области
частот, в которых
удовлетворяются эти
неравенства, называются
областями прозрачности
вещества Отметим, что в
формулу (3.43) входят комплексные
амплитуды электрического
и магнитного полей. Если
измеряются действительные
амплитуды полей E0
= Re(E)
и Н0
= Re(Н),
то, поскольку
 , ,
 ,
формулу (3.43) можно переписать
в виде ,
формулу (3.43) можно переписать
в виде
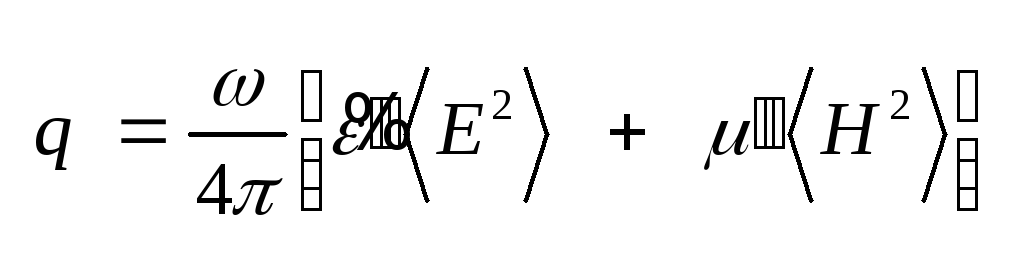 .
(3.45) .
(3.45)
|
|
|
|
10.1
Энергия электромагнитного
поля в диспергирующей
среде При
выводе уравнения Пойнтинга
w/t
+ divS
= –(j
+ je)E,
(1.46) предполагалась
мгновенная и локальная
связь между векторами
поля и индукции, что
справедливо только для
недиспергирующих
сред. Только в этом случае
величины
и
постоянны, и выражение
 ,
(1.47) является функцией
состояния. Кроме того,
выражения (1.47) и (1.48) были
отождествлены с
плотностью энергии и ее
потоком соответственно
на основании предположения,
что величина E(j
+ je)
равна работе электромагнитного
поля над заряженными
частицами среды. Это
утверждение также
справедливо не всегда.
Величина Eje
действительно равна
работе электромагнитного
поля над сторонними
зарядами, поскольку по
определению движение
сторонних зарядов не
зависит от микроскопического
поля. В общем случае работа
поля над средой в единицу
времени в единице объема
равна ,
(1.47) является функцией
состояния. Кроме того,
выражения (1.47) и (1.48) были
отождествлены с
плотностью энергии и ее
потоком соответственно
на основании предположения,
что величина E(j
+ je)
равна работе электромагнитного
поля над заряженными
частицами среды. Это
утверждение также
справедливо не всегда.
Величина Eje
действительно равна
работе электромагнитного
поля над сторонними
зарядами, поскольку по
определению движение
сторонних зарядов не
зависит от микроскопического
поля. В общем случае работа
поля над средой в единицу
времени в единице объема
равна
 .
Вычисление двух первых
слагаемых в правой части
этой формулы и выделение
из них диссипативной части
требует анализа
микроскопических
уравнений движения вида .
Вычисление двух первых
слагаемых в правой части
этой формулы и выделение
из них диссипативной части
требует анализа
микроскопических
уравнений движения вида
 .
(1.8). Аналогично плотность
энергии поля в среде как сумму
средних значений энергии
микроскопического
поля и механической
энергии индуцированных
зарядов следует .
(1.8). Аналогично плотность
энергии поля в среде как сумму
средних значений энергии
микроскопического
поля и механической
энергии индуцированных
зарядов следует
|
10.2Величина
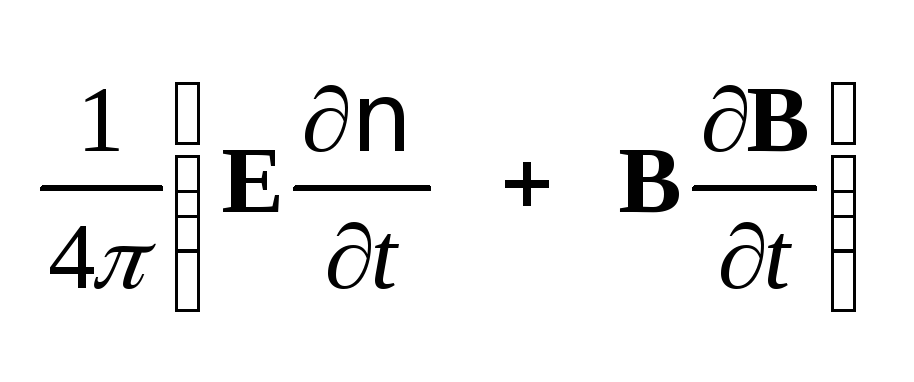 для диспергирующей
среды не является функцией
состояния, так как в силу
формулы (3.8) значение
обобщенной индукции
зависит от предшествующих
значений поля. Теорема
Пойнтинга (1.46) не содержит
никаких указаний на то, как
именно выражение в левой
части формулы (3.46) должно
делиться на части,
описывающие приращение
энергии поля в диспергирующей
среде, ее диссипацию и
поток. Такие указания
можно получить только
из материальных уравнений.
Однако, выражение работы
микроскопического
поля над частицами среды
через макроскопические
поле и плотность тока
индуцированных зарядов
требует анализа
микроскопических
уравнений движения. В
настоящее время не удается
получить общее решение
таких уравнений, выраженное
через феноменологическое
материальное уравнение
вида
для диспергирующей
среды не является функцией
состояния, так как в силу
формулы (3.8) значение
обобщенной индукции
зависит от предшествующих
значений поля. Теорема
Пойнтинга (1.46) не содержит
никаких указаний на то, как
именно выражение в левой
части формулы (3.46) должно
делиться на части,
описывающие приращение
энергии поля в диспергирующей
среде, ее диссипацию и
поток. Такие указания
можно получить только
из материальных уравнений.
Однако, выражение работы
микроскопического
поля над частицами среды
через макроскопические
поле и плотность тока
индуцированных зарядов
требует анализа
микроскопических
уравнений движения. В
настоящее время не удается
получить общее решение
таких уравнений, выраженное
через феноменологическое
материальное уравнение
вида
 .
Выражение для энергии
электромагнитного
поля в диспергирующей
среде можно получить
для случая слабой диссипации,
когда поле близко к
монохроматическому,
и его энергия на определенной
частоте велика в
сравнении с потерями в
среде. Для квазимонохроматических
полей E(r,
t)
= E0(r,
t)exp[i(kr
– t)],
B(r,
t)
= B0(r,
t)exp[i(kr
– t)]
комплексные амплитуды
E0(r,
t)
и B0(r,
t)
являются медленно
меняющимися функциями
координат и времени, то
есть |E0i|
<< k|E0|,
|E0i/t|
<< |E0|,
|B0i|
<< k|B0|,
|B0i/t|
<< |B0|.
(3.47) Условие малой диссипации
означает, что .
Выражение для энергии
электромагнитного
поля в диспергирующей
среде можно получить
для случая слабой диссипации,
когда поле близко к
монохроматическому,
и его энергия на определенной
частоте велика в
сравнении с потерями в
среде. Для квазимонохроматических
полей E(r,
t)
= E0(r,
t)exp[i(kr
– t)],
B(r,
t)
= B0(r,
t)exp[i(kr
– t)]
комплексные амплитуды
E0(r,
t)
и B0(r,
t)
являются медленно
меняющимися функциями
координат и времени, то
есть |E0i|
<< k|E0|,
|E0i/t|
<< |E0|,
|B0i|
<< k|B0|,
|B0i/t|
<< |B0|.
(3.47) Условие малой диссипации
означает, что
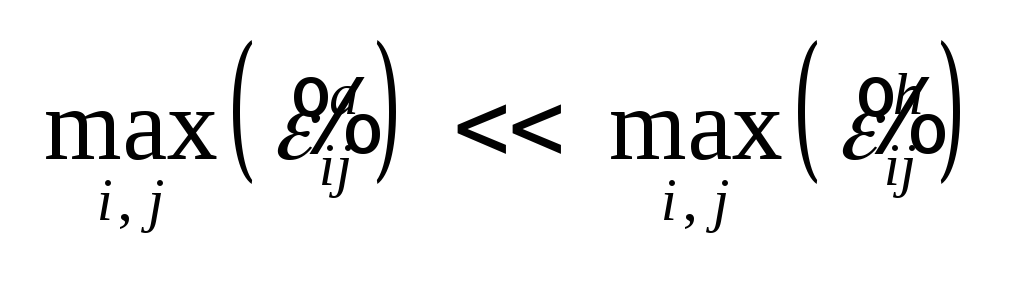 .
(3.48) Подставив в уравнение .
(3.48) Подставив в уравнение
|
10.3Пренебрегая
вторыми производными
ММА, получим:
 .(3.50)
Усредним уравнение (3.46) по
периоду Т
= 2/,
считая при этом медленно
меняющиеся амплитуды
постоянными. В левой
части уравнения (3.46)
действительные значения
поля и производной
обобщенной индукции возьмем
в виде .(3.50)
Усредним уравнение (3.46) по
периоду Т
= 2/,
считая при этом медленно
меняющиеся амплитуды
постоянными. В левой
части уравнения (3.46)
действительные значения
поля и производной
обобщенной индукции возьмем
в виде
 , ,
 .
Соответственно, с учетом
формулы (3.50) .
Соответственно, с учетом
формулы (3.50)
 .(3.51) .(3.51)
|
10.4.)
Здесь учтено, что среда
является пространственно
однородной. Третье
слагаемое формулы (3.51)
для стационарной среды
принимает вид:
 (3.54) Подставляя формулы
(3.51), (3.52), (3.53) и (3.54) в левую часть
усредненного по периоду
уравнения (3.46) и учитывая,
что
(3.54) Подставляя формулы
(3.51), (3.52), (3.53) и (3.54) в левую часть
усредненного по периоду
уравнения (3.46) и учитывая,
что
 , ,
 ,
получим: ,
получим:

|
10.5получаем
 .
Подставляя это соотношение
в формулу (3.56) и пренебрегая
,
получим: .
Подставляя это соотношение
в формулу (3.56) и пренебрегая
,
получим:
 ,
что совпадает с формулой
(1.47). Для диспергирующей
изотропной магнитной среды
из формул (3.35) и (3.56) аналогично
можно получить выражение
для средней за период плотности
энергии в виде: ,
что совпадает с формулой
(1.47). Для диспергирующей
изотропной магнитной среды
из формул (3.35) и (3.56) аналогично
можно получить выражение
для средней за период плотности
энергии в виде:
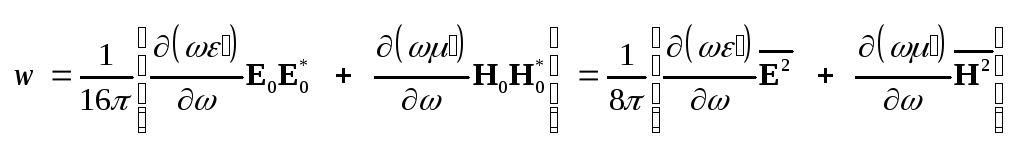 ,
(3.58 ,
(3.58
|
|
11.
1Электростатика
проводников В
диэлектриках нет
свободных зарядов, то есть
= 0, а распределение сторонних
зарядов e
задается внешними
условиями. Следовательно,
для диэлектрика система
стационарных уравнений
(1.28)
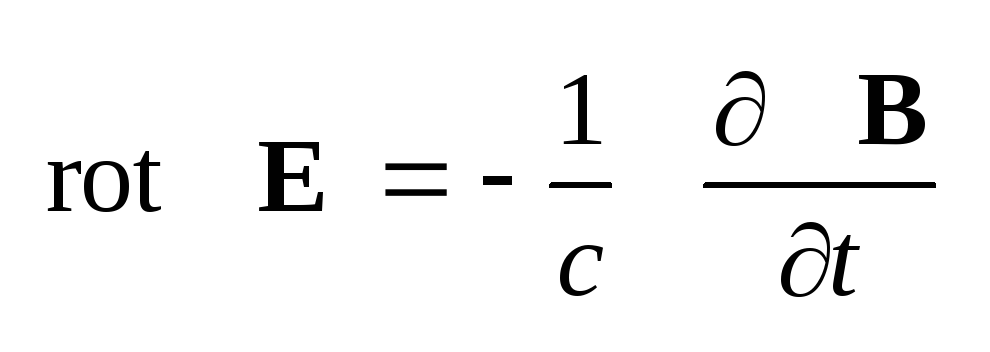 ,
(1.30) ,
(1.30)
 ,
(Di
= D0i
+ ikEk,
ik
=
ik
+ 4ik,
Di
= D0i
+ ikEk,
ik
=
ik
+ 4ik,
(1.37) ) является замкнутой.
Для проводников же плотность
свободных зарядов зависит
от напряженности поля
и не может быть задана
произвольно. Поэтому
систему уравнений
следует дополнить
уравнением непрерывности
,
(Di
= D0i
+ ikEk,
ik
=
ik
+ 4ik,
Di
= D0i
+ ikEk,
ik
=
ik
+ 4ik,
(1.37) ) является замкнутой.
Для проводников же плотность
свободных зарядов зависит
от напряженности поля
и не может быть задана
произвольно. Поэтому
систему уравнений
следует дополнить
уравнением непрерывности
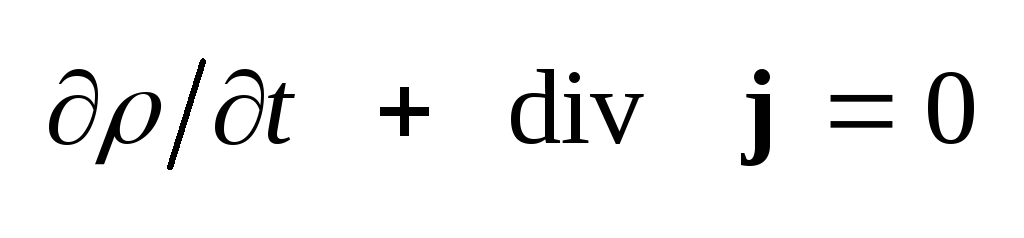 .
(1.21) и законом Ома ji
= ikEk,
(1.40) . В стационарном случае
при /t
= 0 получаем div
j
= 0, то есть (ijEj)/xi
= 0 (4.1) Уравнение (4.1) заменяет
для внутренних областей
проводника уравнение
(1.30), которое, в свою очередь,
позволяет найти
стационарное распределение
свободных зарядов по
найденному распределению
электрического поля.
Электрическое поле,
вызывающее ток в проводнике,
производит над перемещающимися
свободными зарядами
работу. Энергия поля
диссипирует в проводнике,
переходя в тепло. Процесс
диссипации энергии в
проводнике может быть
стационарным (но не
статическим) при наличии
в проводнике сторонних
сил fe
неэлектрического
происхождения, входящих
в правую часть уравнения
(1.5). Элементами проводящей
цепи, включающими
сторонние силы, могут быть
аккумуляторы .
(1.21) и законом Ома ji
= ikEk,
(1.40) . В стационарном случае
при /t
= 0 получаем div
j
= 0, то есть (ijEj)/xi
= 0 (4.1) Уравнение (4.1) заменяет
для внутренних областей
проводника уравнение
(1.30), которое, в свою очередь,
позволяет найти
стационарное распределение
свободных зарядов по
найденному распределению
электрического поля.
Электрическое поле,
вызывающее ток в проводнике,
производит над перемещающимися
свободными зарядами
работу. Энергия поля
диссипирует в проводнике,
переходя в тепло. Процесс
диссипации энергии в
проводнике может быть
стационарным (но не
статическим) при наличии
в проводнике сторонних
сил fe
неэлектрического
происхождения, входящих
в правую часть уравнения
(1.5). Элементами проводящей
цепи, включающими
сторонние силы, могут быть
аккумуляторы
|
11.2 .
(4.6) На поверхности проводников
должны выполняться
граничные условия (1.32)
Е1
= Е2.
и (1.35) D2n
– D1n
= 4.
. Из условия непрерывности
тангенциальной составляющей
электрического поля
с учетом того, что внутри
проводника Е
= 0, следует, что потенциал
постоянен на поверхности
Si
i-го
проводника: .
(4.6) На поверхности проводников
должны выполняться
граничные условия (1.32)
Е1
= Е2.
и (1.35) D2n
– D1n
= 4.
. Из условия непрерывности
тангенциальной составляющей
электрического поля
с учетом того, что внутри
проводника Е
= 0, следует, что потенциал
постоянен на поверхности
Si
i-го
проводника:
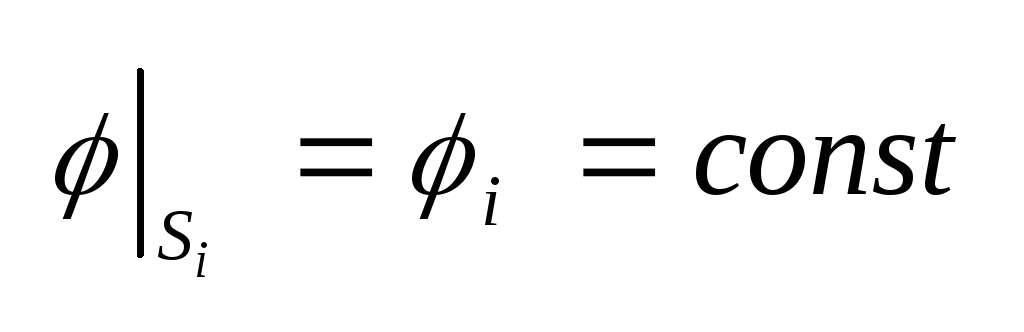 .
(4.7) Аналогично из условия
(1.35), учитывая, что в вакууме
D
= E,
а в проводнике D
= E
= 0, получим: .
(4.7) Аналогично из условия
(1.35), учитывая, что в вакууме
D
= E,
а в проводнике D
= E
= 0, получим:
 .
(4.8) Полный заряд qi
i-го
проводника можно найти,
интегрируя по его поверхности
соотношение (4.8): .
(4.8) Полный заряд qi
i-го
проводника можно найти,
интегрируя по его поверхности
соотношение (4.8):
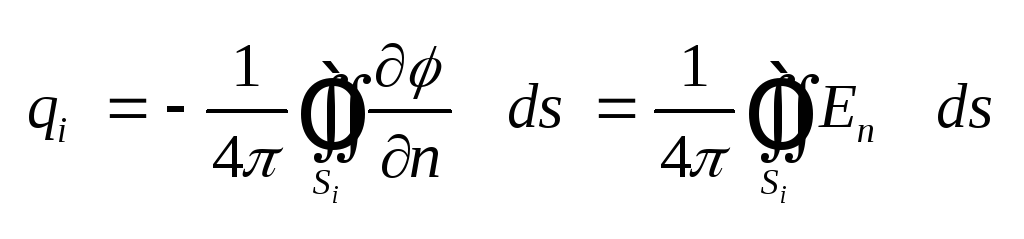 .
(4.9) Уравнение Лапласа
(4.5) с граничными условиями
(4.7) и нормировкой (4.6) (задача
Дирихле) имеет единственное
решение, а функции,
удовлетворяющие
уравнению Лапласа,
называются гармоническими.
В частности, задание
потенциалов всех проводников
i
однозначно определяет
распределение поверхностных
зарядов (4.8) на них и потенциала
(r)
в пространстве между
проводниками, который
меньше, чем наибольший из
потенциалов проводников
i,
и больше, чем наименьший. .
(4.9) Уравнение Лапласа
(4.5) с граничными условиями
(4.7) и нормировкой (4.6) (задача
Дирихле) имеет единственное
решение, а функции,
удовлетворяющие
уравнению Лапласа,
называются гармоническими.
В частности, задание
потенциалов всех проводников
i
однозначно определяет
распределение поверхностных
зарядов (4.8) на них и потенциала
(r)
в пространстве между
проводниками, который
меньше, чем наибольший из
потенциалов проводников
i,
и больше, чем наименьший.
|
11.3Аналогично,
подставляя E(r)
= –grad
(r),
получим
 .
Таким образом, .
Таким образом,
 .
(4.12) Соотношение (4.12)
называется теоремой
взаимности. Пусть в первом
случае отличен от нуля
потенциал только i-го
проводника, а во втором –
только j-го.
Тогда из формулы (4.10)
следует, что qj
= Cjii,
qi
= Cijj,
а теорема взаимности
(4.12) принимает вид iqi
= jqj,
откуда следует, что Cji
= Cij,
(4.13) то есть матрица (4.10)
симметричная. .
(4.12) Соотношение (4.12)
называется теоремой
взаимности. Пусть в первом
случае отличен от нуля
потенциал только i-го
проводника, а во втором –
только j-го.
Тогда из формулы (4.10)
следует, что qj
= Cjii,
qi
= Cijj,
а теорема взаимности
(4.12) принимает вид iqi
= jqj,
откуда следует, что Cji
= Cij,
(4.13) то есть матрица (4.10)
симметричная.
|
|
|
|
12.1Термодинамика
проводников Рассмотрим
энергию электростатического
поля, создаваемого
заряженными проводниками.
Как следует из формулы
 ,
(1.47) , плотность энергии
электростатического
поля равна w
= ED/(8).
Так как внутри проводников
Е
= 0, а вне их D
= E,
то для полной энергии поля
по аналогии с выводом
соотношения (4.12) с учетом
формул div
E
= 0. (4.3), E(r)
= – grad
(r).
(4.4) ,
(1.47) , плотность энергии
электростатического
поля равна w
= ED/(8).
Так как внутри проводников
Е
= 0, а вне их D
= E,
то для полной энергии поля
по аналогии с выводом
соотношения (4.12) с учетом
формул div
E
= 0. (4.3), E(r)
= – grad
(r).
(4.4)
 .
(4.6) , .
(4.6) ,
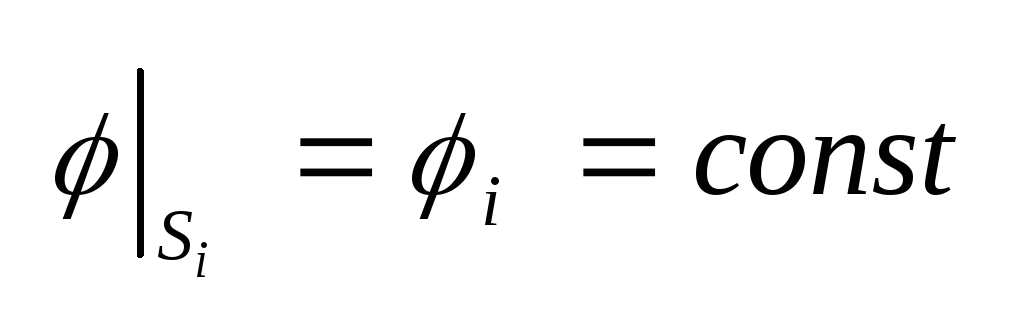 .
(4.7) и .
(4.7) и
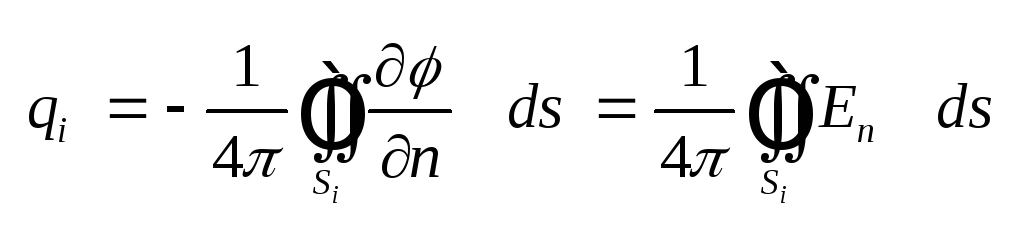 .
(4.9) получаем .
(4.9) получаем
 .
(4.14) Здесь интеграл по объему
берется по области
пространства вне
проводников. С учетом
формулы (4.11) соотношение
(4.14) можно записать в виде
квадратичной формы: .
(4.14) Здесь интеграл по объему
берется по области
пространства вне
проводников. С учетом
формулы (4.11) соотношение
(4.14) можно записать в виде
квадратичной формы:
 .
(4.15) Из условия существенной
положительности
квадратичной формы
(4.15) следует ряд неравенств,
которым должны удовлетворять
элементы матрицы Cij. .
(4.15) Из условия существенной
положительности
квадратичной формы
(4.15) следует ряд неравенств,
которым должны удовлетворять
элементы матрицы Cij.
|
12.2 .
(4.18) На заряженный проводник
в электрическом поле
действует сила, по общему
правилу равная производной
потенциальной энергии
системы по координатам
проводника, взятой с
обратным знаком. Формально
можно найти эту силу
дифференцированием
соотношений (4.16) или (4.18).
Так, для системы изолированных
проводников с фиксированными
зарядами .
(4.18) На заряженный проводник
в электрическом поле
действует сила, по общему
правилу равная производной
потенциальной энергии
системы по координатам
проводника, взятой с
обратным знаком. Формально
можно найти эту силу
дифференцированием
соотношений (4.16) или (4.18).
Так, для системы изолированных
проводников с фиксированными
зарядами
 .
(4.19) Однако на практике
удобнее выражать давление,
то есть силу, действующую
на единицу поверхности
проводника, через
напряженность поля вблизи
этой поверхности. Если
малый участок площадью s
переместится на малое
расстояние dr,
то при неизменном полном
заряде проводника
останется постоянным
плотность поверхностного
заряда
и, в силу формулы (4.8), поле
Е
на поверхности проводника.
Изменение энергии поля
составит dW
= –wsndr
= –E2sndr/(8),
где n
–внешняя нормаль к поверхности
проводника. Поскольку
на поверхности проводника
E
= nE,
для силы f,
действующей на единицу
поверхности проводника,
с учетом формулы (4.8) получаем
f
= EE/(8)
= E/2.
(4.20 .
(4.19) Однако на практике
удобнее выражать давление,
то есть силу, действующую
на единицу поверхности
проводника, через
напряженность поля вблизи
этой поверхности. Если
малый участок площадью s
переместится на малое
расстояние dr,
то при неизменном полном
заряде проводника
останется постоянным
плотность поверхностного
заряда
и, в силу формулы (4.8), поле
Е
на поверхности проводника.
Изменение энергии поля
составит dW
= –wsndr
= –E2sndr/(8),
где n
–внешняя нормаль к поверхности
проводника. Поскольку
на поверхности проводника
E
= nE,
для силы f,
действующей на единицу
поверхности проводника,
с учетом формулы (4.8) получаем
f
= EE/(8)
= E/2.
(4.20
|
|
|
|
|
|
|
|
получим
 .
(4.29) Для элемента однородной
среды, помещенной в
постоянное электрическое
поле, с учетом формулы
(4.29) получаем: .
(4.29) Для элемента однородной
среды, помещенной в
постоянное электрическое
поле, с учетом формулы
(4.29) получаем:
 ,
откуда следует, что ,
откуда следует, что
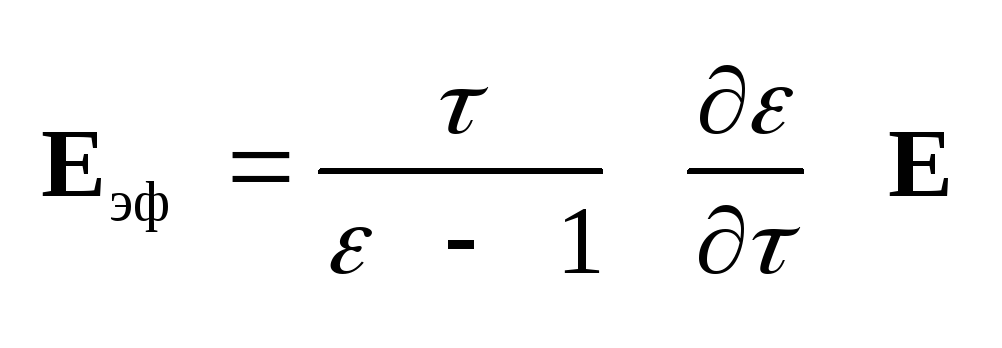 .
(4.30) Из формулы (4.30) следует,
что если диэлектрическая
проницаемость линейно
зависит от плотности, что
характерно для газов,
плазмы и других разреженных
сред, то есть
= 1 + с,
то эффективное поле
совпадает со средним полем
в среде. В конденсированных
средах диэлектрическая
проницаемость является
нелинейной функцией
плотности и эффективное
поле отлично от среднего.
Соотношение (4.30) позволяет
установить связь между
макроскопической
величиной – диэлектрической
проницаемостью – и
микроскопической
атомной поляризуемостью.
Поскольку р
= аЕэф,
то Р
= (
– 1)/(4)Е
= np
= nаЕэф.
Тогда .
(4.30) Из формулы (4.30) следует,
что если диэлектрическая
проницаемость линейно
зависит от плотности, что
характерно для газов,
плазмы и других разреженных
сред, то есть
= 1 + с,
то эффективное поле
совпадает со средним полем
в среде. В конденсированных
средах диэлектрическая
проницаемость является
нелинейной функцией
плотности и эффективное
поле отлично от среднего.
Соотношение (4.30) позволяет
установить связь между
макроскопической
величиной – диэлектрической
проницаемостью – и
микроскопической
атомной поляризуемостью.
Поскольку р
= аЕэф,
то Р
= (
– 1)/(4)Е
= np
= nаЕэф.
Тогда
 .
(4.31) n
= b,
получим: .
(4.31) n
= b,
получим:
 .
(4.32 .
(4.32
|
 .
(1.15) как среднего дипольного
момента среды необходимо
найти смещение связанных
зарядов под действием
электрического поля
в среде. При этом необходимо
учитывать, что сила,
действующая на принадлежащий
среде связанный заряд,
определяется не средним
полем, которое складывается
из поля внешних источников
и самосогласованного
поля, создаваемого
всеми зарядами среды,
включая рассматриваемый.
Сила же, действующая на
рассматриваемый
заряд, определяется
полем, созданным всеми
зарядами среды, кроме
рассматриваемого.
Хотя число всех остальных
зарядов в среде может быть
очень велико, вклад выделенного
заряда в суммарное поле
в ближайшей окрестности
этого заряда может быть
достаточно велик.
Поле, действующее на
отдельную частицу среды
или на отдельный поляризующийся
элемент среды, называется
эффективным полем.
Эффективное электрическое
поле не меньше среднего.
Рассмотрим эффективное
поле в среде на примере
жидкого однородного
изотропного диэлектрика.
В случае твердого диэлектрика
природа эффективного
поля не меняется, но
описание его усложняется,
поскольку силы, действующие
на элемент среды, приводят
не только к изменению
плотности, как в жидкости,
но и к сдвиговым напряжениям.
Пусть электрическое
поле в жидкости создается
неподвижными сторонними
зарядами и остается
постоянным при изменении
плотности жидкости. Тогда
изменение энергии
стационарного
электрического поля
в среде под действием сил
эффективного поля
связано только с изменением
диэлектрической
проницаемости среды.
Из формулы .
(1.15) как среднего дипольного
момента среды необходимо
найти смещение связанных
зарядов под действием
электрического поля
в среде. При этом необходимо
учитывать, что сила,
действующая на принадлежащий
среде связанный заряд,
определяется не средним
полем, которое складывается
из поля внешних источников
и самосогласованного
поля, создаваемого
всеми зарядами среды,
включая рассматриваемый.
Сила же, действующая на
рассматриваемый
заряд, определяется
полем, созданным всеми
зарядами среды, кроме
рассматриваемого.
Хотя число всех остальных
зарядов в среде может быть
очень велико, вклад выделенного
заряда в суммарное поле
в ближайшей окрестности
этого заряда может быть
достаточно велик.
Поле, действующее на
отдельную частицу среды
или на отдельный поляризующийся
элемент среды, называется
эффективным полем.
Эффективное электрическое
поле не меньше среднего.
Рассмотрим эффективное
поле в среде на примере
жидкого однородного
изотропного диэлектрика.
В случае твердого диэлектрика
природа эффективного
поля не меняется, но
описание его усложняется,
поскольку силы, действующие
на элемент среды, приводят
не только к изменению
плотности, как в жидкости,
но и к сдвиговым напряжениям.
Пусть электрическое
поле в жидкости создается
неподвижными сторонними
зарядами и остается
постоянным при изменении
плотности жидкости. Тогда
изменение энергии
стационарного
электрического поля
в среде под действием сил
эффективного поля
связано только с изменением
диэлектрической
проницаемости среды.
Из формулы
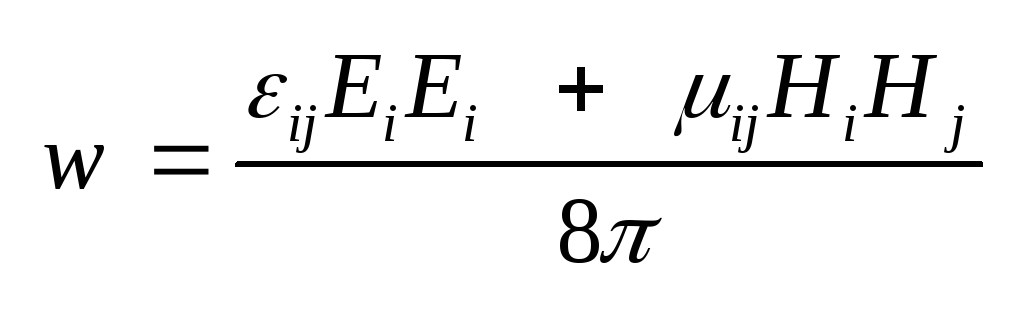 , ,
|
|
|
|
– (4.41)
среднее значение квадрата
дипольного момента
сферы за счет тепловых
флуктуаций. Поскольку
D
= E
= E
+ 4P,
а
 ,
то из формулы (4.40) следует: ,
то из формулы (4.40) следует:
 .
Этой формуле удобно придать
другой вид .
Этой формуле удобно придать
другой вид
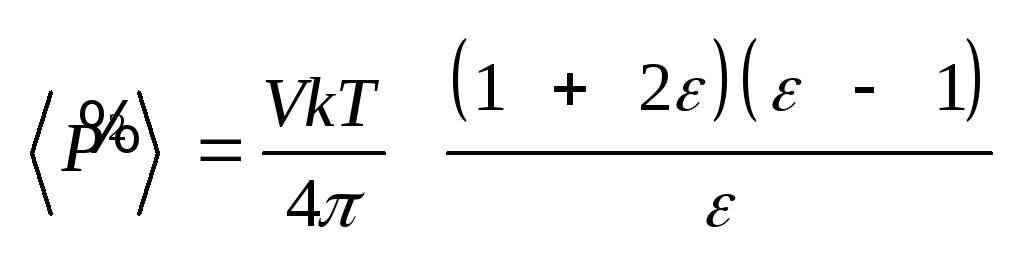 ,
(4.42) связывающий средний
квадрат спонтанного
(флуктуационного)
дипольного момента
сферической области
в отсутствии электрического
поля с диэлектрической
проницаемостью среды.
Такая связь является
частным случаем
флуктуационно-диссипативной
теоремы. Выразим входящий
в формулу (4.42) средний квадрат
дипольного момента
области как сумму дипольных
моментов составляющих
эту область частиц (атомов,
молекул, элементарных
ячеек и т. д.). Считая частицы
одинаковыми, а их плотность
равной n,
с учетом формулы (4.41) получаем: ,
(4.42) связывающий средний
квадрат спонтанного
(флуктуационного)
дипольного момента
сферической области
в отсутствии электрического
поля с диэлектрической
проницаемостью среды.
Такая связь является
частным случаем
флуктуационно-диссипативной
теоремы. Выразим входящий
в формулу (4.42) средний квадрат
дипольного момента
области как сумму дипольных
моментов составляющих
эту область частиц (атомов,
молекул, элементарных
ячеек и т. д.). Считая частицы
одинаковыми, а их плотность
равной n,
с учетом формулы (4.41) получаем:
 .
(4.43) Здесь (u)
– .
(4.43) Здесь (u)
–
|
Эта
энергия включает в себя
как взаимодействие
рассматриваемых
зарядов друг с другом, так и
их взаимодействие с
зарядами вне выделенной
сферы. Тогда потенциальная
энергия зарядов сферы в
однородном внешнем поле
Е
примет вид:
 ,
(4.37) где для суммарного
дипольного момента,
создаваемого зарядами
сферы, введено обозначение ,
(4.37) где для суммарного
дипольного момента,
создаваемого зарядами
сферы, введено обозначение
 .
Предполагается, что в
отсутствии внешнего
поля все направления
вектора .
Предполагается, что в
отсутствии внешнего
поля все направления
вектора
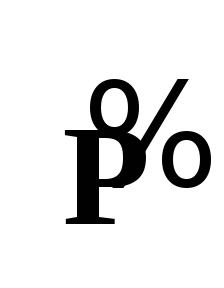 равноправны, поэтому
энергия U0
зависит только от модуля
вектора
равноправны, поэтому
энергия U0
зависит только от модуля
вектора
 .
Сферическая область
находится в тепловом
контакте с внешней частью
диэлектрика и через
нее – с термостатом. Плотность
вероятности того, что
сфера окажется в состоянии
с энергией .
Сферическая область
находится в тепловом
контакте с внешней частью
диэлектрика и через
нее – с термостатом. Плотность
вероятности того, что
сфера окажется в состоянии
с энергией
 дается распределением
Больцмана
дается распределением
Больцмана
 .
(4.38) Вычислим среднее
значение .
(4.38) Вычислим среднее
значение
|
водника
внутренней:
 .
Так как на поверхности
проводника в силу условия .
Так как на поверхности
проводника в силу условия
 .
(4.7) i
= const, выражение для работы
можно представить в виде
объемного интеграла: .
(4.7) i
= const, выражение для работы
можно представить в виде
объемного интеграла:
 .(4.33)
При выводе формулы (4.33)
использовано уравнение
E(r)
= – grad
(r).
(4.4) E(r)
= –grad
(r)
и тождество div
(
D)
=
div
D
+ D
grad
.
Интеграл в соотношении
(4.33) берется по всему объему
вне проводников, причем
интеграл по бесконечно
удаленной поверхности
равен нулю. Поскольку все
свободные и сторонние
заряды сосредоточены
на внешних проводниках,
вне их в силу условия (1.30) .(4.33)
При выводе формулы (4.33)
использовано уравнение
E(r)
= – grad
(r).
(4.4) E(r)
= –grad
(r)
и тождество div
(
D)
=
div
D
+ D
grad
.
Интеграл в соотношении
(4.33) берется по всему объему
вне проводников, причем
интеграл по бесконечно
удаленной поверхности
равен нулю. Поскольку все
свободные и сторонние
заряды сосредоточены
на внешних проводниках,
вне их в силу условия (1.30)
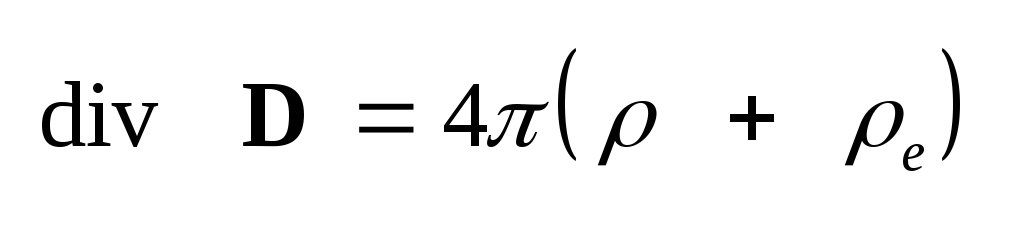 div
D
= 0. Внутри проводников
электрическое поле
и индукция равны нулю,
поэтому интегрирование
можно распространить
на все пространство.
Работа, произведенная
над изолированной системой,
равна изменению ее энергии.
Если при поляризации
диэлектрика его плотность
не меняется, для плотности
F
свободной энергии из формулы
(4.33) получаем dF
= –SdT
+ ED/(4),
(4.34) где S
– плотность энтропии. Для
равновесной системы,
когда индукция является
функцией состояния вида
(1.37), вариацию индукции
в
div
D
= 0. Внутри проводников
электрическое поле
и индукция равны нулю,
поэтому интегрирование
можно распространить
на все пространство.
Работа, произведенная
над изолированной системой,
равна изменению ее энергии.
Если при поляризации
диэлектрика его плотность
не меняется, для плотности
F
свободной энергии из формулы
(4.33) получаем dF
= –SdT
+ ED/(4),
(4.34) где S
– плотность энтропии. Для
равновесной системы,
когда индукция является
функцией состояния вида
(1.37), вариацию индукции
в
|
|
|
|
Величина
Тс
в формуле (4.60) называется
константой Кюри – Вейса,
для различных сегнетоэлектриков
порядок величины
постоянной Тс
составляет
103
... 105
К. Из закона Кюри – Вейса
(4.60) следует, что вблизи
температуры Кюри
диэлектрическая
проницаемость
параэлектрической
фазы резко возрастает.
В пироэлектрической
фазе, как следует из уравнения
(4.59), Е=
P
+ P3,
(4.61) причем поляризация
состоит из двух частей,
спонтанной поляризации
 и
индуцированной
поляризации Рин.
В слабых полях Рин
<< Рсп
и Рин
= –Е/2.
Таким образом, в
пироэлектрической
фазе диэлектрическая
проницаемость также
сильно возрастает вблизи
точки Кюри, причем и
индуцированной
поляризации Рин.
В слабых полях Рин
<< Рсп
и Рин
= –Е/2.
Таким образом, в
пироэлектрической
фазе диэлектрическая
проницаемость также
сильно возрастает вблизи
точки Кюри, причем
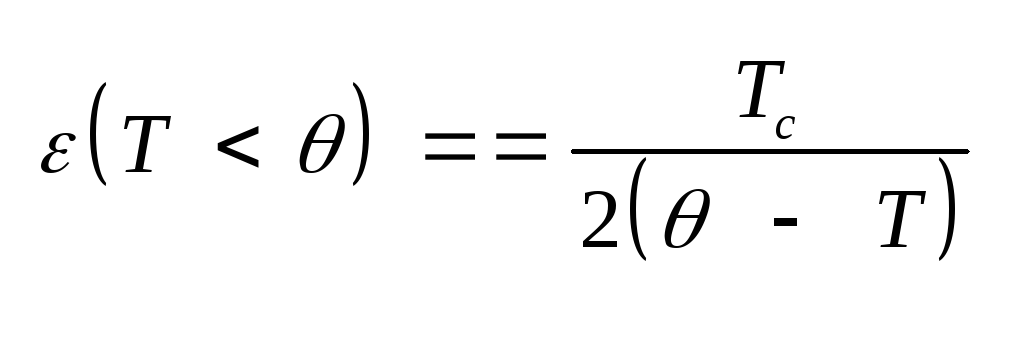 .
(4.62) Уравнение (4.61), если
разрешить его относительно
поляризации Р,
дает зависимость Р(Е)
поляризации от поля.
Нетрудно видеть, что при
< 0 эта зависимость
неоднозначна, причем
состоянию Р(0)
= 0 соответствует
отрицательная производная
dP/dE
=
< 0, то есть это состояние
неустойчиво. При плавном
увеличении напряженности
электрического поля
поляризация меняет
знак не одновременно с
изменением знака поля,
а только тогда, когда
поле достигнет определенной
величины Ec.
Это значение поля и определяет
коэрцитивную силу.
Соответственно, при
плавном уменьшении
напряженности
электрического поля
поляризация меняет
знак только при Е
= –Ес,
то есть появляется
диэлектрический
гистерезис. .
(4.62) Уравнение (4.61), если
разрешить его относительно
поляризации Р,
дает зависимость Р(Е)
поляризации от поля.
Нетрудно видеть, что при
< 0 эта зависимость
неоднозначна, причем
состоянию Р(0)
= 0 соответствует
отрицательная производная
dP/dE
=
< 0, то есть это состояние
неустойчиво. При плавном
увеличении напряженности
электрического поля
поляризация меняет
знак не одновременно с
изменением знака поля,
а только тогда, когда
поле достигнет определенной
величины Ec.
Это значение поля и определяет
коэрцитивную силу.
Соответственно, при
плавном уменьшении
напряженности
электрического поля
поляризация меняет
знак только при Е
= –Ес,
то есть появляется
диэлектрический
гистерезис.
|
Переход
сегнетоэлектрика
из параэлектрической
фазы, в которой спонтанной
поляризации нет, в
пироэлектрическую
фазу с неравной нулю
спонтанной поляризацией
может быть фазовым переходом
I или II рода. Независимо
от типа фазового перехода,
температура, при которой
происходит переход,
называется
сегнетоэлектрической
температурой Кюри .
Направление вектора
спонтанной поляризации
может быть изменено при
наложении внешнего поля
конечной величины,
называемой коэрцитивной
силой. При температуре
ниже температуры Кюри
в нулевом внешнем поле
сегнетоэлектрик
может разбиться на области
с противоположно
направленной поляризацией,
называемые доменами.
Это связано с тем, что в случае
однодоменного тела
конечных размеров вне
кристалла возникает
электрическое поле,
называемое деполяризующим.
При разбиении сегнетоэлектрика
на домены деполяризующее
поле сильно уменьшается.
Разбиение на домены
происходит так, что сумма
энергии деполяризующего
поля и поверхностной
энергии граничных слоев
минимальна. В сегнетоэлектриках
граница между доменами
имеет толщину порядка
нескольких межатомных
расстояний, у ферромагнетиков
толщина переходной
области намного больше.
Рассмотрим фазовый
переход второго рода
однодоменного
сегнетоэлектрика
вблизи температуры Кюри
без учета внутренних
напряжений. Поскольку
свободная энергия изотропного
тела не зависит от направления
вектора поляризации
Р,
она может быть записана в
виде ряда по четным степеням
спонтанной поляризации:
F
= F0
+ P2/2
+ P4/4
+ ...., (4.53) где F0
– плотность свободной энергии
в параэлектрической
фазе. Поляризация, при
которой свободная энергия
имеет экстремальное
значение, определяется
из условия равенства
нулю производной выражения
(4.53): P
+ P3
=
|
 .
Проинтегрируем это
уравнение, учитывая, что
р(Е
= 0) = р0: .
Проинтегрируем это
уравнение, учитывая, что
р(Е
= 0) = р0:
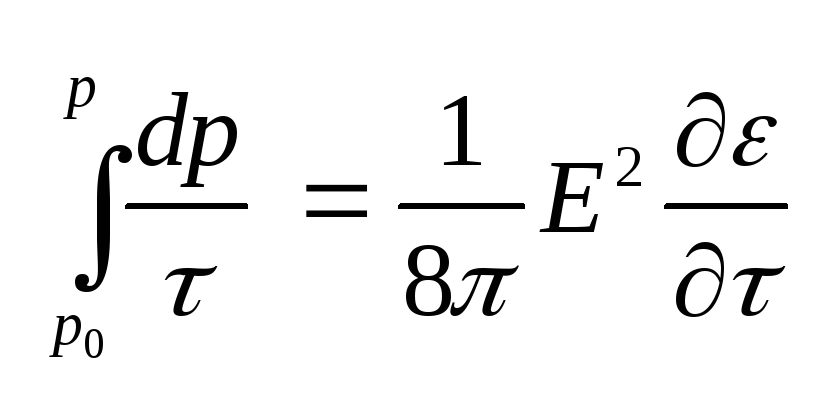 .
Для несжимаемых жидкостей
плотность не зависит от
давления, поэтому
в подынтегральном выражении
можно считать постоянным.
В этом случае электрострикционное
изменение давления,
обусловленное включением
электрического поля,
описывается формулой .
Для несжимаемых жидкостей
плотность не зависит от
давления, поэтому
в подынтегральном выражении
можно считать постоянным.
В этом случае электрострикционное
изменение давления,
обусловленное включением
электрического поля,
описывается формулой
 .
(4.47) Квадратичная
зависимость тензора
напряжений (4.46) и
электрострикционного
давления (4.47) в жидкостях
от электрического
поля связана с тем, что
изменение диэлектрической
проницаемости жидкости
обусловлено только
изменением ее плотности
в данной точке. В кристаллических
твердых телах деформация,
например сдвиговая, и
соответствующее
изменение диэлектрической
проницаемости могут
происходить и без изменения
плотности среды. В этом случае
внутренние напряжения
в среде могут оказаться
пропорциональными
полю. Среды, в которых
деформация линейно
зависит от приложенного
поля, называются
пьезоэлектриками.
Для пьезоэлектрика
вектор электрической
индукции зависит не только
от электрического
поля, но и от тензора
напряжений: Di
= ijEj
+ ijkjk. .
(4.47) Квадратичная
зависимость тензора
напряжений (4.46) и
электрострикционного
давления (4.47) в жидкостях
от электрического
поля связана с тем, что
изменение диэлектрической
проницаемости жидкости
обусловлено только
изменением ее плотности
в данной точке. В кристаллических
твердых телах деформация,
например сдвиговая, и
соответствующее
изменение диэлектрической
проницаемости могут
происходить и без изменения
плотности среды. В этом случае
внутренние напряжения
в среде могут оказаться
пропорциональными
полю. Среды, в которых
деформация линейно
зависит от приложенного
поля, называются
пьезоэлектриками.
Для пьезоэлектрика
вектор электрической
индукции зависит не только
от электрического
поля, но и от тензора
напряжений: Di
= ijEj
+ ijkjk.
|
|
|
|
|
Величину
термоэлектродвижущей
силы можно получить из
соотношения (4.63),
переписанного в виде
E
= (j
– grad
T)/.
(4.75) Положив для разомкнутой
цепи j
= 0 и проинтегрировав это
соотношение вдоль цепи,
получим:
 .
(4.76) Коэффициенты Пельтье
П и Томсона
не являются независимыми.
Сравнивая соотношения
(4.71), (4.73) и (4.74), получим
= Td(П/T)/dT.
(4.77) Тогда формулу (4.76)
можно переписать в виде .
(4.76) Коэффициенты Пельтье
П и Томсона
не являются независимыми.
Сравнивая соотношения
(4.71), (4.73) и (4.74), получим
= Td(П/T)/dT.
(4.77) Тогда формулу (4.76)
можно переписать в виде
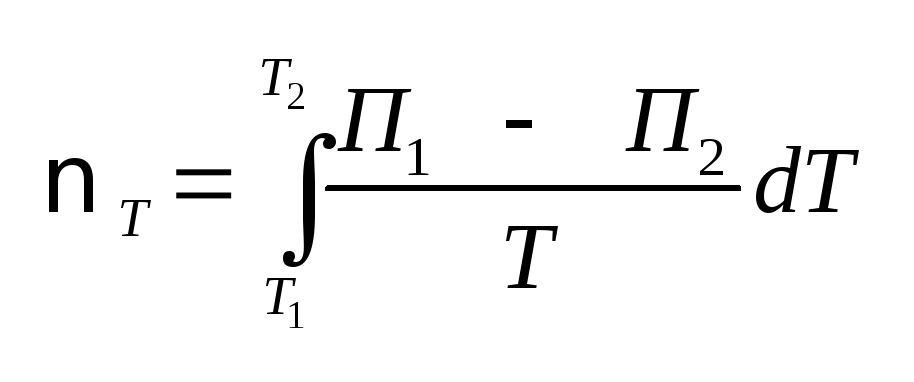 .
(4.78) Формулы (4.77) и (4.78) называются
соотношениями Томсона .
(4.78) Формулы (4.77) и (4.78) называются
соотношениями Томсона
|
Обозначим
через Ji
плотность потока какой-либо
физической величины,
тогда скорость изменения
плотности энтропии в среде
равна dS/dt
= –JiXi.
(4.65) Величины Xi
в соотношении (4.65)
называются обобщенными
силами, а сами потоки Ji
выражаются линейно
через обобщенные силы Ji
= ijXj
(4.66) Формулу (4.66) можно
рассматривать как
определение кинетических
коэффициентов.
Математическая
формулировка принципа
Онсагера, который
доказывается в курсе
статистической физики,
гласит ij
= ji.
(4.67) При наличии в среде
тепловыделения и
градиента температуры
закон сохранения энергии
принимает вид dS/dt
= (jE
– div
s)/T
= –[–jE/T
– s
grad
(1/T)]
– div
(s/T)
(4.68) Последнее слагаемое
в правой части формулы
(4.68) при интегрировании
по объему должно обратиться
в нуль, так как через внешнюю
поверхность тела поток
тепла отсутствует.
Тогда из выражений (4.65)
и (4.68) следует, что в среде
имеются две обобщенные
силы Xj
= –E/T
и Xs
= –grad
(1/T).
В свою очередь, из сравнения
уравнений (4.63), (4.64) и (4.66) следует,
что jj
= T,
js
= –T2,
sj
= T,
ss
= –T2.
(4.69) Из формул (4.69) и принципа
Онсагера (4.67) вытекает,
что
= –T.
(4.70) Выражение для плотности
потока тепла (4.64) с учетом
формул (4.63) и (4.70) может быть
записано в виде s
= –jT/
– grad
T,
(4.71) где обозначено
= –(
+ 2T/).
Тогда из формулы (4.68)
следует, что полная плотность
мощности, выделяющейся
в среде в виде тепла, равна
dQ/dt
= (j2/
– j
grad
T)/
+ div
s
= j2/
+ jTgrad(/)
+ div(grad
T).
(4.72) Первое слагаемое в
правой части формулы
(4.72) является джоулевым
тепловыделением,
третье – обусловлено
теплопроводностью.
Второе же слагаемое связано
с термоэлектрическими
эффектами. Его вклад в
тепловыделение
линеен по j,
поэтому он может быть как
положительным, так и
отрицательным, в зависимости
от направления тока.
|


 .(3.51)
.(3.51) (3.54) Подставляя формулы
(3.51), (3.52), (3.53) и (3.54) в левую часть
усредненного по периоду
уравнения (3.46) и учитывая,
что
(3.54) Подставляя формулы
(3.51), (3.52), (3.53) и (3.54) в левую часть
усредненного по периоду
уравнения (3.46) и учитывая,
что