Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Ярославский Государственный Медицинский Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

lim

.pdf

Скачиваний:

Добавлен:

24.03.2016

Размер:

276.82 Кб

Скачать

☆

<<< < Предыдущая 12 / 22

Следствие. Если функция f(x) имеет предел при x ! x0, тогда:

lim (f(x))n = ( lim f(x))n;

x!x0 x!x0

lim Cf(x) = C lim f(x);

x!x0

где n – натуральное число, а C – константа.

lim(5x2

Пример 11. Вычислить предел функции x 2

Пользуясь свойствами пределов получаем:

lim(5x2

1) = 5 lim x2

lim 1 = 5

1 = 19:

lim

2x2 1

Пример 12. Вычислить предел функции x!2

x3 + 2

lim(x3 + 2) = lim x3 + lim 2 = 8 + 2 = 10 = 0:

lim 1 = 8

1 = 7:

Далее воспользуемся свойствами пределов:

lim(2x2

1) = 2 lim x2

lim(2x2

lim

x!2

x3 + 2

lim(x3 + 2)

10:

Два выше приведенных примера показывают, что в случае непрерывной функции вычисление предела функции в точке сводится к подстановке предельного значения x в аналити-

ческое выражение, задающее функцию.
lim	x2 + 2x 8	.
Пример 13. Вычислить предел функции x!2	x3 8	.

Вданном примере пределы числителя и знаменателя равны 0. В этом случае говорят, что

имеется неопределенность

. Таким образом, свойства пределов применить нельзя. Раз-

ложим числитель и знаменатель на множители, получим: lim

(x 2)(x + 4)

: Разделим

(x 2)(x2 + 2x + 4)

x!2

lim

x + 4

числитель и знаменатель на

2, получим: x!2

x2 + 2x + 4

lim

x 4 + x

Пример 14. Вычислить предел функции x!0

Пределы числителя и знаменателя равны 0. Для того, чтобы вычислить этот предел, умножим и числитель и знаменатель на сопряженное к числителю выражение. Выражение, сопряженное к данному – это такое выражение, которое дополняет данное до какойли- бо формулы сокращенного умножения. В нашем примере до формулы разности квадратов.

Таким образом, получаем:

x!0

x(p4 x + p4 + x)

lim

4 + x

= lim

(

4 + x)(

x +

4 + x)

= lim

x!0 x(p4 x + p4 + x)

x!0 (p4 x + p4 + x)

lim

1 + 1

Пример 15.

Вычислить предел функции x!0

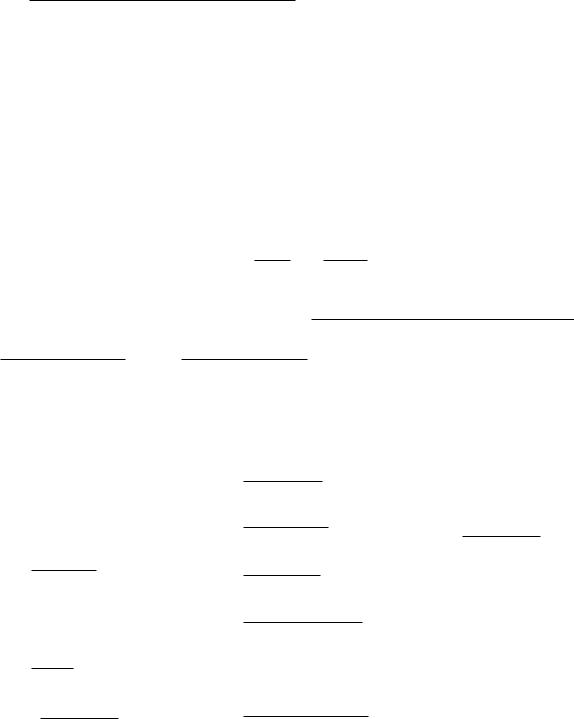
Умножим числитель и знаменатель на сопряженное выражение к числителю. То есть на

(p3

1)2

выражение

p3 x

1 + 1, которое дополняет числитель до формулы суммы кубов.

+ 1)((p

+ 1)

lim

1)2

x 1

= lim

x!0

x((p3 x

1)2

p3 x

1 + 1)

x!0

x((p3 x

1)2

p3 x

1 + 1)

lim

x!0 ((p3 x 1)2 p3 x 1 + 1)

При исследовании функций приходится рассматривать пределы, когда аргумент стремится к 1:

Определение 5. Пределом функции f(x) при стремлении x к 1 называется число A, если для любого числа " > 0 существует такое число (") > 0, что для всех x, для которых выполняется условие jxj > , выполняется неравенство jf(x) Aj < ". Записывают следующим образом: lim f(x) = A. Предел функции при x, стремящемся к 1, определяется

x!1

аналогично.

Техника нахождения пределов функций при x ! 1 аналогично вычислению пределов последовательностей.

Пример 16. Вычислить предел xlim (

x + 1

2x + 3).

lim (p

lim

( x + 1

2x + 3)

x + 1 +

2x + 3

x + 1

2x + 3)

x!1

(px + 1 + p2x + 3)

lim

(x + 1) (2x + 3)

= lim

x 2

x!1 px + 1 + p2x + 3 x!1 px + 1 + p2x + 3

3.2Задачи для самостоятельного решения

Вычислить пределы функций.

lim(x2 + 2x

1):

4x + 3

15.

lim

x2 + x

x!1

2x + 1

lim

6x2 + 5

2x 6

lim

4x + 3 .

+ x

16.

lim

4x3 3x2

x!1 x

+ 4x + 5

lim

10.

lim

x + 3

x!0

+ 5

+ x

+ 6

x 1

x!1

17.

lim

x + 1

lim

x!1

x2 + 3

lim

11.

1 + x

1 x

x!0

18.

x4 + x5

lim

1 +

lim

12.

lim

x!1 x

+ x

x!3

x 3

x! 1 1 + x

lim (p

19.

1 + x

1).

1 + x

lim

+ 4x 5

13.

lim

1 + x

x!1

x + 5

1 + x

lim (p

20.

x2 + 3x

+ 27

x!1

lim

14.

lim

2x + 4).

x! 3 x + 3

x!0

p1 + x p1

3.3Задачи домашней работы

Вычислите пределы функций.
	x3 + 1		2. lim	p		+ 1	.		x2 + x	.
1. lim		.			x			3. lim
x!3 x 1			x!1 x 1					x!0	x2 + 3x

+ x 6

lim

1 + x + x2

10.

1 x

1 + x

x!2

x 0

11.

2 + x

3x 2

lim

xlim

2x2 x + 1

1 + x2

lim

x!1 x 1 .

x!2

p4x + 1 p5x 1

12.

lim

px3 + 2x2

x + 1

5x + 6

9 + 2x

lim

3!1

2 3

x!3 x2

x!8

6x + 9

px 2

1 + x + x .

4Практическое занятие №4. Первый и второй замечательный пределы

4.1Первый и второй замечательный пределы

Теорема 4 (Первый замечательный предел). lim

sin x

= 1.

x!0

lim

1 +

= e

Теорема 5

(Второй замечательный предел). x!1

Пример 17. Вычислить предел lim(1 + x)x .

x!0

Сделаем замену переменной t =

! 1, тогда предел принимает вид:

t!1

lim

1 +

= e

Пример 18. Вычислить предел lim sin 2x.

x!0 x

Используем первый замечательный предел

lim	sin 2x	= lim	sin 2x	2 = 1	2 = 2:
	x		2x
x!0		x!0

lim

sin 2x

! 0 при

! 0.

x!0

= 1, так как 2

x + 3

lim

Пример 19. Вычислить предел x!1

Воспользуемся вторым замечательным пределом

x!1

x 2

= x!1

x!1

x + 3

3 x

lim

1 +

= lim

1 +

= lim

1 +

e3 :

Пример 20. Вычислить предел lim

ln(1 + x)

x!0

lim

ln(1 + x) = lim ln(1 + x)x = 1.

x!0

4.2Задачи для самостоятельного решения

lim

sin x

lim

tgx

sin x

x 0

x!0

x 0

lim

sin 2x

lim

cos x

lim

sin 2x

x!0

sin 4x

lim

10.

sin2 4x

lim

x!0 tg5x

x!0

sin 7x

11.

x!1

2x + 3

tg2x

2x 1

lim

x!1

3x + 6

x!0

2x2

3x + 7

lim

sin

12.

lim

4.3Задачи домашней работы

1. lim 3 sin 4x,

x!0 2x

2. lim x , x!0 sin x

cos x

3. lim p ,

x!0 x

4. lim tg x,

x!0 x

5. lim sin2 2x, x!0 sin2 4x


6.	lim	2x		,
6.	lim			,
	x!0	tg3x
			p
	lim	sin 2x
7.						,
		tgp2x
	x!0	tgp2x
8.	lim	sin2 2x			,
8.	lim				,
	x!0	3x3
9.			4x + 3				x
9.	x!1 4x 3						,
	lim

13. lim(3x 2)x ,

x!1

14. lim(1 + tgx)2x ,

x!0

15.	lim	ln(1 sin x)							.
	x!0			2x
10.	x!1		2x + 6					x
10.	x!1		2x + 1					,
	lim
11.	lim					2	,
	lim(4x				3)	2
	lim(4x				3)	3x
	x 1
	!

12. lim(1 + tg3x)x ,

x!0

13. lim ln(1 tgx).

x!0 2x

5Практическое занятие №5. Непрерывность функции. Асимптоты функции

5.1Непрерывность функции

Определение 6. Функция f(x) называется непрерывной в точке x0, если lim f(x) = f(x0).

x!x0

Функция f(x) называется непрерывной на данном множестве, если она непрерывна в каждой точке этого множества. Точки, в которых функция не является непрерывной, называются точками разрыва. Различают: 1) точки разрыва первого рода, для которых существуют ко-

нечные односторонние пределы		lim	f(x) и lim f(x), и точки разрыва второго рода - все
	x!x0 0		x!x0+0
остальные. Разность lim f(x)-		lim	f(x) называется скачком функции в точке x0. Если
	x!x0+0	x!x0 0
lim	f(x)= lim f(x), то точка x0 называется точкой устранимого разрыва.
x!x0 0	x!x0+0

Теорема 6. Основные элементарные функции непрерывны в тех точках, где они определены.

Теорема 7. Если функции f(x) и g(x) непрерывны в точке x0, то непрерывны в этой точке и функции f(x) g(x), f(x)g(x), fg((xx)) (g(x0) 6= 0).

Теорема 8. Если функция y = f(x) непрерывна в точке x0, а функция z = g(y) непрерывна в точке y0 = f(x0), то функция z = g(f(x)) непрерывна в точке x0:

Пример 21. Функции f(x) = ex и g(x) = sin x непрерывны в точке x0 = 1: Тогда функция h(x) = ex sin x будет непрерывна в точке x0 = 1: Сложная функция z = sin(ex) будет непрерывна в точке x0 = 1.

Теорема 9. Всякая элементарная функция непрерывна во всех точках из ее области определения.

5.2Асимптоты функции

Определение 7. Пусть	lim f(x) =	1. Тогда прямая	x = a	называется вертикальной
Определение 7. Пусть	x a	1. Тогда прямая		называется вертикальной
	!

асимптотой графика функции y = f(x).

Определение 8. Прямая, задаваемая уравнением y = kx+b, называется наклонной асимп-

тотой, если lim (f(x) kx b) = 0.

x!1

Из определения непосредственно следует, что k = f(x), а b = lim (f(x) kx).

x x!1

5.3Задачи для самостоятельного решения

Исследовать на непрерывность функции.
1.	f(x) =		2				,		3.	f(x) = sin					1	,				5.	f(x) =			1		,
1.	f(x) =						,		3.	f(x) = sin						,				5.	f(x) =					,
			x 1											x									sin x
2.	f(x) =		sin x			,				f(x) =				x2 1
									4.										,	6.	f(x) = psin x.
			jxj
													x2 3x + 2
													x2 3x + 2
Найти асимптоты графика функции.
		3x									2x 1									7.	y = p						,
1.	y =	3x			,				4.	y =	2x 1						,						x2 + 1
1.	y =				,				4.	y =							,						x2 + 1
		2x + 1									(1 x)2
2.	y =	2		,					5.		9 + 6x 3x2							,		8.	y =	ln x			,
2.	y =			,					5.	y =	9 + 6x 3x2							,		8.	y =				,
		1 x									x2			2x + 13								x
3.	y =		4					,	6.	y = p3							,			9.	y = xe x.
												x3 2
		3 + 2x x2										x3 2

5.4Задачи домашней работы

Исследовать на непрерывность функции.
1.	f(x) =				4			,	4.	f(x) =					x2 4						,	7.	f(x) =			1		,
1.	f(x) =							,	4.	f(x) =					x2 4						,	7.	f(x) =					,
		x2 2x 3												x2 4x + 3											tgx
2.	f(x) =		j sin xj			,			5.	f(x) =			1						,			8.	f(x) = logx2 4x+3 2,
		jx 1j
3.		jx 1j												cos x
3.	f(x) = cos				x ,				6.	f(x) = psin x,												9.	f(x) = ptgx.
					1
Найти асимптоты графика функции.
		2x + 5							4.					x				,				7.	y = p						,
1.	y =				,					y =				x											3x2 + 2
													x)			2
		2x 2														2
		2x 2								(1														ln x
2.	y =	1		,					5.	y =	9 + 6x x2									,		8.	y =	ln x			,
2.	y =			,					5.	y =	9 + 6x x2									,		8.	y =				,
		2 + x									x2 2x + 2													x + 2
3.	y =	1					,		6.	y = p1							,					9.	y = (x + 1)e x.
												x3 8
		4 + 3x x2										x3 8

6Примерная контрольная работа

Вариант 1

1. Докажите, что lim 2n4 5n = 2.

n!1 n4

2. Вычислите предел lim x4 + 2x2 3. x!1 x2 3x + 2

3.	Вычислите предел xlim (		x2 + 2 x2 + 4x + 5).
	!1
	Вычислите предел lim	p3		1	.
4.			1 + x + x2

	x!0		x(x2 + 2)

lim

5 n6

+ 2n4 1 + 3 n2 n 2

Вычислите предел n

+ 2n n + 1 +

Вычислите предел lim

sin3x + sin22x

x!0

(2x)2

n+1

lim

Вычислите предел x!1

Вычислите предел lim

ln(2x 1)

x!1 x2 3x + 2

Напишите уравнения

вертикальных

и наклонных асимптот функции

f(x) =

3x2 2x + 3

x + 1

10.

Исследовать на непрерывность функцию f(x) =

x2 3x + 2

x2 5x + 6

Вариант 2

1. Докажите, что lim 3n3 2n = 3.

n!1 n3

2. Вычислите предел lim x4 + 3x2 4. x!1 x2 4x + 3

3. Вычислите предел lim ( x2 + 5x 2 x2 + 3x 4).

x!1

lim

5x(x3 + 8)

Вычислите предел x!0

1 + x

1 x

lim

6 n5 + 2n4 1 + 3 n2 n 2

Вычислите предел n!1

n4 + 2n3 n + 1

+ p3 n2 .

Вычислите предел lim

sin3x + sin22x

x!0

(3x)2

4n + 1

2n 5

lim

4n 3

Вычислите предел x!1

Вычислите предел lim

ln(2x 3)

x!2

x2 3x + 2

Напишите уравнения

вертикальных и наклонных асимптот функции

f(x) =

2x2 2x + 1

3x 1

x2 2x + 2

10.

Исследовать на непрерывность функцию f(x) =

x2 6x + 7

7Список литературы

1.И.И.Баврин Курс высшей математики. Москва. Владос, 2004.

2.Б.П.Демидович Сборник задач и упражнений по математическому анализу. Издательство Московского университета, 1997.

<<< < Предыдущая 12 / 22

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.04.2015139.78 Кб925Lektsii_1-4_informatika.doc
#
21.04.2015173.57 Кб203lektsii_uef[1].doc
#
14.03.2015713.22 Кб84Lektsii_Uglova_propedevtika.doc
#
21.04.201533.72 Кб64lera (1).docx
#
14.03.2015318.68 Кб1654lim.pdf
#
24.03.2016276.82 Кб73lim.pdf
#
21.11.2019178.69 Кб11Lipidy.doc
#
24.03.2016267.47 Кб1670Lyubimaya_farma.docx
#
24.03.201640.68 Кб89manipulyatsii_stazhirovka.docx
#
14.03.201576.29 Кб16marshrutnaya_knijka.doc
#
24.03.2016914.43 Кб24Matematika_Zadachnik.doc