
lim
.pdfМатематический анализ. II семестр. Предел функции
М.А.Заводчиков 13 января 2015 г.
Содержание
1 |
Практическое занятие №1. Понятие функции |
3 |
|
|
1.1 |
Обзор основных элементарных функций . . . . . . . . . . . . . . . . . . . . . . |
3 |
|
1.2 |
Операции над функциями . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
5 |
|
1.3 |
Задачи для самостоятельного решения . . . . . . . . . . . . . . . . . . . . . . . |
6 |
|
1.4 |
Задачи домашней работы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
6 |
2 |
Практическое занятие №2. Предел последовательности. |
7 |
|
|
2.1 |
Предел числовой последовательности . . . . . . . . . . . . . . . . . . . . . . . . |
7 |
|
2.2 |
Задачи для самостоятельного решения . . . . . . . . . . . . . . . . . . . . . . . |
9 |
2.3Задачи домашней работы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
3 Практическое занятие № 3. Предел функции. |
10 |
3.1Предел функции . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
3.2Задачи для самостоятельного решения . . . . . . . . . . . . . . . . . . . . . . . 12
3.3Задачи домашней работы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
4 Практическое занятие №4. Первый и второй замечательный пределы |
13 |
4.1Первый и второй замечательный пределы . . . . . . . . . . . . . . . . . . . . . 13
4.2Задачи для самостоятельного решения . . . . . . . . . . . . . . . . . . . . . . . 13
4.3Задачи домашней работы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
5Практическое занятие №5. Непрерывность функции. Асимптоты функции 14
5.1 Непрерывность функции . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
5.2 Асимптоты функции . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
5.3Задачи для самостоятельного решения . . . . . . . . . . . . . . . . . . . . . . . 15
5.4Задачи домашней работы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
6 |
Примерная контрольная работа |
15 |
7 |
Список литературы |
18 |
Введение
Одной из тем, изучаемых в курсе "Математического анализа"специальности "Биохимия является "Предел функции". Понятие предела функции применяется для исследования функций (понятие непрерывности, нахождение асимптот), а также служит фундаментом для введения таких понятий как производная функции и определенный интеграл.
Целью настоящего методического пособия является поддержка практических занятий по теме "Предел функции". Работа содержит краткую теоретическую справку, большое количество подробно разобранных примеров, задачи для самостоятельной работы, задачи домашней работы, а также несколько вариантов контрольной работы. Рассматриваются не только элементарные функции, изучаемые в школе, но и функции обычно не встречающиеся в школьном курсе математики. По мнению автора это добавляет элемент исследования.
1Практическое занятие №1. Понятие функции
В настоящем парагарафе мы напоминаем, известное из школьного курса математики, определение функции. Далее идет краткий обзор элементарных функций, вводятся операции сложения функций, умножения на число функции, умножения функций, а также частное двух функций. Обсуждается понятие композиции функций. В задачах для самостоятельной работы рассматриваются некоторые функции, обычно не встречающиеся в школьном курсе математики, например: y = [x], y = fxg, y = xx, y = logx a и другие.
1.1Обзор основных элементарных функций
1.Целая рациональная функция – это функция вида:
f(x) = anxn + an 1xn 1 + ::: + a1x + a0; :
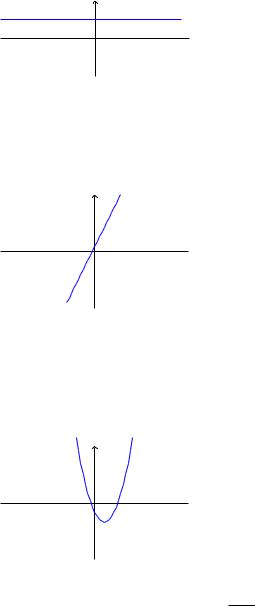
где an, an 1,...,a0 – некоторые действительные числа, а n – натуральное число. Простейшим примером целой рациональной функции является постоянная функция f(x) = b. Ее график выглядит вот так:
y
y = b  x
x
Область определения D(f) постоянной функции будет множество действительных чисел R. Область значений E(f) постоянной функции есть число b.
Следующим примером целой рациональной функции является линейная функция f(x) = kx + b. Ее график - прямая.
y
y = kx + b
 x
x
Область определения D(f) линейной функции будет множество действительных чисел R. Область значений E(f) постоянной функции есть множество действительных чисел
R.
Примером целой рациональной функции является квадратичная функция f(x) = a2x2 + a1x + a0. График этой функции парабола.
yy = a2x2 + a1x + a0
 x
x
Область определения D(f) квадратичной функции - множество действительных чисел
R. E(f) = [f(x0); 1), где x0 = a1 2a2
случае a2 < 0 получаем E(f) = ( 1; f(x0)).
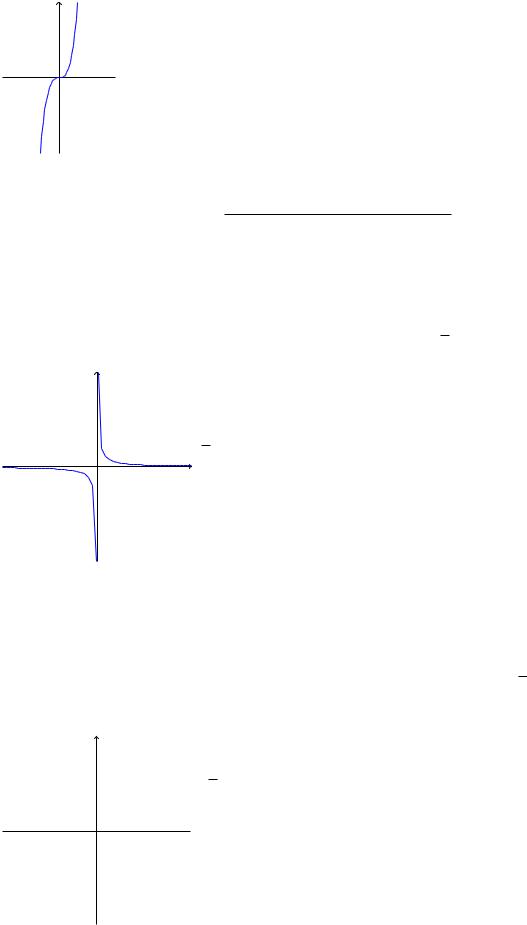
Функция f(x) = x3 также является примером целой рациональной функции с областью определения D(f) = ( 1; +1) и областью значений E(f) = ( 1; +1).
y
y = x3
 x
x
2. Дробно-рациональная функция – функция вида:
f(x) = anxn + an 1xn 1 + ::: + a1x + a0 ; bmxm + bm 1xm 1 + ::: + b1x + b0
где an, an 1,...,a0, bm,...,b0 – некоторые действительные числа, а n и m – натуральные числа.
Область определения D(f) дробно-рациональной функции – все действительные числа кроме тех, в которых обнуляется знаменатель. Примером дробно-
рациональной функции может служить функция f(x) = x1 . Ее график гипербола.
y |
|
y = |
1 |
|
x |
|
x |
Область определения D(f) = ( 1; 0) [ (0; 1). Область значений E(f) = ( 1; 0) [
(0; 1).
3. Степенная функция – это функция вида: f(x) = x ; где действительное число. Она определена при всех значениях x, если – натуральное число; при всех x кроме 0,
если – целое отрицательное число, и при x > 0, если – произвольное действительное p
число. Примером степенной функции может служить функция f(x) = x. График этой функции имеет вид:
y
p y = x
 x
x
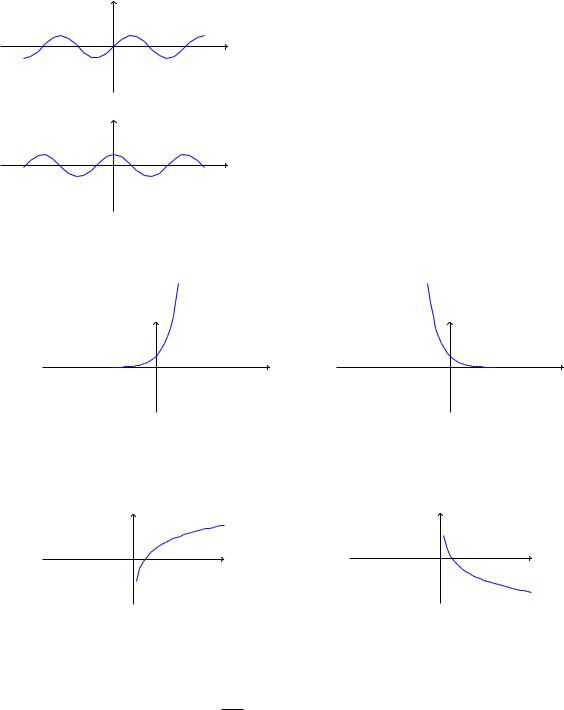
4. Тригонометрические функции. К тригонометрическим функциям относятся следующие y = sin x, y = cos x, y = tgx, y = ctgx и обратные к ним. Для функций y = sin x и cos x область определения D(y) = (1; +1). Область значений для этих функций есть E(y) = [ 1; 1]. Функция y = tgx не определена в точках x = 2 + n, где n 2 Z. Область значений E(y) = (1; +1). Функция y = ctgx не определена в точках x = n, где n 2 Z. Область значений E(y) = (1; +1). Ниже представлены графики тригонометрических функций.
y |
y =xsin x |
y |
y= cos xx
5.Показательная функция. Показательная функция - это функция вида y = ax, где a > 0. Область определения D(y) = (1; +1), а E(y) = (0; +1).
y = ax |
|
y |
y |
x |
y = ax |
x |
|
a > 1 |
a < 1 |
6.Логарифмическая функция. Логарифмическая функция - это функция, задаваемая
так: y = loga x, где a - положительное число, отличное от 1. D(y) = (0; +1), E(y) = (1; +1).
y |
|
y |
y = log2 x |
|
|
x |
|
x |
a > 1 |
a < 1 |
y = log0:5 x |
|
1.2Операции над функциями
Операции сложения функций, умножения функции на число, умножения функций, а также частное двух функций определяются поточечно, то есть (f + g)(x) = f(x) + g(x), ( f)(x) =f(x), (fg)(x) = f(x)g(x), fg (x) = fg((xx)) . Композиция двух функций определяется так: (f g)(x) = f(g(x)).
Пример 1. Даны функции f(x) = sin x и g(x) = x2. Выписать следующие функции: f g,
g f, f f, g g f.
f g = sin(x2), g f = sin2 x, f f = sin(sin x), g g f = sin4(x).

Определение 1. Функции, которые получаются из основных элементарных функций с помощью операций сложения, умножения на число, умножения функций, деления функций и композиции функций, называются элементарными функциями.
Элементарные функции достаточно подробно изучаются в школьном курсе математики. Приведем примеры функций, обычно не изучаемых в школе, f(x) = [x] - целая часть числа x, f(x) = fxg - дробная часть числа x, f(x) = xx, f(x) = logx a.
1.3 Задачи для самостоятельного решения
1. Построить графики функций.
(a) f(x) = 2x 3; f(x) = jxj, f(x) = j2x + 2j;
(b) f(x) = 3(x 1)2 + 2, f(x) = x2 4x + 3, f(x) = 1 x2, f(x) = jx2 4j;
(c) f(x) = x3 x2 + x, f(x) = (x + 1)3 2, f(x) = 1 (x + 2)3, f(x) = jx3j;
(d) f(x) = x4, f(x) = x5; |
|
|
p |
|
|
|
|
p |
2 |
|
|
|||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
||||
|
p |
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
||
(e) f(x) = |
|
|
x, f(x) = |
|
x, f(x) = 1 x, f(x) = x |
8x 7; |
||||||||||||
(f) f(x) = |
|
1 |
|
, f(x) = |
1 |
, f(x) = |
x + 1 |
|
, f(x) = |
2x 1 |
; |
|
|
|||||
x2 |
x3 |
x 1 |
x + 1 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||
(g) f(x) = sin(x 2 ), |
f(x) = 2cos(x + |
3 ), f(x) = tg(x |
2 ), f(x) = 2ctg(x) 1; |
|||||||||||||||
(h) f(x) = arcsinx, f(x) = arccosx, f(x) = arctgx, f(x) = arcctgx; |
||||||||||||||||||
(i) f(x) = 2x, f(x) = (21 )x, f(x) = 3x+2, f(x) = 3x 1 + 2; |
2 (1 x) + 4; |
|
(j) f(x) = log2 x, f(x) = log2 |
x, f(x) = log3(x 1), f(x) = log |
|
1 |
|
1 |
2.Найдите область определения и область значений каждой из выше перечисленных функций.
3.Постройте графики следующих функций f(x) = [x], f(x) = fxg, f(x) = xx, f(x) = logx a, f(x) = logcos x sin x, f(x) = (sin x)ctgx, . Найдите область определения и область значений каждой из функций.
4. |
Даны функции f(x) = p |
|
, g(x) = x3. Выписать функции f g, g f, f f, g g. |
||||||||||||||
x |
|||||||||||||||||
5. |
Даны функции f(x) = x2, g(x) = log2x, h(x) = sin x. Выписать функции f g h, f h g, |
||||||||||||||||
|
h g h, h g g, g f f, f f g h. |
||||||||||||||||
1.4 |
Задачи домашней работы |
|
|
|
|
|
|
|
|
||||||||
1. |
Построить графики функций. |
|
|
|
|
|
|
|
|
||||||||
|
(a) y = 3x 2, y = 2jx + 2j 1, y = x2 5x + 6, y = j x2 + 7x 12j, y = x3 + x2 x 1. |
||||||||||||||||
|
|
2x + 3 |
1 |
|
|
p |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||
|
(b) y = |
|
|
, y = |
p |
|
, |
y = |
x |
|
x + 2; |
||||||
|
x 1 |
|
|||||||||||||||
|
|
x |
|
||||||||||||||
|
(c) y = 2 sin(x + 1) 3, y = tg2x, y = p |
|
, y = arcsin(1 x), y = arctg(x1 ); |
||||||||||||||
|
cos x |
||||||||||||||||
|
(d) y = 22 4x, y = (41 )x2 , y = log4(2 x), y = lnx, y = ep |
|
; |
||||||||||||||
|
x |
||||||||||||||||
2. |
Найти область определения и область значений, каждой функции из задачи 1. |
||||||||||||||||
3. |
Построить графики функций y = (cos x)x, y = (sin x)cos x, y = logsin x x, y = logx(cos x). |
||||||||||||||||
4. |
Даны функции f(x) = ln(x), g(x) = tgx. Выписать функции f g, g f, f f, g g f. |
||||||||||||||||

2Практическое занятие №2. Предел последовательности.
2.1Предел числовой последовательности
Определение 2. Числовой последовательностью называется функция an = f(n), определенная на множестве всех натуральных чисел.
Значения последовательности a1, a2,...,an,... называются ее членами. Последовательность an часто обозначают так: fang. Приведем примеры некоторых числовых последовательностей.
1.fng: 1; 2; 3; 4; :::;
2.f( 1)nng: 1; 2; 3; 4; :::;
3.n1 : 1; 12; 13; 14; :::;
4. |
n |
|
: |
1 |
; |
2 |
; |
3 |
; |
4 |
; :::; |
|||
|
|
|
|
|
|
|
|
|||||||
n + 1 |
2 |
3 |
4 |
5 |
||||||||||
|
|
|
|
|
|
|||||||||
5. ( 1)n |
n |
: |
1 |
; |
2 |
; |
3 |
; |
4 |
; :::; |
||
|
|
|
|
|
|
|
||||||
n + 1 |
2 |
3 |
4 |
5 |
||||||||
6. |
n + 1 |
: |
2 |
; |
3 |
; |
4 |
; |
5 |
; :::; |
||||
|
|
|
|
|
|
|
|
|||||||
n |
|
1 |
2 |
3 |
4 |
|||||||||
|
|
|
|
|
|
|||||||||
7. ( 1)n |
n + 1 |
: |
2 |
; |
3 |
; |
4 |
; |
5 |
; :::; |
||
|
|
|
|
|
|
|
||||||
n |
|
1 |
2 |
3 |
4 |
|||||||
8. |
2n + 1 |
: |
3 |
; |
5 |
; |
7 |
; |
9 |
; |
11 |
; :::; |
||||
|
|
|
|
|
|
|
|
|
|
|||||||
n |
1 |
2 |
3 |
4 |
5 |
|||||||||||
Для числовой последовательности, как и для любой функции, можно построить график. Он не является линией, а состоит из отдельных точек.
Определение 3. Число A называется пределом числовой последовательности fang, если для любого числа " > 0 существует такой номер N = N("), что для всех n > N выполня-
n!1
ется неравенство jan Aj < ". Это обозначают так: lim an = A или аn ! A.
n!1
Пример 2. Доказать, что lim 1 = 0.
n!1 n
Доказательство. Пусть " – произвольное положительное число. Запишем неравенство из
определения 3 для последовательности n1 , получим:
0 < ":
n
неравенство верно когда n > |
|
1 |
. Отсюда получаем, что в качестве N можно взять целую |
|||||||||||||
" |
||||||||||||||||
1 |
|
|
1 |
|
|
|
lim 1 |
|
||||||||
N |
|
|
|
|
|
|
= 0 |
|||||||||
часть числа |
|
, то есть |
|
= |
|
|
. Тем самым, из определения предела имеем n!1 |
|
|
. |
||||||
" |
|
" |
n |
|||||||||||||
Пример 3. Доказать, что |
lim |
1 |
= 0, где m и k – натуральные числа. |
|
||||||||||||
|
|
|
||||||||||||||
|
|
|||||||||||||||
m |
|
|
||||||||||||||
|
|
|
|
|
n!1 |
pnk |
|
|
|
|
||||||

Доказательство. Пусть " – произвольное положительное число. Запишем неравенство из
no
определения 3 для последовательности |
1 |
|
|
, получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
nk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
pnk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 < ": |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
k |
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Отсюда n > |
|
|
|
, то есть N = [p" |
|
]. Тем самым, из определения предела имеем lim |
m |
|
= |
||||||||||||||||||||||
0. |
pk "m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n!1 |
pnk |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема 1. Пусть lim an = A и |
lim bn = B. Тогда существуют пределы суммы an + bn, |
||||||||||||||||||||||||||||||
|
|
|
|
n!1 |
n!1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
an |
|
|
|
|||||
произведения anbn и при условии bn 6= 0 существует предел частного |
|
|
, причем |
|
|
|
|||||||||||||||||||||||||
bn |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
lim (an + bn) = A + B; |
|
|
lim (anbn) = AB; |
lim |
an |
= |
A |
: |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
n!1 |
|
|
|
|
n!1 |
|
|
|
|
|
n!1 bn |
B |
|
|
|
|||||||||||||
Пример 4. Вычислить предел последовательности |
lim |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n!1 n2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|
|
|
||||||||
Используя теорему 1 и пример 2, получаем nlim |
|
= nlim |
|
nlim |
|
= 0 0. |
|
|
|
||||||||||||||||||||||
n2 |
n |
n |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
!1 |
|
!1 |
|
!1 |
|
|
|
|
|
|
|
|
|
||||
Пример 5. Вычислить предел последовательности |
lim |
3n + 1 |
. |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n!1 n + 1 |
|
|
|
|
|
|
|
|||||||||
3n + 1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Имеем nlim |
|
|
|
|
= nlim 3 |
|
|
|
|
|
|
|
= nlim 3 2 nlim |
|
|
|
|
|
|
|
|
|
|
= 3 |
2 0 = 3. |
|||||||||||||||||||||||||||||||||||||||
n + 1 |
n + 1 |
|
n + 1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
!1 |
|
|
|
|
|
|
!1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
!1 |
|
!1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Пример 6. Вычислить предел последовательности |
|
lim |
3n2 + 2n 1 |
. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n!1 |
|
2n2 n + 4 |
|
|
|
|
|
|||||||||||||||||||||||
Вынесем в числителе и знаменателе n2 за скобки, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
lim |
n2(3 + n2 |
1 |
|
) |
= lim |
|
3 + n2 |
1 |
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
n2 |
n2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
n!1 n2(2 n1 + |
|
) |
|
|
n!1 2 n1 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
n2 |
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
Применяя теорему 1, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
3 + n |
|
|
|
|
n2 |
|
nlim 3 + nlim |
2 |
nlim |
1 |
|
|
|
|
|
3 + 0 |
|
|
0 |
|
3 |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
n |
n2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
lim |
|
|
|
2 |
|
1 |
|
|
= |
!1 |
|
|
|
!1 |
|
|
!1 |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
: |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
n1 + |
4 |
|
|
|
|
|
|
2 0 + 0 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
n!1 2 |
|
|
|
|
lim 2 |
|
lim |
+ lim |
|
|
|
|
|
|
|
|
2 |
||||||||||||||||||||||||||||||||||||||||||||||
|
n2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n!1 |
|
|
|
n!1 n |
n!1 n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Пример 7. Вычислить предел последовательности |
|
lim |
3n2 + 2n 1 |
. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n!1 |
|
2n3 n + 4 |
|
|
|
|
|
|||||||||||||||||||||||
Вынесем в числителе и знаменателе n3 за скобки, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
lim |
n3(n3 + |
2 |
|
|
1 |
|
) |
= lim |
|
n3 + |
2 |
|
|
|
1 |
|
: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
n2 |
n3 |
|
n2 |
n3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
4 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
n!1 n3(2 |
+ |
) |
|
|
n!1 2 |
+ |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
n2 |
n3 |
|
|
n2 |
n3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
Применяя теорему 1, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
n + n2 |
|
|
n3 |
|
|
|
|
|
3 |
|
+ nlim |
2 |
|
nlim |
1 |
|
|
|
|
|
|
0 + 0 |
|
|
0 |
|
|
0 |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
nlim n |
|
|
n2 |
n3 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
lim |
3 |
|
|
2 |
|
1 |
|
= |
|
!1 |
|
|
|
|
|
!1 |
|
|
|
|
|
!1 |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
= 0: |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
n!1 2 n1 + |
|
|
|
|
|
|
|
lim 2 |
|
|
|
lim |
|
+ lim |
|
|
|
|
|
|
|
|
2 0 + 0 |
|
2 |
|
||||||||||||||||||||||||||||||||||||||
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n!1 |
n!1 n2 |
n!1 n3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||

Пример 8. Вычислить предел последовательности lim |
n3 + 1 |
. |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n!1 |
4n2 + 3 |
|
|
|
|||||||
Вынесем в числителе и знаменателе n3 за скобки, имеем |
|
|
|
|||||||||||||||||||||
|
3 |
1 |
|
|
|
1 |
|
|
|
lim |
1 + lim |
1 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
n (1 + |
|
|
) |
|
1 + |
|
|
|
|
= |
n!1 |
|
|
n!1 n3 |
|
1 |
|
||||||
lim |
n3 |
= lim |
n3 |
|
|
= |
: |
|||||||||||||||||
|
|
3 |
|
|
|
3 |
|
|
|
|
||||||||||||||
n!1 n3(n4 + |
) |
n!1 n4 + |
|
|
lim |
4 |
|
+ lim |
3 |
|
|
0 |
|
|||||||||||
n3 |
n3 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n!1 n |
n!1 n3 |
|
|
|
|||||||
Получили деление на 0. Не совсем так. Мы делим число очень близкое к 1 на число очень
близкое к 0, но не на 0. Поэтому |
1 |
! 1. То есть, |
|
|
|
|
|
|
|
|
|
|
||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
nlim |
n3 + 1 |
|
|
= 1: |
|
|
|
|
|
|
|
|
|||||||
|
|
|
4n2 + 3 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
!1 |
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
+ p4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 9. Вычислить предел последовательности nlim |
n |
n |
. |
|||||||||||||||||||
|
p3 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
!1 |
|
|
|
n + 1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
Вынесем за скобки в числителе и знаменателе n2 , получим: |
|
|||||||||||||||||||||
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
n2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
(1 + pn ) |
|
|
1 |
|
|
|
|
|
|
|||||||||
lim |
|
|
|
|
|
|
|
|
|
|
= |
|
= |
: |
|
|
|
|
|
|||
|
|
1 |
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|||||||
n!1 n2 (n |
6 + n |
2 ) |
|
0 |
|
|
|
|
|
|
||||||||||||
2.2Задачи для самостоятельного решения
Напишите несколько первых членов следующих последовательностей. Определите, являются ли они ограниченными сверху, ограниченными снизу, возрастающими, убывающими?
1. |
|
2n |
; |
|
|
|
|
|
|
|
|
|
n2 + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
; |
|
|
|
|
7. |
|
|
|
n! |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
f |
g |
|
|
|
|
|
|
|
|
3. |
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
5. |
|
|
|
|
|
|
|
|
|
|
f |
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
2. |
f( 1)ng; |
4. |
2n |
+13 ; |
|
|
|
|
|
|
|
|
|
|
6. |
|
n2 + 2n + 2 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n + 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Докажите, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
n + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1. |
lim |
|
|
|
|
= 0; |
|
|
|
|
|
3. |
|
lim |
= 1; |
|
|
|
|
|
|
|
5. |
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
= 0. |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
n!1 n + 1 |
|
|
|
|
|
n!1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n!1 n3 + 2n2 n + 3 |
|||||||||||||||||||||||||||||||||||||||
2. |
nlim ( 1)n |
|
n |
= 0; |
|
|
|
4. |
nlim |
2n + 1 |
= 2; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
n + 1 |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
!1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
!1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Вычислите пределы последовательностей. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
3n 1 |
|
|
|
|
|
|
|
|
4n3 n2 n + 2 |
|
|
|
|
|
|
p |
|
|
|
|
|
|
+ p |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
1. |
lim |
|
. |
|
|
|
|
5. |
|
lim |
. |
|
|
|
|
|
2n + 1 |
3 + n |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9. |
nlim |
|
|
|
|
|
p |
|
|
|
|
|
|
. |
|
|
|
||||||||||||||||||||
|
n |
!1 |
|
2n + 2 |
|
|
|
|
|
n |
!1 |
|
|
n2 |
|
2n + 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
!1 |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
n |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
n + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
2. |
lim |
|
+ 3n 1 |
. |
|
|
|
6. |
|
lim |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
lim |
pn + pn |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
n |
!1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
n |
!1 |
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
10. |
n |
|
4 |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
2n n + 3 |
|
|
|
|
|
|
|
2 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
!1 pn pn |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
p3 |
|
|
+ p4 |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
lim |
|
|
|
4n + 3 |
|
|
|
|
7. |
|
lim |
|
|
|
. |
|
|
|
|
|
|
lim |
n 1 |
n + 1 |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
3. |
n |
!1 n |
2 |
3n + 5 |
. |
|
|
|
|
n |
!1 |
|
|
|
|
pn |
+ 1 |
|
|
|
|
|
11. |
n |
!1 |
p3 |
|
|
|
|
|
|
|
|
|
|
|
p5 |
. |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 3 |
|
|
|
|
|
|
|
|
|
|
|
2n 1 + |
2n + 1 |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
p |
|
+ p |
|
+ 3n |
. |
||||||||||||||||||||||||||||||||||||||||||
4. |
lim |
|
4n3 n2 n + 2 |
|
|
|
8. |
|
lim |
2n 1 |
+ 3 |
. |
|
|
|
|
12. |
lim |
3n 1 |
2n + 3 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
n2 2n + 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
n!1 |
|
|
|
|
|
|
n!1 p2n + 1 2 |
|
|
|
|
|
|
n!1 |
|
|
|
|
|
|
npn 4 |
||||||||||||||||||||||||||||||||||||||||||||||

2.3Задачи домашней работы
Докажите, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1. |
lim |
2n + 1 |
= |
1 |
. |
|
|
|
|
3. |
lim |
n2 1 |
|
= |
1. |
||||||||||
4n |
|
|
|
|
|
|
|
||||||||||||||||||
|
n |
!1 |
1 2 |
|
|
|
|
|
n |
!1 |
2n + 1 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2. |
lim |
3n2 n + 2 |
|
= |
3 |
. |
4. |
lim |
n 1 |
= 0. |
|||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
n!1 |
2n2 3n + 1 2 |
|
n!1 |
2n2 + 1 |
|
|
|
|||||||||||||||||
Вычислите пределы последовательностей. |
|
|
|
|
|||||||||||||||||||||
|
|
2n2 + 3n 1 |
|
|
|
|
|
|
n2p |
|
|
. |
|
|
|
|
|||||||||
1. |
lim |
. |
|
|
|
4. |
lim |
n |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
n!1 |
|
n + 1 |
|
|
|
|
n!1 n3 2 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. |
lim |
1 |
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2. |
lim |
3n3 + n 1 |
. |
|
|
|
|
n!1 |
2n + 1 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
2n2 + n 1 |
|
||||||||||||||||||
|
n!1 |
|
n3 2 |
|
|
|
6. |
lim |
: |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n!1 n2 + 4n + 5 |
|
|||||||||
3. |
lim |
3n2 + 5n 4 |
. |
|
|
|
7. |
lim |
n3 + n2 + 6 |
: |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
n2 + 3 |
|
|
|||||||||||||
|
n!1 |
|
n3 2 |
|
|
|
|
n!1 |
|
|
|
||||||||||||||
8. lim n4 + n5 :
n!1 n2 + n3
9. lim
n!1
10. lim
n!1
pp
2n 4 + |
n + 6 |
|||
p |
|
1 |
|
. |
n |
|
|||
p |
|
|
+ p |
|
|
|
n3 + 2n + 2 |
|
|||||
3n 2 |
. |
|||||
|
p |
|
|
|||
|
n n 1 2n |
|
||||
3Практическое занятие № 3. Предел функции.
3.1Предел функции
Определение 4. Пределом функции f(x) при стремлении x к x0 называется число A, если для любого числа " > 0 существует такое число (") > 0, что для всех x, для которых выполняется условие 0 < jx x0j < , выполняется неравенство jf(x) Aj < ".
Записывают следующим образом: lim f(x) = A. Число A есть предел функции f(x) в
точке x = x0. Оно означает, что для всех x достаточно близких к x0, соответствующие значения f(x) будут сколь угодно близкими к A.
Пример 10. Доказать, что lim x2 = 4.
x!2
Пусть " > 0 - произвольное положительное число. Необходимо найти такое число > 0,
что для любых x, удовлетворяющих неравенству 0 < |
j |
x |
|
2 |
j |
< , выполняется неравенство |
|||||||||||||||||||||||||||||||||||||||||
jx |
2 |
4j |
< ". jx |
2 |
4j |
= |
jx 2jjx + 2j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
< ". Оценим jx + 2j. jx + 2j = j(x 2) + 2j. Тогда |
|||||||||||||||||||||||||||||||||||||||||||||
по2 |
свойству модуля имеем j(x 2) + 2j jx 2j + j2j < + 2: Таким образом, получаем, |
||||||||||||||||||||||||||||||||||||||||||||||
j |
x |
|
|
4 |
j |
= |
j |
x |
|
2 x + 2 |
j |
< ( + 2): Чтобы это неравенство выполнялось необходимо,чтобы |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
jj |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
= 4: |
|||||||
( + 2) = ". Из этого равенства мы найдем . Следовательно, мы доказали, что lim x |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x!2 |
|
|
Теорема 2. Предел постоянной величины равен самой постоянной: lim C = C: |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Теорема 3 (Свойства пределов). Если функции f(x) |
|
|
|
|
|
|
|
|
|
|
|
x!x0 |
|
|
|||||||||||||||||||||||||||||||||
|
и g(x) имеют пределы при x ! x0, |
||||||||||||||||||||||||||||||||||||||||||||||
то имеют пределы при |
|
! |
|
0 и функции |
|
|
|
|
|
|
|
), |
|
|
|
|
|
|
|
|
), |
f(x) |
|
|
|||||||||||||||||||||||
x |
x |
f |
( |
x |
) + |
g x |
f |
( |
x |
g |
x |
|
lim g(x) = 0: |
||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
( |
|
|
|
|
) |
( |
|
g(x) , если x!x0 |
|
6 |
|||||||||||||||||||||||||||||||||
Причем эти пределы равны: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim (f(x) + g(x)) = lim f(x) + lim g(x): |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x!x0 |
|
|
|
|
|
|
|
|
|
x!x0 |
|
|
|
|
x!x0 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim (f(x)g(x)) = lim f(x) lim g(x): |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x!x0 |
|
|
|
|
|
|
|
x!x0 |
|
x!x0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(x) |
|
|
|
|
lim f(x) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
= |
x!x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g |
x |
|
|
|
lim g(x): |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
! |
x0 |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
x |
x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
!
