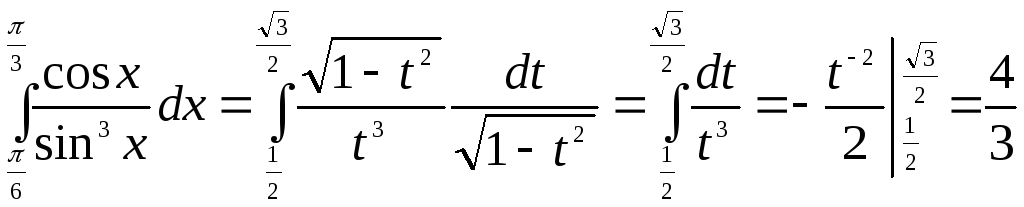- •« Пособие по математическому анализу для студентов лечебного и педиатрического факультетов медицинской академии » Ярославль
- •Содержание.
- •Введение.
- •1. Множество и функция.
- •2. Производная функции.
- •2.1 Определение производной функции одной переменной.
- •Таким образом:
- •Геометрический смысл производной.
- •Физический смысл производной.
- •Производная сложной функции.
- •Элементарных функций.
- •Примеры дифференцирования простых и сложных функций.
- •Приближенное значение функции при малых значениях аргумента.
- •2.7. Производные и дифференциалы высших порядков.
- •Найдем явное выражение для второго дифференциала. По определению дифференциала имеем:
- •Неопределенный интеграл.
- •Определение неопределенного интеграла.
- •Свойства неопределенного интеграла.
- •Основные методы интегрирования.
- •Метод интегрирования по формулам.
- •Метод замены переменных.
- •3.4.3. Примеры нахождения неопределенного интеграла.
- •1 Способ.
- •2 Способ.
- •Определенный интеграл.
- •Определение определенного интеграла.
- •Свойства определенного интеграла.
- •4.3. Формула Ньютона-Лейбница.
- •4.4. Замена переменной в определенном интеграле.
- •Алгоритм нахождения определенного интеграла методом замены переменной.
- •4.5. Примеры нахождения определенного интеграла.
- •Дифференциальные уравнения.
- •Основные понятия о дифференциальных уравнениях.
- •5.2. Уравнения с разделяющимися переменными.
- •5.3. Примеры составления и решения дифференциальных уравнений.
- •5.3.1. Закон радиоактивного распада в дифференциальной и интегралной формах.
- •Примеры решения дифференциальных уравнений методом разделения переменных.
- •6. Литература.
4.4. Замена переменной в определенном интеграле.
Замена переменной в определенном интеграле позволяет сначала найти неопределенный интеграл, а затем, воспользовавшись формулой Ньютона-Лейбница, найти определенный интеграл.
Пусть
функция f(x)
непрерывна на отрезке a;
b,
функция x
= (t)
имеет на отрезке а;b
непрерывную производную, при этом
![]() и
и![]() .
Тогда:
.
Тогда:
![]()
Данная формула называется формулой замены переменной в определенном интеграле или формулой подстановки.
Если при вычислении неопределенного интеграла с помощью замены переменной необходимо от новой переменной t возвращаться к старой переменной х, то при вычислении неопределенного интеграла этого делать не надо.
Алгоритм нахождения определенного интеграла методом замены переменной.
Алгоритм нахождения определенного интеграла методом замены переменной состоит из следующих шагов.
1. Подберем такую переменную x = (t), которая сведет первоначальный интеграл к табличному виду.
2. Заменим старые пределы интегрирования на новые. Для этого равенство x = (t) разрешается относительно t:
t= ψ(x).
Нижний предел интегрирования равен α=ψ(a). Верхний предел интегрирования равен β=ψ(b).
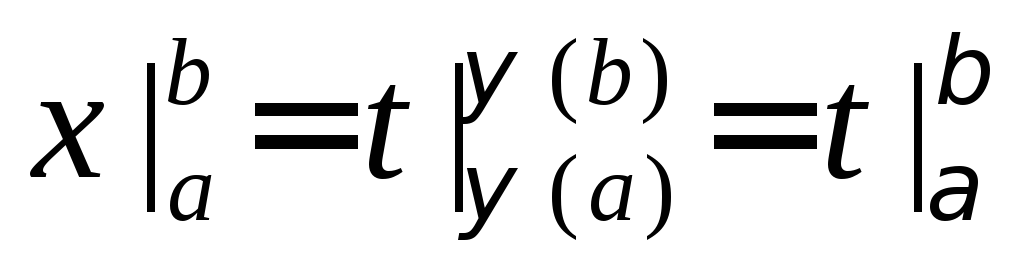
Таким образом, вместе с заменой переменной в первоначальном интеграле меняются и пределы интегрирования. Первоначальный определенный интеграл свелся к табличному интегралу относительно t:
![]()
3. Пусть его первообразная равна F(t), на основании формулы Ньютона – Лейбница можно написать:
F(t)![]()
![]() =
F(β)
– F(α).
=
F(β)
– F(α).
Первоначальный интеграл найден.
Приведем полную последовательность вычислений:
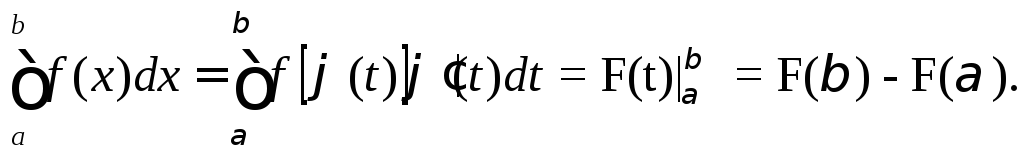
Следует обратить внимание на то, что в первообразной F(t) нет необходимости возвращаться к первоначальной переменной х ( t= ψ(x), F(ψ(x) ). Возврат к первоначальной переменной приведет к необходимости вернуться к старым пределам интегрирования. Это не ошибка – просто увеличится объем вычислений.
4.5. Примеры нахождения определенного интеграла.
1.
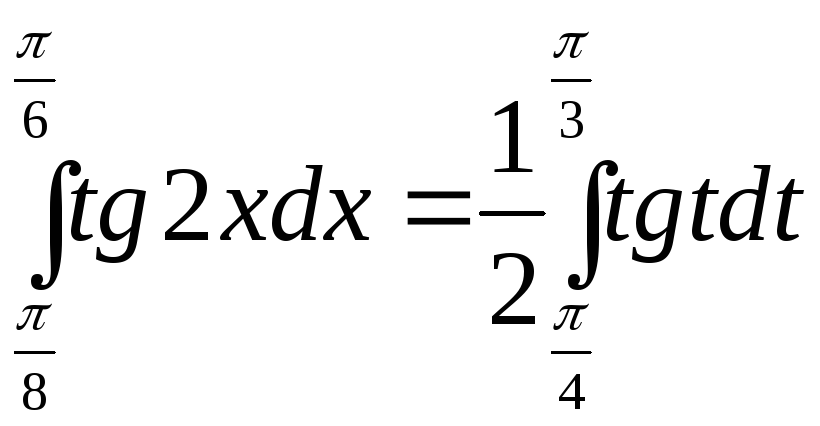 =
=
1.1.
Возьмем новую переменную:
![]() ,
,
выражаем старую переменную через новую:
![]()
1.2.
По определению дифференциала: ![]()
1.3.
Делаем замену пределов интегрирования: 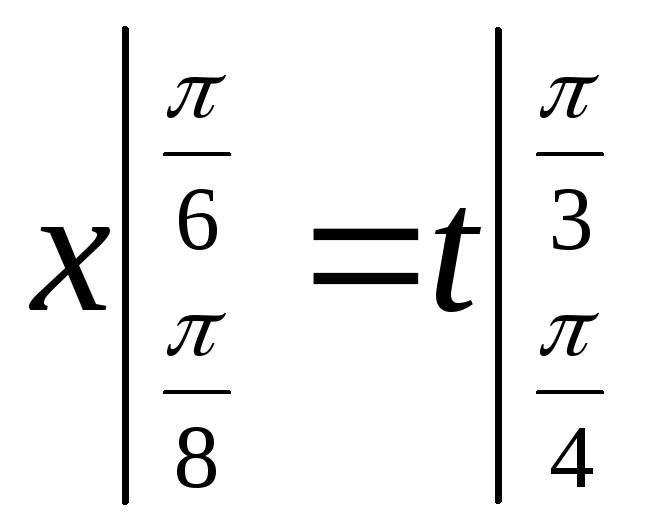 (1)
(1)
Замена пределов интегрирования происходит следующим образом.
Для старой переменной х нижний предел интегрирования равен /8, но так как t = 2x, для t нижний предел равен:
![]()
Для старой переменной х верхний предел интегрирования равен /6, но так как t = 2x, верхний предел интегрирования для t равен
![]()
=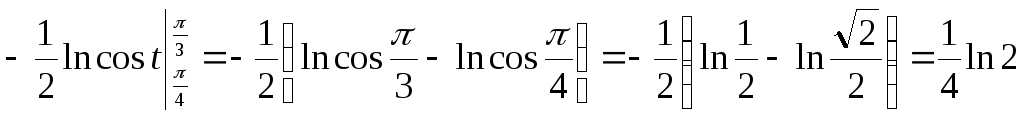
Практически замену пределов интегрирования удобно делать через условное равенство (1).
2.
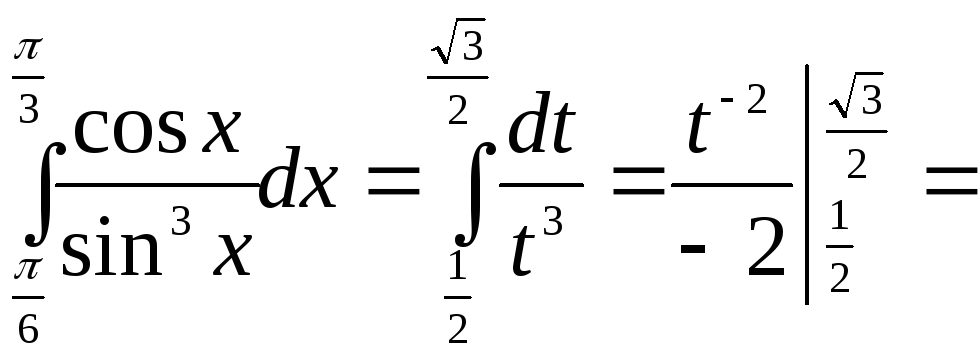
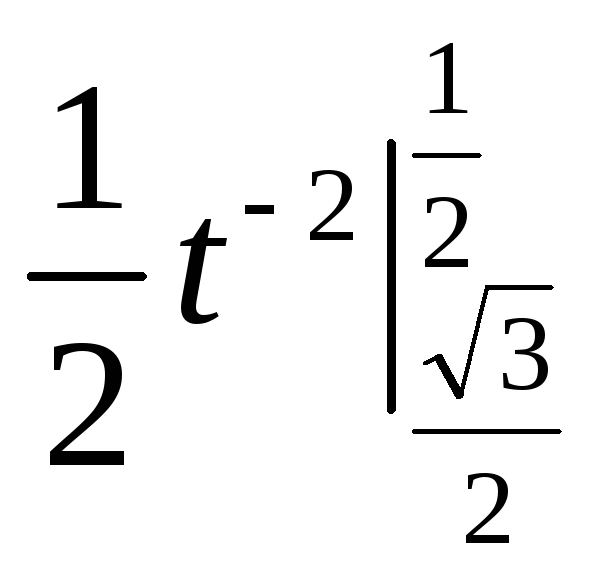 =
=![]()
1 способ.
t = sinx
dt = cosx dx
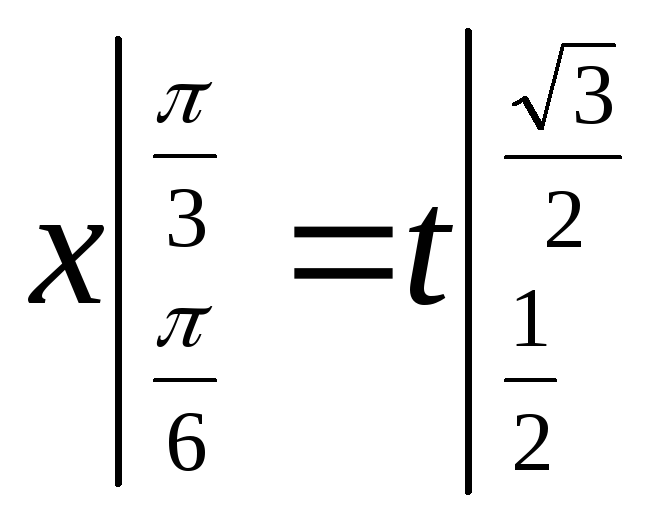
2 способ.
t = sinx
x = arcsin t
dx
= (arcsin t)dt
=
![]()
sin2 x + cos2 x = 1
cos2 x = 1 – sin2 x = 1 – t2
cosx
=
![]()