1 Способ.

1. = -

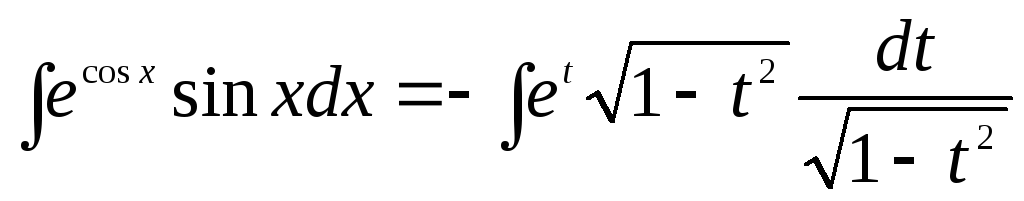1.1. Делаем замену переменных: t = cos x

1.2. Выражаем старую переменную через новую: x = arccos t

1.3. По определению дифференциала:

dx = (t)dt = (arccos t )′ dt =

dx=

1.4. sin²x + cos²x = 1, т.к. t = cos x, то sin²x + t² = 1,

sin x =

1.5. Заменяем в первоначальном интеграле cos x, sin x, dx через t.

1.6. Первоначальный интеграл свелся к табличному относительно t. Найти интеграл относительно t .

1.7. При использовании метода подстановки надо помнить, что после взятия неопределенного интеграла необходимо возвращаться от новой переменной t к первоначальной переменной x. Возвращаемся от переменной t к переменной х.

2 Способ.

2.

2.1. Вводим переменную t = cos x

2.2. Берем дифференциал от обеих частей и находим dx:

dt = - sin x dx

sin x dx = - dt

dx = - dt / sin x

2.3. Подставляем вместо cos x и dx их выражения через t в первоначальный интеграл и сводим его к табличному.

2. Определенный интеграл.

1. Определение определенного интеграла.

Пусть на отрезке а; в определена непрерывная функция f(x). Отрезок а; в разобьем на частичные отрезки x = x_i+1- x_i. Выберем на каждом отдельном отрезке x_i произвольным образом точку _i и составим сумму:

S =

Если существует предел

I=, то функция f(x) называется интегрируемой на отрезке а; в, а число I называется определенным интегралом функции f(х) на отрезке а; в и обозначается символом:

По определению функция f(x) называется подинтегральной функцией, f(x)dx – подынтегральным выражением, a и b – пределы интегрирования (a – нижний предел, b – верхний предел).

Геометрически определенный интеграл представляет собой площадь криволинейной трапеции, ограниченной сверху графиком функции y=f(x), снизу – отрезком a; b оси ОХ, с боков отрезками прямых х =а и х = b.

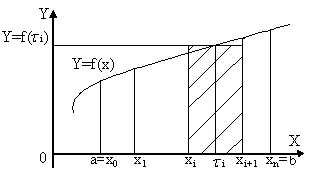
Рис. 2

2. Свойства определенного интеграла.

1. Определенный интеграл от функции с равными пределами равен 0.

2. Постоянный множитель можно выносить за знак определенного интеграла:

3. Интеграл по отрезку a; b равен сумме интегралов по частям данного отрезка:

4. При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный:

5. Определенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций в отдельности:

5. Если f(x)0 на отрезке a; b, то

0. 4.3. Формула Ньютона-Лейбница.

Если функция f(x) непрерывна на отрезке a; b и F(x) – первообразная функции f(x) на этом отрезке, то:

Данная формула называется формулой Ньютона-Лейбница. Она устанавливает теоретическую связь между определенным и неопределенным интегралом и дает удобное практическое правило вычисления определенного интеграла. Для краткости записи употребляется обозначение:

F(b) – F(a) = F(x)

поэтому формула Ньютона-Лейбница принимает вид: