2.3. Принадлежность точки и прямой плоскости

Признаки принадлежности хорошо известны из курса планиметрии. Наша задача рассмотреть их применительно к проекциям геометрических объектов.

Точка принадлежит плоскости, если она принадлежит прямой, лежащей в этой плоскости.

Принадлежность прямой плоскости определяется по одному из двух признаков:

а) прямая проходит через две точки, лежащие в этой плоскости;

б) прямая проходит через точку и параллельна прямой, лежащим в этой плоскости.

Используя эти свойства, решим в качестве примера задачу. Пусть плоскость задана треугольником АВС. Требуется построить недостающую проекцию D₁ точки D, принадлежащей этой плоскости. Последовательность построений следующая (рис. 2.5).

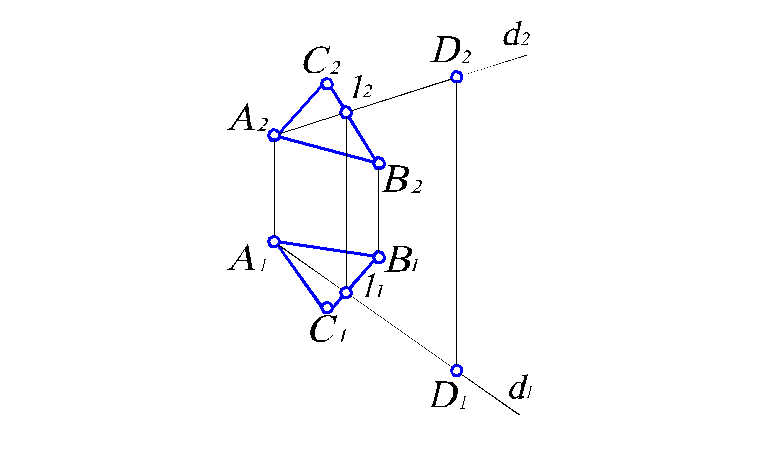
Рис. 2.5. К построению проекций точки, принадлежащей плоскости

Через точку D₂ проводим проекцию прямой d, лежащей в плоскости АВС, пересекающую одну из сторон треугольника и точку А₂. Тогда точка 1₂ принадлежит прямым А₂D₂ и C₂В₂. Следовательно, можно получить ее горизонтальную проекцию 1₁ на C₁В₁ по линии связи. Соединив точки 1₁ и А₁, получаем горизонтальную проекцию d₁. Ясно, что точка D₁ принадлежит ей и лежит на линии проекционной связи с точкой D₂.

Достаточно просто решаются задачи на определение принадлежности точки или прямой плоскости. На рис. 2.6 показан ход решения таких задач. Для наглядности изложения задачи плоскость задаем треугольником.

Рис. 2.6. Задачи на определение принадлежности точки и прямой плоскости.

Для того, чтобы определить принадлежит ли точка Е плоскости АВС, проведем через ее фронтальную проекцию Е₂ прямую а₂. Считая, что прямая а принадлежит плоскости АВС, построим ее горизонтальную проекцию а₁ по точкам пересечения 1 и 2. Как видим (рис. 2.6, а), прямая а₁ не проходит через точку Е₁. Следовательно, точка Е АВС.

В задаче на принадлежность прямой в плоскости треугольника АВС (рис. 2.6, б), достаточно по одной из проекций прямой в₂ построить другую в₁* считая, что вАВС. Как видим, в₁* и в₁ не совпадают. Следовательно, прямая в  АВС.

2.4. Линии уровня в плоскости

Определение линий уровня было дано ранее. Линии уровня, принадлежащие данной плоскости, называются главными. Эти линии (прямые) играют существенную роль при решении ряда задач начертательной геометрии.

Рассмотрим построение линий уровня в плоскости, заданной треугольником (рис. 2.7).

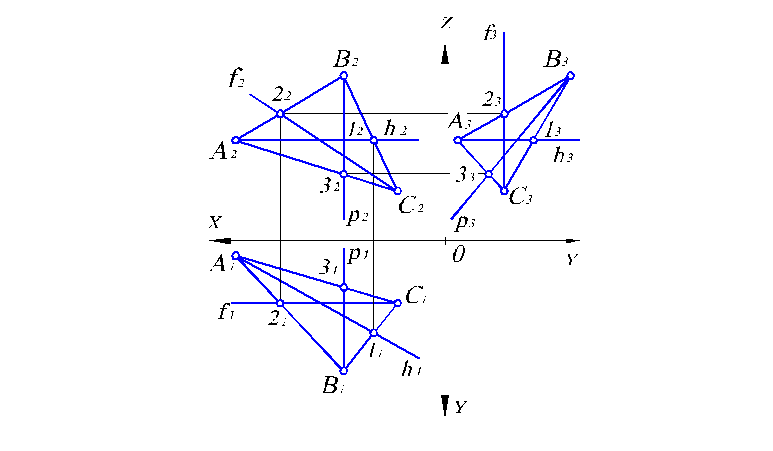
Рис. 2.7. Построение главных линий плоскости, заданной треугольником

Горизонталь плоскости АВС начинаем с вычерчивания ее фронтальной проекции h₂, которая, как известно, параллельна оси ОХ. Поскольку эта горизонталь принадлежит данной плоскости, то она проходит через две точки плоскости АВС, а именно, точки А и 1. Имея их фронтальные проекции А₂ и 1₂, по линии связи получим горизонтальные проекции (А₁ уже есть) 1₁. Соединив точки А₁ и 1₁, имеем горизонтальную проекцию h₁ горизонтали плоскости АВС. Профильная проекция h₃ горизонтали плоскости АВС будет параллельна оси ОХ по определению.

Фронталь плоскости АВС строится аналогично (рис. 2.7) с той лишь разницей, что ее вычерчивание начинается с горизонтальной проекции f₁, так как известно, что она параллельна оси ОХ. Профильная проекция f₃ фронтали должна быть параллельна оси ОZ и пройти через проекции С₃, 2₃ тех же точек С и 2.

Профильная линия плоскости АВС имеет горизонтальную р₁ и фронтальную р₂ проекции, параллельные осям OY и OZ, а профильную проекцию р₃ можно получить по фронтальной, используя точки пересечения В и 3 с  АВС.

При построении главных линий плоскости необходимо помнить лишь одно правило: для решения задачи всегда нужно получить две точки пересечения с данной плоскостью. Построение главных линий, лежащих в плоскости, заданной иным способом, ничуть не сложнее рассмотренного выше. На рис. 2.8 показано построение горизонтали и фронтали плоскости, заданной двумя пересекающимися прямыми аив.

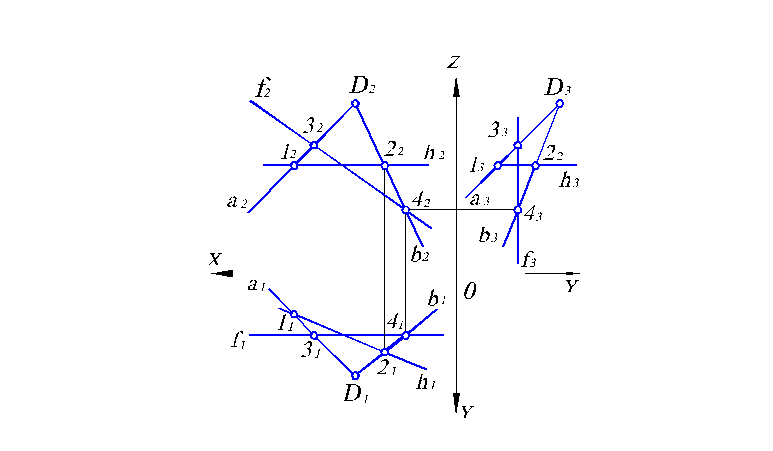
Рис. 2.8. Построение главных линий плоскости, заданной пересекающимися прямыми.