2.6. Графическое решение позиционных и метрических задач

Позиционные задачи на плоскости

Позиционными называются задачи на определение каких-либо общих элементов геометрических объектов, например, точкипересечения прямой и плоскости,линиипересечения двух плоскостей.

Пересечение прямой и плоскости

Задачу на пересечение прямой и плоскости можно решать с помощью вспомогательной секущей плоскости, которая должна удовлетворять следующим условиям:

— быть плоскостью частного положения, так как именно плоскость частного положения проецируется на соответствующую плоскость проекций в виде прямой;

— проходить через прямую, точку пересечения которой с плоскостью мы отыскиваем.

Рассмотрим сначала частный случай.

Пусть плоскость занимает частное положение в пространстве, например, является горизонтально-проецирующей и задана треугольником АВС (рис. 2.12, а). Необходимо найти точку пересечения ее с прямой а, заданной произвольно. Поскольку на П₁горизонтально–проецирующая плоскость вырождается в прямую₁, то горизонтальной проекцией точки пересечения будетК₁. Далее по линии связи на прямойа₂ (очевидно точка пересеченияКпринадлежит прямой а) найдем фронтальную проекциюК₂точки пересечения.

Осталось определить видимые участки прямой а, поскольку наП₂часть указанной прямой будет закрыта от наблюдателя плоскостьюАВС. Для этого необходимо рассмотреть точку, где пересекаются фронтальные проекцииаи какой-либо прямой ( например,АС ), лежащей в плоскостиАВС. Обозначим эту точку 1₂. Но пересекаться прямая а иАВСмогут только в одной точке, которую мы отыскали (К₂). Все остальные точки будут точками, где они скрещиваются. Следовательно, прямаяаиАСскрещиваются в пространстве. Значит, все точки, где пересекаются их проекции, будут конкурирующими, а именно 1₂=2₂. Тогда наП₁ имеем по линии связи 1₁А₁С₁и 2₁а₁. Видимой является точка 2, которая принадлежит прямойа. Это сохраняется до точки пересеченияК₂. Затем, естественно, участок прямойабудет невидим (обозначается пунктирной линией) до выхода из-под плоскостиАВС. Теперь задачу можно считать полностью решенной.

Рис. 2.12. Пересечение прямой и плоскости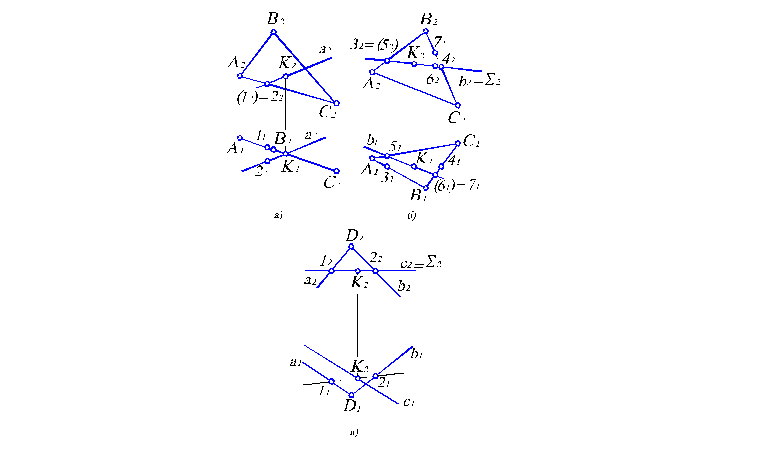

Рассмотрим общий случай.

Пусть плоскость задана треугольником АВС. Здесь и в дальнейшем используем задание плоскости в основном треугольником, так как в этом случае решение задачи наиболее наглядно. Необходимо найти точку пересечения произвольно заданной прямойвсАВС(рис. 2.12, б).

Как указано выше, нужно через прямую впровести плоскость частного положения (например, фронтально-проецирующую). Линия пересечения этой плоскости совпадает с прямойвнаП_2, т.е.₂=в₂ . Тогда по точкам пересечения 3₂и 4₂построим точки 3₁и 4₁, а следовательно, и прямую 3₁4₁, являющуюся горизонтальной проекцией линии пересечения плоскостии АВС. Но так как прямая 34АВС, то точка К₁будет горизонтальной проекцией точки пересечения прямойвиАВС.По ней найдем и фронтальную проекциюК₂, которая, очевидно, должна быть расположена нав₂(ведь точка пересечения принадлежит и прямойвиАВС ).

Определим видимые участки прямой в на обеих проекциях по конкурирующим точкам. Для определения видимости на П₂ используем фронтально-конкурирующие точки (например, точки 3₂=5₂, где скрещиваются в₂ и А₂В₂). Очевидно, что точка 3₁ ближе к нам, чем точка 5₁. Следовательно, на П₂ выше 3₂, тогда в этой точке А₂ В₂ выше, а в₂ лежит под ней. Это верно только до точки пересечения К₂. Далее, естественно, выше будет в₂. Аналогично по горизонтально–конкурирующим точкам (например, 6₁=7₁) определяем, что в точках 6₁=7₁ прямая В₁С₁ лежит выше, чем в₁, так как точка 7₂ расположена выше, чем точка 6₂. Невидимый участок прямой в обозначаем пунктирной линией.

Следует иметь в виду, что когда плоскость задана не плоской фигурой, можно говорить лишь о видимости отдельных участков прямой относительно плоскости, хотя такая постановка задачи верна и в случае плоской фигуры.

Предыдущую задачу можно сформулировать несколько иначе: определить видимость участков прямой в относительно точки ее пересечения с плоскостью, которая задана АВС, а не с самим треугольником АВС. Тогда невидимые участки левее точки К₂ и правее К₁ мы должны были бы продлить до бесконечности.

Более наглядно эту особенность можно проинтерпретировать на примере (рис. 2.12, в), где плоскость задана пересекающимися прямыми а и в. Ход решения ничем не отличается от предыдущего, но невидимость участков прямой с уже не ограничена геометрическими элементами, задающими плоскость.

Таким образом, чем бы ни была задана плоскость, точку ее пересечения с прямой можно найти, используя секущую плоскость частного положения, проходящую через эту прямую, а видимость (или невидимость) на плоскостях проекций отдельных участков прямой – с помощью конкурирующих точек.

Метрические задачи на плоскости

Метрическиминазываютсязадачипо определению натуральной величины геометрических объектов (отрезка прямой или плоскости), либо кратчайшего расстояния между геометрическими объектами. Наиболее универсальным для решения таких задач принято считатьспособ замены плоскостей проекций, который заключается в следующем: оставляют неизменным положение в пространстве геометрического объекта, а заменяют одну или последовательно обе плоскости проекций так, чтобы интересующие нас прямые или плоскости оказались параллельными одной из новых плоскостей проекций.

Тогда одна из основных плоскостей проекций П₁илиП₂заменяется новой плоскостью проекцийП₄, подходящим образом расположенной относительно изображаемого геометрического объекта, но перпендикулярной незаменяемой плоскости проекций.

В результате замены одной из основных плоскостей на плоскость проекций П₄получаем вместо старой системы плоскостей проекцийП₁/П₂новую системуП₁/П₄ (рис. 2.15), если заменялась плоскостьП₂, и системуП₂/П₄, если заменялась плоскостьП₁.

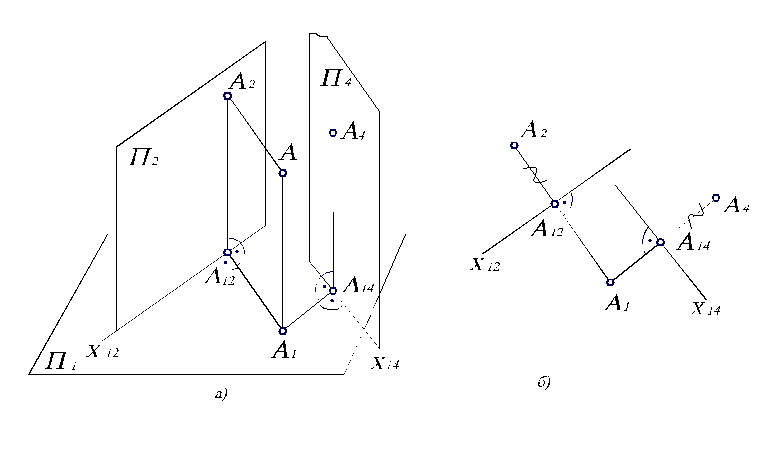
Рис. 2.13. Интерпретация способа замены плоскостей проекций

Например, на рис. 2.15, а плоскость П₄может выступать в роли фронтальной плоскости проекцийП₂. На рисунке 4.5, б, фигурными скобками отмечены расстояния от точкиАдо горизонтальной плоскости проекцийП₁. Естественно, как видно на рис. 2.15, а, эти расстояния равныА₂А₁₂=А₄А₁₄, так как высота точкиАнад плоскостьюП₁проецируется как наП₂, так и наП₄в виде одинаковых отрезков. Расстояние же доП₂иП₄от точкиАмогут быть различными, поэтомуА₁А₁₂А₁А₁₄.

Способ замены плоскостей проекций рационально применять при решении следующих задач:

• определение натуральной величины отрезка прямой линии;

• определение натуральной величины плоской фигуры;

• определение натуральной величины двугранного угла;

• определение кратчайшего расстояния от точки до прямой линии или до плоскости;

• определение кратчайшего расстояния между двумя параллельными или двумя скрещивающимися прямыми;

Решение задач данным способом рассмотрим на нескольких примерах.

Определение длины отрезка прямой общего положения

Для определения натуральной величины (длины) отрезка АВпрямой линии необходимо сделать этот отрезок прямой линии общего положения в новой системе плоскостей проекций линией уровня. Чтобы отрезокАВстал линией уровня относительно новой плоскости проекций, заменим плоскостьП₂на плоскостьП₄, параллельнуюАВ, и перейдем от системыП₁/П₂к системеП₁/П₄. Новую ось проекцийX₁₄, выбираем параллельноА₁В₁ (рис. 2.16). Для построения новой проекции отрезкаАВпроводим новые линии проекционной связи перпендикулярно осиХ₁₄, и отмечаем на них новые проекцииА₄,В₄точекАиВ. Для этого откладываемА_х1А₄=А₂А_х,В_х1В₄=В₂В_х.

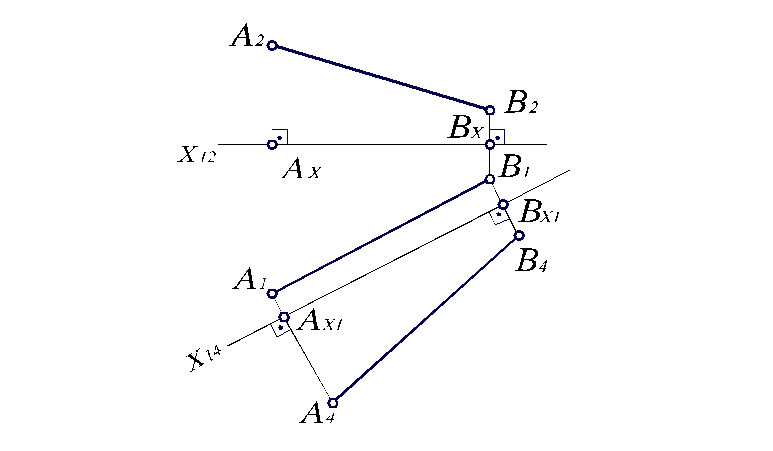
Рис. 2.14. Преобразование прямой общего положения в прямую уровня.

Соединяя найденные точки А₄,В₄, получаем новую проекциюА₄В₄отрезкаАВ. Как видим, отрезокАВв новой системе плоскостей проекцийП₁/П₄является линией уровня, так какА₁В₁ параллельнаX₁₄, а следовательно,АВпараллельнаП₄. Тогда, очевидно, чтоА₄В₄является натуральной величиной отрезкаАВ.

Определение натуральной величины плоской фигуры

Для определения натуральной величины плоской фигуры необходимо дополнительную плоскость построить так, чтобы она была параллельна рассматриваемой фигуре, и тогда на эту плоскость проекций плоская фигура проецируется в натуральную величину. Если в качестве плоской фигуры выбрать треугольник, тогда задача формулируется следующим образом: преобразовать плоскость треугольника общего положения в новой системе плоскостей проекций в плоскость уровня.

Одной заменой плоскостей проекций эту задачу решить невозможно, так как необходимо соблюдать условие: новая плоскость должна быть перпендикулярна незаменяемой. Поэтому решим эту задачу двумя заменами: первой заменой введем плоскость, которая перпендикулярна треугольнику АВС, второй заменой – плоскость, параллельную треугольникуАВС.

Для того, чтобы построить плоскость П₄, перпендикулярную треугольникуАВС,необходимо расположить ее так, чтобы она была перпендикулярна фронтали, либо горизонтали треугольникаАВС.

Пусть П₄перпендикулярна горизонтали, тогда новая осьХ₁₄должна быть перпендикулярнаh₁(рис. 2.17). Построим ее на произвольном расстоянии от треугольникаА₁В₁С₁. Затем из точекА₁,В₁,С₁проведем линии связи перпендикулярно Х₁₄. На каждой из них от осиХ₁₄отложим отрезок, равный расстоянию от фронтальной проекции соответствующей точки до осиХ₁₂. В результате получаем новую проекциюВ₄А₄С₄треугольникаАВС, которая представляет собой прямую, поскольку плоскость треугольникаАВС перпендикулярна плоскости П₄.

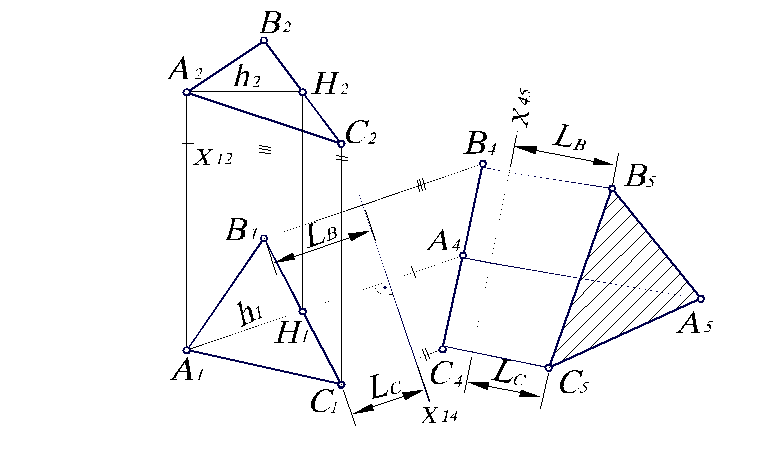
Рис. 2.15. Преобразование плоскости общего положения в плоскость уровня.

Второй заменой вводим вместо П₁плоскость П₅, параллельную плоскости треугольникаАВС. Тогда получается система плоскостей проекций П₄/П₅, осьХ₄₅которой параллельнаВ₄А₄С₄. Она может быть расположена на произвольном расстоянии отВ₄А₄С₄. Далее из точекВ₄ А₄ С₄проводим линии связи перпендикулярноХ₄₅, и на каждой из них от осиХ₄₅откладываем отрезок, равный расстоянию от горизонтальной проекции соответствующей точки до осиХ₁₄. Получим точкиА₅,В₅,С₅, соединив которые имеем треугольникА₅В₅С₅, который и является натуральной величиной треугольникаАВС, поскольку в новой системе плоскостей проекций треугольникАВСпараллелен плоскости П₅.