2.Способы определения усилий в стержнях фермы.

Расчет фермы, как и всякой статически определимой системы начинается с определения опорных реакций, Это делают обычным способом как в балке, составляя уравнения равновесия для фермы в целом. После этого приступают к определению усилий в стержнях.

Основной метод состоит в отделении части фермы и рассмотрения ее равновесия. Этот метод разрезовприменялся и в решении задач сопротивления материалов.

Последовательность действий была определена еще в курсе теоретической механики, когда изучалась статика системы сил на плоскости.

1.Проводят мысленно разрез фермы, который должен проходить, вообще говоря, не более, чем через три стержня, в том числе и через тот, усилие в котором следует определить.

2. Отбрасывают левую или правую часть фермы относительно разреза (удобнее отбрасывать ту часть, к которой приложено большая часть нагрузок).ли вырезается узел, то он просто изывается из фермы.

3. Заменяют действие отброшенной части продольными усилиями в разрезанных стержнях, полагая их все растягивающими ( действующими “от узла”).

4. Составляют уравнение равновесия так, чтобы искомое усилие входило в него как единственное неизвестное.

5. Решают уравнение, находят усилие. Если результат получается со знаком плюс, то стержень растянут, если минус – сжат.

Итак, метод общий – метод разрезов. Но при составлении уравнения равновесия нужно применить такой способ, Который позволяет избежать решения системы совместных уравнений. Различают несколько таких способов: способ моментной точки, способ проекций и способ вырезания узлов.

В строительной механике часто применяют “фирменные” обозначения усилий в стержнях. Буквой О обозначают усилие в элементах верхнего пояса, U– в элементах нижнего пояса,D– в раскосах,V- в стойках. Этим буквам придается два индекса, соответствующих номерам узлов по концам стержня. Некоторые из этих букв оказываются “перегруженными содержанием”. Например, буквойVобозначают вертикальную составляющую опорной реакции и работу внешних сил. Поэтому усилия в стержнях фермы можно обозначать одной буквой (обычноS) с двумя индексами.

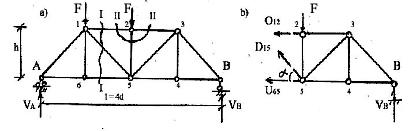
Определим усилия в стержнях фермы, показанной на рис.4.2.

Опорные реакции определим как в балке с пролетом, равным пролету фермы:

-V_B V_B =

Рис.4.2

Найдем усилие O₁₂ .Проведем сечениеI–I(рис.4.2 а).

Отбросим левую часть фермы. и заменим Рис.4.2

ее действие на оставшуюся правую часть неизвестными усилиями О₁₂ ,D₁₅ иU₆₅ , полагая их растягивающими (рис.4.2.b).

Уравнение равновесия нужно составить так , чтобы в него вошло усилие О₁₂ и не вошлиD₁₅ иU₆₅ . Для этого следует взять момент всех сил, приложенных к правой части фермы, относительно точки 5, играющей в данном случае роль моментной точки.

Таким образом, для определения усилия О₁₂примененспособ моментной точки.

За моментную принимают ту точку, в которой пересекаются все неинтересующие нас стержни , попавшие в сечение..Следовательно, в разрез могут попасть иn стержней, если n-1 пересекаются в одной точке. (рис. 4.3).

Найдем усилие в раскосеD₁₅.

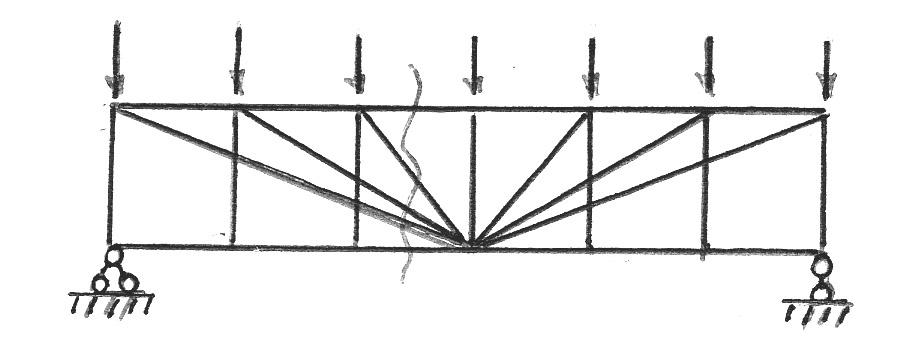
Проводим то же сечение I–I. Изложенный выше способ здесь не применим: моментную точку придется

Рис.4.3

искать на пересечении стержней О₁₂ иU₆₅ , а они параллельны. Поэтому составляем уравнение другого вида: проектируем все силы, приложенные к правой части фермы, на вертикаль, применяяспособ проекций:

Найдем усилие V₂₅.

Провести разрез фермы на две части так, чтобы он прошел через стойку 2-5 и еще через два стержня не удается. Поэтому проводят сечение II–II, применяяспособ вырезания узлов(рис.4.4).

Проектируя все силы на вертикаль, получаем

Рис.4.4

Применяя способ вырезания узлов, нужно помнить, что для системы сходящихся сил можно записать только два уравнения равновесия. Поэтому в вырезаемом узле не должно быть более двух стержней с неизвестными усилиями.

До начала определения усилий в элементах фермы полезно выявить те стержни, усилия в которых при заданной нагрузке равны нулю. Такие стержни называют нулевыми.

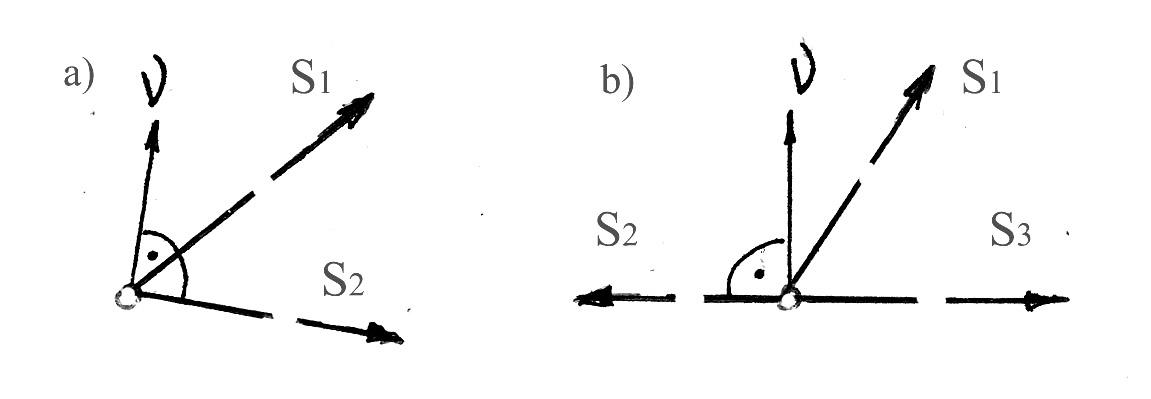
Правила определения нулевых стержней следуют из уравнений равновесия.

Если в узле сходится два стержня и узел не нагружен, то усилия в обоих стержнях равны нулю (рис.4.5a). Проектируя силы на направление, получаем

S₁= 0. После этого из проекции на направлениеS₂Рис.4.5

следует, что и S₂= 0.

Если в узде сходятся три стержня , два из которых лежат на одной прямой и узел не нагружен (рис.4.5b), то усилие в ответвляющемся стержне равно нулю (S₁ = 0), а два других равны между собой (S₂=S₃ ). Первое заключение следует из уравнения равновесия, втрое – получаем, проектируя все силы на прямую, вдоль которой действуют силыS₂ иS₃ .

Пользуясь этими правилами легко установить, что все стержни, перечеркнутые одной чертой в ферме на рис.4.6, нулевые.

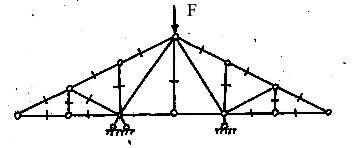
Рис.4.6