5.14. Деревья и их свойства

_{Определение. Деревом называется связный граф, который не содержит замкнутых цепей, т.е. нет цикла, в котором ребра разные.}

_{Свойства дерева:}

_{1. В дереве нет петель и кратных ребер.}

_{Доказательство следует из определения дерева, так как петля и кратные рёбра}

– замкнутые цепи_.

_{2. Любые 2 вершины v и w соединены единственной цепью.}

_{Доказательство следует из определения дерева.}

_{3. Для дерева справедливо следующее соотношение: p = q + 1 (*), где p – число вершин, q – число ребер.}

_{Доказательство (индукцией по p):}

_{а) p = 1 – дерево состоит из одной вершины, q = 0, тогда соотношение (*) выглядит 1 = 1.}

_{б) Пусть соотношение (*) верно для любых деревьев, у которых вершин меньше, чем p.}

_{в) Рассмотрим дерево с p вершинами. Уберем ребро, соединяющее вершины v и w. Наш граф разбился на 2 подграфа и . , – деревья, так как они связны и не имеют замкнутых цепей. Поэтому для них верно индукционное предположение:}

_{VWV W}

_{T1 T2}

_.

_{4. Если любые 2 вершины v и w в дереве соединить ребром, то получим ровно одну замкнутую цепь.}

_{Доказательство следует из свойства 2.}

_{5. Пусть G = (p, q) – дерево, где p > 1. Тогда в дереве G существуют хотя бы 2 вершины v и w такие, что .}

_{Доказательство. Как известно, (по свойству 3). Предположим, что не существуют 2 вершины, степень которых равна 1, т.е. пусть , а у остальных вершин , где . Тогда получаем, что . Пришли к противоречию, значит, существуют вершины v и w такие, что .}

_{Определение. Вершины в дереве, степень которых равна 1, называются концевыми.}

_{Пример дерева:}

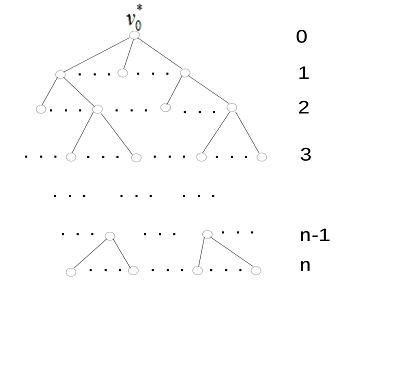
_{где max(n) – глубина (количество ярусов) дерева, – корень дерева (корень – это некоторая выделенная вершина).}

5.15. Деревья и операции над ними

_{Введем три операции:}

_{1. Ребро – дерево с корнем (код 01), дереву из одного ребра дается код 01.}

_{2. Если у нас есть дерево с корнем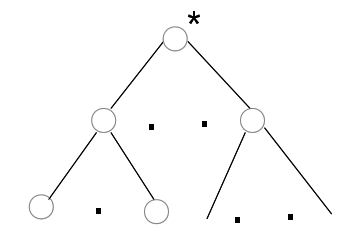, то результат присоединения этого дерева к ребру 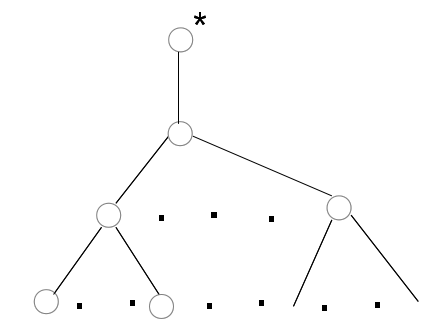– также есть дерево с корнем.}

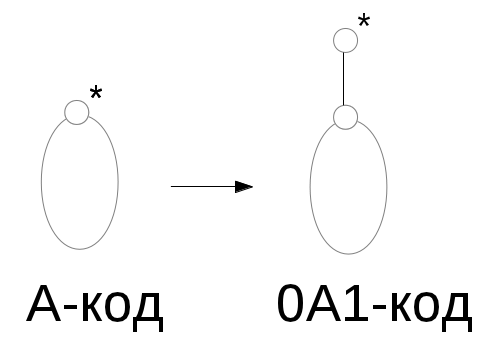
_{При этом пусть дерево с корнем имеет код А, тогда дереву, полученному в результате операции 2, ставится код 0А1.}

_{3. Если у нас есть два дерева с корнем,}

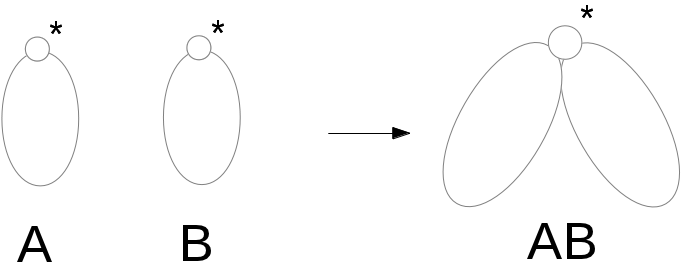
_{то результат склеивания этих деревьев также есть дерево с корнем. Если при этом у одного дерева код А, а у другого код В, тогда у дерева, которое получается склеиванием этих деревьев, код будет АВ.}

_{Замечание. Любое дерево с корнем можно получить при помощи вышеуказанных трех операций, при этом всегда можно определить его код.}

_{Пример. Пусть дано корневое дерево Т, определить его код, где}

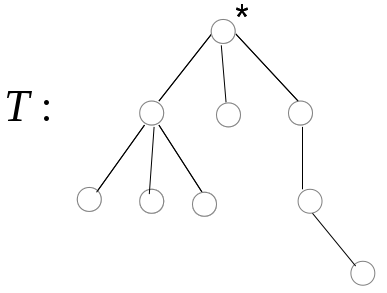
_{Решение: Исходное дерево Т получено из деревьев двукратным применением операции 3, где}

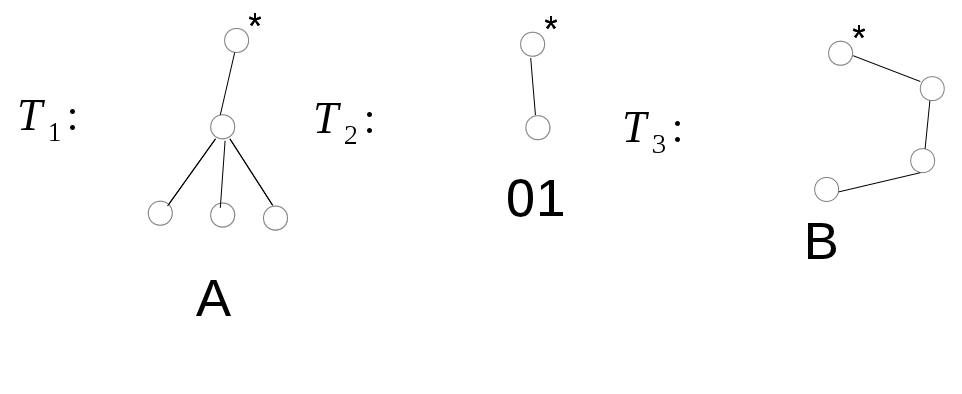
_{тогда код дерева Т – А01В.}

_{1) Дерево получено из дерева с помощью операции 2, где}

_,

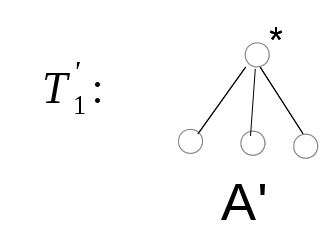_{тогда код дерева А = 0A'1.}

_{Дерево получено из дерева операции 1 двукратным применением}

_{операции 3, тогда код дерева A' = 010101, следовательно, код дерева A = 00101011.}

_{2) Дерево Т2 получено с помощью операции 1, его код – 01.}

_{3) Дерево Т3 получено из дерева операции 1 двукратным применением операции 2, тогда код дерева Т3 В = 000111.}

_{В итоге код корневого дерева Т есть код А01В = 0010101101000111.}

_{Свойства кода дерева:}

_{1) Длина кода дерева равна удвоенному числу его ребер (2q).}

_{2) В любом начальном отрезке (если считать код дерева слева) число нулей числа единиц.}

_{3) Во всем коде число нулей равно числу единиц.}

_{Встает логичный вопрос: как восстанавливать по коду дерево?}

_{Берем произвольный код дерева, где , q – число ребер дерева. Идем слева направо и отмечаем такой момент, когда число нулей совпадает с числом 1. При этом возможны два случая:}

_{1) Пусть равенство наступит в конце кода, тогда , т.е. дерево с кодом получено из дерева с кодом с помощью операции 2.}

_{2) Пусть равенство наступит, не доходя до конца кода, т.е. , а это означает, что дерево с кодом получено из деревьев соответственно с кодами и с помощью операции 3.}

_{Аналогично, т.е. согласно пунктам 1) и 2), восстанавливаем по кодам соответствующие им деревья. Этот процесс называется декодированием. Не сложно доказать (мы практически уже показали), что между деревом и его кодом существует взаимно однозначное соответствие.}

_{Пример. Построить корневое дерево по его коду .}

_{Решение: q = 7. , где . Таким образом, дерево с кодом получено из деревьев соответственно с кодами с трехкратным применением операции 3. Аналогично, дерево с кодом получено из дерева операции 1 с применением операции 2; деревья с кодами и – деревья операции 1; дерево с кодом получено из дерева операции 1 с двукратным применением операции 2. В итоге дерево Т выглядит следующим образом:}