3.10. Единственность представления булевых функций полиномами Жегалкина

Теорема 6. Каждая функция может быть представлена в виде полинома Жегалкина, причем единственным образом.

Доказательство:

1) По следствию 3 теоремы 3

. (4)

Нам необходимо избавиться от отрицаний в сумме (4). Воспользуемся формулой , так как

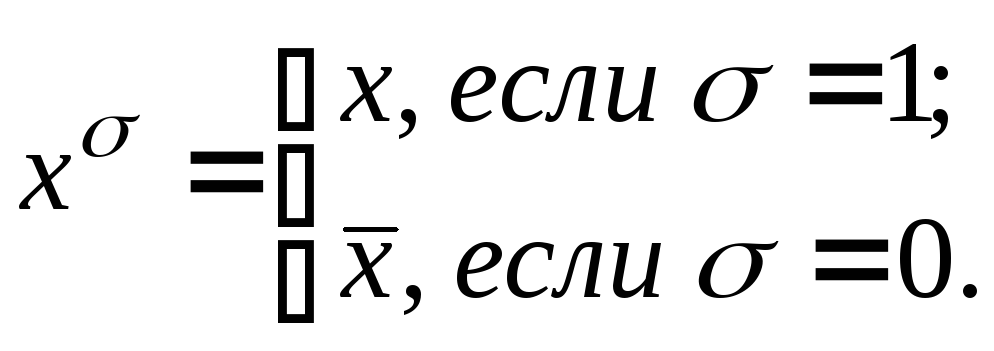
Действительно: если , то , если , то .

Преобразуем формулу (4):

.

В нашей сумме уже нет отрицаний над переменными. Теперь раскроем скобки: ,– различные конъюнкции от переменных. Таким образом, мы показали, что каждая функция изпредставима в виде полинома Жегалкина.

2) Докажем единственность. Для этого подсчитаем число полиномов и сравним с числом функций от n переменных.

Выпишем все различные конъюнкции , каждая коньюнция либо входит в полином, либо не входит, поэтому полиномов всего будет . Число функций ||=.

Вывод:

1) Получили, что число полиномов равно числу функций от переменных.

2) Каждая функция представляется хоть каким-нибудь полиномом.

3) Каждый полином реализует только одну функцию.

Таким образом, представление функции в виде полинома единственно.

Теорема полностью доказана.

3.11. Методы построения полиномов

I. Метод построения с помощью таблицы.

По следствию 3 теоремы 3 функция

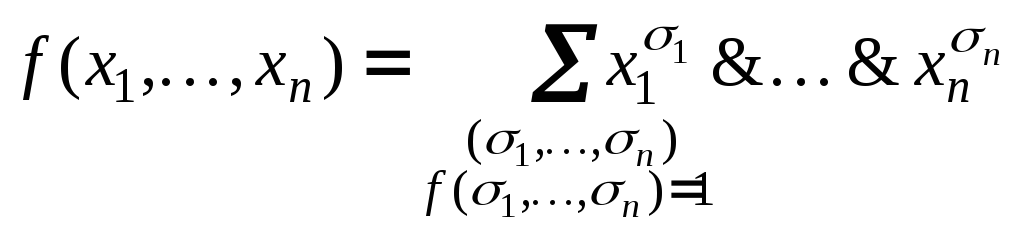(5)

Воспользовавшись формулой x^σ , избавимся от отрицания в сумме (5) и получим полином Жегалкина.

Пример. Выразить xy в виде полинома Жегалкина методом таблиц.

Вначале функцию xy представим в виде таблицы:

	xy
0 0 0 1 1 0 1 1	0 1 (6) 1 1

Далее, согласно (5), =

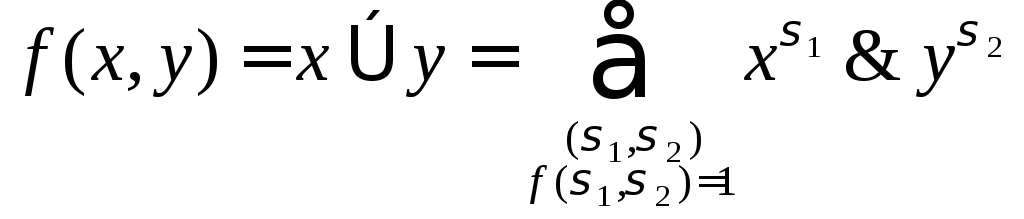, так как , то есть,

мы получили построение дизъюнкции в виде полинома.

II. Метод неопределенных коэффициентов.

Согласно теореме 6 функция

. (7)

_{В сумме (7) неизвестными являются коэффициенты} ,_{их всего} .

Исходя из табличного представления данной функции, точнее, подставив данные каждой строки табличного представления в соотношение (7),

_{получим конкретные значения неизвестных коэффициентов} ._{Далее, подставив значения коэффициентов в соотношение (7), получим полином Жегалкина.}

Пример. Выразить функцию с заданной таблицей (6) в виде полинома Жегалкина методом неопределенных коэффициентов.

_{Согласно (7)} ,_{где неизвестными являются коэффициенты} .

Возьмем наборы:

, тогда

, тогда

, тогда

, тогда

Значит, .

III. Метод суперпозиции.

Зная представление одной функции в виде полинома Жегалкина, всегда можно найти представление в виде полинома других функций, полученных из исходной заменой переменных.

Пример. Известно что . Тогда

1)

2) 3)

.

3.12. Замыкание. Свойства операции замыкания. Замкнутые классы

С понятием полноты тесно связано понятие замыкания и замкнутого класса.

Определение. Пусть – некоторое подмножество функций из.Замыканием называется множество всех булевых функций, представимых в виде формул через функции множества. Замыкание множестваобозначается через.

Отметим некоторые свойства замыкания:

1) ;

2) ;

3) если , то;

4) если мы рассмотрим и,и, то.

Определение. Класс (множество) называетсязамкнутым, если .

Пример:

1) Класс является замкнутым классом.

2) – незамкнутый класс, так как, а

3) – незамкнутый класс, так как подстановкой других переменных мы можем получить из функциифункцию, а.

Замечание. В терминах замыкания и замкнутого класса можно дать другое определение полноты: – полная система, если .