3.6. Совершенная д. Н. Ф., совершенная к. Н. Ф.

Следствие 1. Если в пункте 1 теоремы 3 , то разложение имеет вид:

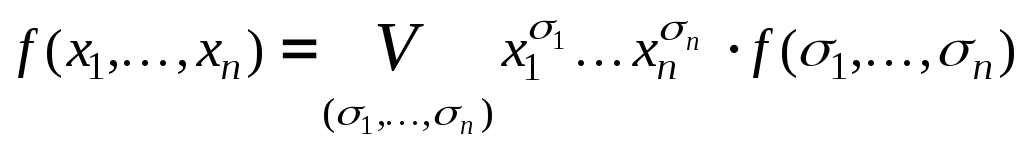. (1)

Если , тогда из (1) следует, что

–Совершенная Дизъюнктивная Нормальная Форма (СДНФ).

Следствие 2. Если в пункте 3 теоремы 3 , то разложение имеет вид:

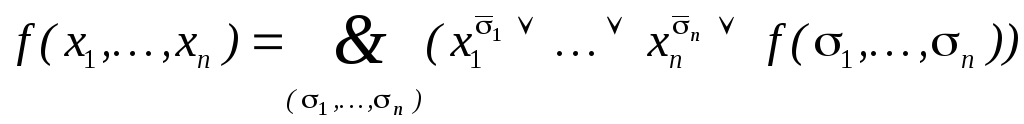. (2)

Если , тогда из (2) следует, что

–Совершенная Конъюнктивная Нормальная Форма (СКНФ).

Следствие 3. Если в пункте 2 теоремы 3 , то разложение имеет вид:

(3)

Если , тогда из (3) следует, что

.

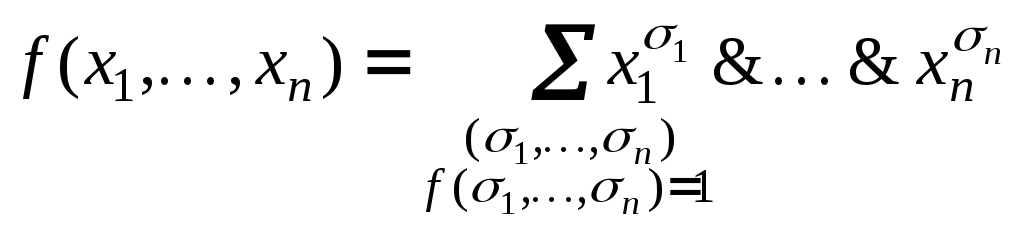3.7. Полные системы

Теорема 4. Каждая булева функция может быть реализована формулой над множеством .

Доказательство: Рассмотрим 2 случая для функции :

1) , тогда мы можем представить по пункту 3 теоремы 2.

2) , тогда из следствия 1 теоремы 3 следует, что .

Определение. Система функций изназываетсяполной в , если любая булева функция может быть записана в виде формулы над этой системой.

Замечание. Из теоремы 4 следует, что система полна в.

Следующая теорема позволяет сводить вопрос о полноте одних систем к вопросу о полноте других систем.

Теорема 5. Пусть даны две системы функций из :

, (I)

, (II)

относительно которых известно, что система I полна в и каждая её функция выражается в виде формулы через функции системыII. Тогда система II является полной в .

Доказательство: Пусть – произвольная функция из. В силу полноты системыI можно выразить формулой над, то есть

.

По условию теоремы:

,

,

Тогда .

То есть мы выразили произвольную функцию в виде формулы над множеством, значит, системаII полна в .

3.8. Примеры полных систем

Следствие 4. Система является полнойв .

Доказательство: –I – система полна в по теореме 4.

–II.

Каждая функция системы I выражается в виде формулы через функции системы II, так как . По теореме 5 системаII полна в .

Следствие 5. Система является полнойв .

Доказательство: Система – I – полнав по следствию 4.

Система – II.

Так как , то по теореме 5 система II полнав .

Следствие 6. Система является полной в.

Доказательство: – I – полнав по следствию 4.

– II.

Так как то по теореме 5 система II полнав .

Следствие 7. Система является полной в.

Доказательство: – I – полнав по следствию 4.

–II.

Так как , то по теореме 5 система II полнав .

3.9. Полиномы Жегалкина

Пусть дан набор из переменных . Надо найти число конъюнкций, не содержащих отрицание, полученных из этих переменных.

Всего их будет 2ⁿ.

Пример:

1) Пусть x₁, x₂, n = 2, тогда: 2) Пусть x₁, x₂, x₃, n = 3, тогда:

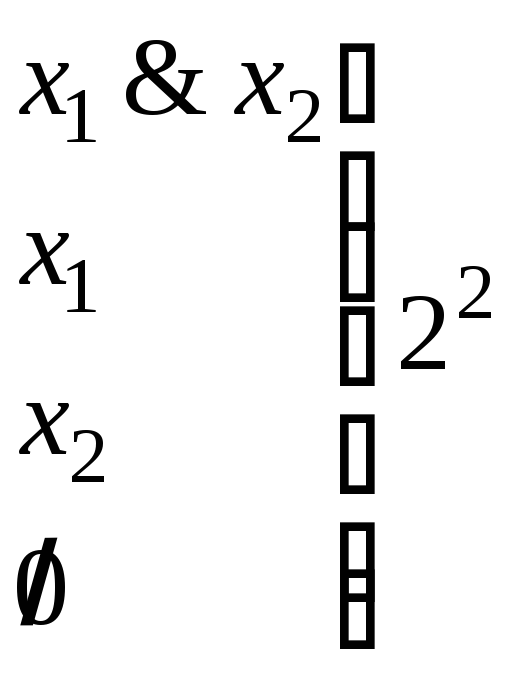
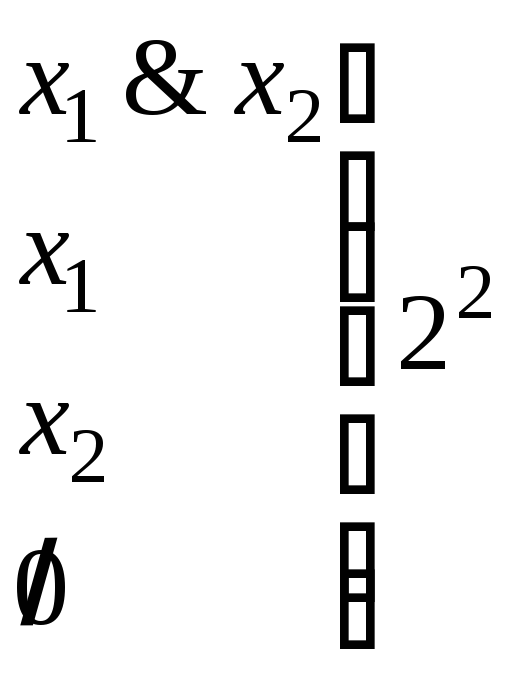
конъюнкций всего

конъюнкций



Пусть – всевозможные конъюнкции, не содержащие отрицания и состоящие из переменных .

Определение. Выражение вида , называется полиномом Жегалкина.