
Дегтярёв Оптимальное управление
.pdf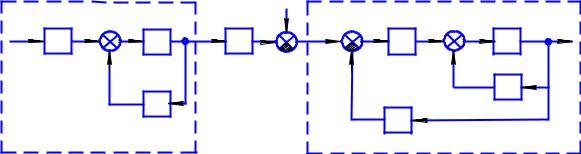
|
|
|
|
|
71 |
|
|
|
алгебраическое. При этом процесс |
ˆ |
|
процесс |
E(t) |
||||
Y (t) и, следовательно, |
||||||||
являются стационарными, так что P(t) P*T const . |
|
|
|
|||||
Запишем уравнения стационарного фильтра Калмана в следующем |
||||||||
виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
v(t) |
|
|
|
w(t) |
|
|
Y(t) |
|
Z(t) |
|
ˆ |
|
|
|
|
|
Y (t) |
|
|||
|
С |
|
N |
|
K |
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
Исходная система |
|
|
|
Фильтр |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Рис. 16 |
|
|
|
|
ˆ |
|
|
|
|
|
|
dY (t) |
ˆ |
ˆ |
ˆ |
|
|
|
|
|
|||||
dt |
AY (t) K0 |
Z (t) N Y (t) , |
Y (t0 ) Y ; |
(5.82) |
||
|
|
|
|
|
|
|
|
K0 PN T R 1 ; |
|
|
|
(5.83) |
|
AP PAT CQC T PN T R 1NP 0 . |
(5.84) |
|||||
Один из часто используемых способов решения уравнения (5.84)
(обычно с помощью ЦВМ) заключается в решении нестационарного уравнения
(5.80) с соответствующими постоянными значениями коэффициентов, из которых составлены матрицы А, С, Q, R, и произвольной неотрицательно определенной матрицей начальных условий для P0 в текущем времени до тех пор, пока полученное решение не достигнет постоянного установившегося значения. Это окончательное значение принимается за искомое решение уравнения (5.84). Такой способ решения удобен тем, что алгоритмы решения дифференциальных уравнений, как правило, эффективнее алгоритмов решения нелинейных алгебраических уравнений.
Замечание 1.

72
Важным свойством полученной ошибки является то, что она
некоррелирована с ошибкой оценивания, [7] т.е.
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
M [Y (t) E(t)] 0 . |
|
|||||
Замечание 2. |
|
|
|
|
|
|
|
|
|
|
||||
Пусть теперь |
уравнение |
измерения имеет вид (5.62), а |
погрешность |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
необходимо |
измерения отсутствует. В этом случае для получения оценки Y (t) |
||||||||||||||
воспользоваться производной (t) наблюдаемого сигнала |
|
|||||||||||||
(t) |
dN(t) |
Y (t) N (t) |
dY(t) |
|
dN(t) |
Y (t) N (t)(A(t)Y (t) C(t)W (t)) , |
||||||||
|
|
|
|
|
|
|||||||||
|
dt |
|
|
|
dt |
|
|
dt |
|
|
||||
которая может быть представлена в виде (5.62) |
|
|||||||||||||
|
|
|
|
|
|
(t) |
|
(t)Y (t) V (t) . |
|
|||||
|
|
|
|
|
N |
|
||||||||
где |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
(t) |
dN(t) |
N (t) A(t), |
V (t) N (t)C(t)W (t) . |
|
|||||||
|
N |
|
||||||||||||
|
|
|
|
|||||||||||
dt
Далее процедура вывода уравнений фильтра совпадает с выше изложенной.
Замечание 3.
Для управляемых систем, описываемых совокупностью уравнений
dY(t) |
A(t)Y (t) B(t)U (t) C(t)W (t), |
Y (0) Y . |
|
||
dt |
0 |
|
|
||
Уравнение фильтра может быть получено аналогично. В этом случае уравнение фильтра будет иметь вид
|
ˆ |
|
|
|
|
|
|
|
|
|
dY |
|
ˆ |
ˆ |
ˆ |
|
|
|
|
|
|
|
|
|
|
||||
|
dt |
A(t)Y (t) K (t) Z (t) N (t)Y (t) B(t)U (t), |
Y (0) |
Y0 |
, |
||||
|
|
|
|
|
|
|
|
|
|
где матрица |
K0 (t) PN T (t)R 1 (t) , |
а корреляционная |
матрица |
||||||
раньше, находится из матричного уравнения |
|
|
|
|
|
||||
(5.85)
P(t) , как и
dP(t) A(t)P(t) P(t) AT (t) C(t)Q(t)CT (t) P(t)N T (t)R 1(t)N (t)P(t) (5.86) dt
73
с начальным условием P(0) P0 .
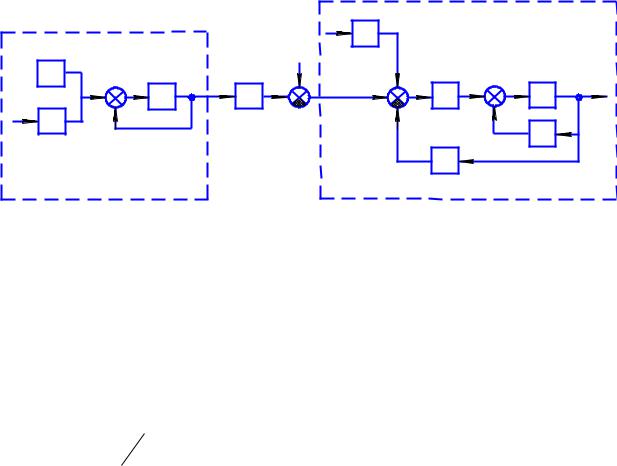
Система оценивания (фильтр) схематически представлена на рис. 17.
u(t)
 B
B
w(t) |
|
|
С |
||
|
Исходная система
|
U(t) B |
|
|
|
|
v(t) |
|
|
|
|
|
|
|
ˆ |
Y(t) N |
Z(t) |
|
|
Y (t) |
K |
|
|||
|
|
|
A |
|
|
|
N |
|
|
|
|
|
Фильтр |
|
Рис. 17
5.5. Синтез локально-оптимального управления линейными стохастическими системами при полной и точной информации.
Пусть управляемое движение в условиях воздействия возмущений описывается системой уравнений
dY(t) |
|
A(t)Y (t) B(t)U (t) C(t)W (t), |
Y (t0 ) Y0 |
(5.87) |
|
dt |
|||
|
|
|
|
Случайный процесс W (t) и начальное состояние Y0 будем считать независимыми, обладающими свойствами (5.28). Предполагается, что состояние Y(t) в любой момент времени t известно. Будем искать управление
U (t) как некоторую линейную функцию текущего состояния |
|
U(t) f (t)Y (t) . |
(5.88) |
Тогда задача определения локально-оптимального управления сводится к |
|
нахождению (r n) -матрицы f (t) . Оптимальную матрицу f0 (t) |
будем искать |
среди матриц, элементами которых являются непрерывные функции со значениями из открытой области.
В качестве функционала, характеризующего управляемое движение,
возьмем математическое ожидание локального функционала J (t) (4.27)
J1(t) M[J (t)].

|
|
|
74 |
|
|
|
|
Введем матрицу корреляционных моментов |
|
|
|
||
|
|
|
P(t) M [Y (t)Y T (t)]. |
|
(5.89) |
|
Используя (5.88), (5.89) функционал можно J1(t) |
преобразовать к виду |
|
||||
|
|
|
t |
|
|
|
J1 |
(t) M Y T (t)G3 (t)Y (t) Y T ( ) f T ( )G2 ( ) f ( )Y ( ) Y T ( )G1 |
( )Y ( )d |
|
|||
|
|
|
t0 |
|
|
|
|
|
|
|
|
(5.90) |
|
|
|
|
|
|
|
|
|
t |
|
|
|
||
|
Sp G3 (t)P(t) |
f T ( )G2 ( ) f ( ) G1( ) P( )d |
|
|
||
|
|
t0 |
|
|
|
|
|
|
|
|
|
|
|
Таким образом, значение критерия качества в текущий момент времени определяется матрицей корреляционных моментов.
Найдем уравнение для ее определения. Уравнение управляемого процесса
(5.87) с учетом (5.88) можно представить в виде
dY(t) dt A(t)Y (t) C(t)W (t),
где матрица
|
|
|
|
|
|
|
|
|
(t) A(t) B(t) f (t) . |
|
|||||||
|
|
|
|
|
|
|
|
A |
(5.91) |
||||||||
B соответствии с (5.54) уравнение для матрицы P(t) будет иметь вид |
|||||||||||||||||
dP(t) |
|
|
|
(t)P(t) [ |
|
(t)P(t)]T C(t)Q(t)CT (t) , |
|
||||||||||
A |
A |
|
|||||||||||||||
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или, с учетом (5.91), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dP(t) |
[ |
|
(t) B(t) f (t)P(t)]P(t) PT (t)[A(t) |
|
|||||||||||||
A |
|
||||||||||||||||
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.92) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B(t) f (t)]T C(t)Q(t)CT (t). |
|
|
|||||||||||||||
Начальным условием является, очевидно, |
|
|
|||||||||||||||
|
|
) M Y Y T Y |
|
|
T P . |
|
|||||||||||
P(t |
0 |
Y |
(5.93) |
||||||||||||||
|
|
0 |
0 |
0 |
0 |
0 |
|
||||||||||
Из (5.92), (5.93) с учетом предположения о симметричности матриц P0 ,
Q(t) непосредственно следует, что матрица P(t) является симметричной, т.е.
P(t) PT (t) .
Таким образом, задача определения оптимального управления свелась к задаче определения матрицы f (t) из условия минимума J1(t) (5.90). Для

75
нахождения ее воспользуемся условием (4.28). Дифференцируя (5.90) и
учитывая (5.92), получим
dJ1(t) dt Sp{[G1(t) dG3 (t) dt f T (t)G2 (t) f (t)]P(t)
G3 (t)[A(t)P(t) PT (t) AT (t) C(t)Q(t)CT (t)
B(t) f (t)P(t) PT (t) f T (t) BT (t)]}.
Выпишем составляющие |
dJ1(t) |
, зависящие от f (t) : |
|
|||||||||||
|
dt |
|
||||||||||||
(t) Sp{ f T (t)G |
2 |
(t) f (t)P(t) G |
(t)[B(t) f (t)]P(t) PT (t) f T (t)BT (t)]}. |
|||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
Обозначим через |
f0 (t) искомую локально-оптимальную матрицу. Введем |
|||||||||||||
в рассмотрение семейство матричных функций сравнения |
|
|
||||||||||||
|
|
|
|
f (t) f0 (t) f (t). |
|
|
|
|||||||
где f (t) - произвольная малая |
вариация матричной |
функции f (t) из |
||||||||||||
рассматриваемого класса. |
|
|
|
|
|
|
|
|
|
|
||||
Приращение (t) , вызванное вариацией матрицы |
f (t) , будет иметь |
|||||||||||||
вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(t) Sp{ f T (t)G |
2 |
(t) f |
0 |
(t)P(t) f T |
(t)G |
2 |
(t) f (t)P(t) |
|
||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|||
G (t)[B(t) f (t)]P(t) PT (t) f T |
(t)BT (t)]} f T (t)G |
2 |
(t) f (t)P(t)} |
|||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.94) |
Учтем далее, что
Sp[ f0T (t)G2 (t) f (t)P(t)] Sp[P(t) f0T (t)G2 (t) f (t)]
Sp[ f T (t)G2 (t) f0 (t)P(t)];
Sp[G3 (t)B(t) f (t)P(t)] Sp[P(t)G3 (t)B(t) f (t)]
Sp[ f T (t)BT (t)G3 (t)P(t)];
Sp[G3 (t)PT (t) f (t)BT (t)] Sp[ f T (t)BT (t)G3 (t)P(t)] .
Тогда из (5.94) следует, что
(t) 2Sp[ f T (t)[G2 (t) f0 (t) BT (t)G3 (t)]P(t)] .
76
В силу произвольности f T (t) и предполагая, что матрица P(t) не особая, из условия (t) 0 получим уравнение для определения оптимальной матрицы f0 (t)
G |
2 |
(t) f |
0 |
(t) BT (t)G (t) 0, |
|
|
|
|
||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
0 |
(t) G 1 |
(t)BT (t)G (t) . |
|
|
(5.95) |
||||||||
|
|
|
|
|
|
2 |
|
3 |
|
|
|
|
||
Найденное значение |
f0 (t) действительно доставляет минимум |
(t) , |
||||||||||||
так как вторая вариация |
|
|
|
|
|
|
|
|
|
|
||||
2 (t) Sp[ f T (t)G |
2 |
(t) f (t) P(t)] |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M [Y T (t) f T (t)G |
2 |
(t) f (t)Y (t)] M [ U T (t)G |
2 |
(t) U T (t)] 0 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
в силу определенной |
|
положительности матрицы |
G2 (t) . |
Здесь |
||||||||||
U(t) f (t)Y(t) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сравнивая (5.88), (5.95) с (4.30), видим, что найденное локально-
оптимальное управление полностью совпадает с локально-оптимальным управлением для детерминированного случая.
Таким образом, синтезированное локально-оптимальное управление для детерминированной системы при полной и точной информации о ее состоянии оказывается локально-оптимальным и для стохастической системы,
возбуждаемой случайным возмущением типа белого шума Аналогичный результат имеет место и при квадратичном критерии
качества (4.19).
Это объясняется тем, что при t t поведение стохастической системы зависит от возмущения W (t) , значение которого предсказать не представляется возможным, и поэтому управление целесообразно оставлять таким же, как в детерминированном случае при отсутствие этих возмущений.
5.6. Синтез локально-оптимального управления линейными стохастическими системами (теорема разделения).

77
Пусть управляемое движение описывается уравнением (5.87), а уравнение измерения – (5.62).
Рассмотрим задачу синтеза, оптимального по критерию
t |
|
|
J1 M Y T ( )G1( )Y ( ) U T ( )G2 ( )U ( ) d Y T (t)G3 (t)Y (t) |
(5.96) |
|
0 |
|
|
При этом будем отыскивать такое управление, значение которого в |
||
момент времени t |
определяется значениями вектор-функции Y ( ) |
на отрезке |
[0, t]. |
|
|
Обозначим |
ˆ |
|
через Y (t) оптимальную оценку состояния управляемой |
||
системы, через E(t) - ошибку оценивания.
Наряду с системой (5.87) рассмотрим соответствующую ей
неуправляемую систему
dX (t) |
A(t) X (t) C(t)W (t), |
X (t0 ) Y (t) |
(5.97) |
|
dt |
||||
|
|
|
с уравнением измерения
p(t) N(t)X (t) V (t).
Для вспомогательной системы задача фильтрации решена и оценка ˆ
X (t)
удовлетворяет уравнению
|
ˆ |
|
|
|
|
dX |
ˆ |
ˆ |
|
|
dt |
A(t) X (t) K0 |
(t)[ p(t) N (t) X (t)] |
(5.98) |
|
|
|
|
|
с начальным условием |
|
|
||
ˆ |
|
X (0) Y0 |
|
где матрица K0 (t) определяется из уравнений (5.79), (5.80). |
|
Из уравнений (5.87) и (5.97) следует, что |
|
t |
|
Y (t) X (t) (t, ) B( )U ( ) d , |
(5.99) |
0 |
|
где (t, ) - фундаментальная матрица решений систем (5.87).
78
Мы отыскиваем управление, которое определяется в момент времени t
значениями вектор-функции Y ( ) на отрезке [0, t]. Тогда для каждой реализации y( ) процесса Y ( ) управление u(t) принимает конкретное
значение, т.е. управление является детерминированным оператором от вектора наблюдений. Поэтому
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
ˆ |
|
|
|
|
|
|
(5.100) |
|
|
|
|
|
|
|
Y (t) X (t) (t, ) B( )U ( ) d |
|
|
|
|||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
Из (5.99) и (5.100) следует, что |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
ˆ |
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
X (t) X (t) Y (t) Y (t) . |
|
|
|
|
|
|
|||
Найдем теперь уравнение для определения |
ˆ |
|
Для этого |
|||||||||||||
Y (t) . |
|
|||||||||||||||
дифференцируя (5.100), получим |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
ˆ |
|
ˆ |
t |
d (t, ) |
|
|
|
|
|
||
|
|
|
dY |
|
dX (t) |
(t,t)B(t)U (t) |
B( )U ( ) d |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
dt |
|
dt |
0 |
dt |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
t |
|
|
|
|
|
|
|
|
|
dX (t) |
B(t)U (t) A(t) |
(t, ) B( )U ( ) d |
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
dt |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dX (t) |
|
|
ˆ |
ˆ |
|
|
|
|
|||
|
|
|
|
|
dt |
B(t)U (t) A(t) Y (t) X (t) . |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Учитывая (5.98), найдем |
|
|
|
|
|
|
|
|||||||||
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dY |
|
|
|
|
|
ˆ |
|
|
|
|
ˆ |
ˆ |
ˆ |
|
|
|
dt |
A(t) X (t) B(t)U (t) K0 |
(t) p(t) N (t) X (t) A(t) Y |
X |
|
(5.101) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
ˆ |
|
|
|
|
|
ˆ |
|
|
|
|
||
A(t)Y (t) |
B(t)U (t) K0 p(t) N (t) X (t) . |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
Далее преобразуем P(t) N (t) X (t) с учетом (5.99), (5.100) |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
ˆ |
ˆ |
|
|
|
|
|
|
|
|
|
P(t) N (t) X (t) N (t)[X (t) X (t)] V (t) |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
ˆ |
|
ˆ |
|
|
|
|
|
|
|
N (t)[Y (t) Y (t)] V (t) Z (t) NY . |
|
|
|
|
||||||||||
Тогда уравнение фильтра окончательно запишется в виде (5.85)
|
ˆ |
|
|
|
|
|
|
|
dY (t) |
ˆ |
|
|
|
|
ˆ |
|
dt |
A(t)Y (t) B(t)U (t) K0 |
(t) Z (t) N (t)Y (t) |
||||
|
|
|
|
|
|
|
|
с начальным условием |
|
|
|
|
|
||
|
|
ˆ |
|
|
|
|
|
|
|
Y0 |
, |
|
|||
|
|
Y (0) |
|
||||
(5.102)
(5.103)
79
т.е. фильтр для определения оценки состояния управления системы есть динамическое звено, на вход которого поступает измеряемый сигнал и управление U (t) .
Теорема разделения. Локально-оптимальное управление системой (5.87)
по критерию (5.96) имеет вид:
|
|
|
|
|
|
1 |
|
|
|
ˆ |
|
|
|
|
|
|
(5.104) |
|
|
|
U (t) G2 |
(t)B(t)G3 (t)Y (t) . |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
- |
Здесь G3 (t), G2 (t) - заданные матрицы локального функционала, а Y (t) |
||||||||||||||||||
решение векторного уравнения (5.102) с начальным условием (5.103). |
|
|
||||||||||||||||
Доказательство. Рассмотрим функционал (5.96). Учитывая, что оценки |
||||||||||||||||||
ˆ |
|
|
|
|
|
|
|
не коррелированны для всех t , функционал (5.96) |
||||||||||
Y (t) и ошибка оценки E(t) |
|
|||||||||||||||||
можно представить в виде |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
(t) |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
J (t) J1 |
(t) J2 |
|
|
|
|
|
|
|
|
||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆT |
(t)G3 |
ˆ |
t |
ˆT |
( )G1 |
ˆ |
U |
T |
(t)G2 |
|
|
|
||||
J1 |
(t) M Y |
|
(t)Y (t) [Y |
( )Y ( ) |
|
( )U ( ) d |
|
|||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
(t)G3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
J1 |
(t) M E |
|
(t)E(t) E( )G1( )E( )d ( ) . |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
Так |
как |
на |
|
J (t) |
не |
|
|
|
ˆ |
|
U (t) , |
то |
задача сводится |
к |
||||
|
|
влияет ни Y (t) , ни |
||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
минимизации |
|
|
при условиях (5.102), |
(5.103). При |
этом оценка |
является |
||||||||||||
J1 |
|
|||||||||||||||||
полностью наблюдаемой. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Рассмотрим выражение |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(t) Z (t) N (t)Y (t) |
|
|
|
|
|
|
|
|
|||||
и найдем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(t, ) M [ (t) T ( )]. |
|
|
|
|
|
|
|
|
|||||
Учитывая, |
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
нетрудно |
|||
что (t) N (t)Y (t) V (t) N (t)Y (t) N (t)E(t) V (t) , |
||||||||||||||||||
показать [7], что
80
(t, ) R(t) (t ) .
Таким образом, в уравнении (5.102) выражение ˆ(t)
Y
)
t
(
N
)
t
(
Z
)
t
(
можно рассматривать как эквивалентный «белый шум» с корреляционной матрицей R(t) (t ) .
В результате мы пришли к задаче синтеза локально-оптимального уравнения в системе (5.102), (5.103), возмущаемой «белым шумом» при полном и точном измерении ее состояния, решение которой было дано в предыдущем разделе. Теорема доказана. Можно показать, что теорема разделения справедлива и при синтезе оптимального управления по квадратичному решению.
