Дегтярёв Оптимальное управление

11

J 0

(1.11)

Для доказательства предположим, что кривая

y(t) доставляет минимум

(максимум) функционалу J [ y(t)]. Это означает,

что при любых y(t)

J 0

( J 0) . Если теперь предположить, что условие (1.11) неверно, то в

силу линейности

J от

y(t) первая вариация J , а значит и J будут менять

знак при смене

знака

y , что противоречит условию J 0

( J 0) и

t1

(t)h(t)dt 0 ,

(1.12)

t0

где h(t) - любая непрерывная функция, то (t) 0 .

Доказательство. Предположим, что условие (t) 0 не выполняется и

существует некоторая точка t* , в

которой (t* ) 0 . Для определенности

Ф h

Ф(t)

положим, что (t* ) 0 . Тогда в силу

h(t)

непрерывности

функции

(t)

существует в

окрестности

точки t*

t0 t

t t t1

Рис. 5

2. В функцию F не входят x и

y .

Тогда

F

F

0 , и уравнение

t

y

Эйлера преобразуется к виду

F( y') c ,

или

y' f (c ) const . В этом случае

y'

1

1

t1

dy

2

J L

1

dt .

t0

dt

Подынтегральная функция

F

1 y'2 не содержит

t

и y ,

а искомая

экстремаль по только что

доказанному представляет

прямую

y c1t c2 ,

проходящую через заданные точки. Постоянные c1 и c2

находятся из системы

уравнений

y

Это отрезок прямой линии. Но какой

экстремум реализует эта прямая остается

h

неизвестно. Необходимы дополнительные

v

исследования.

a

t

Замечание. При

выводе

уравнения

Рис. 7

Эйлера предполагали,

что y(t)

- скалярная

функция. В том случае, когда

y(t) - есть

векторная функция размерности n , подынтегральная

функция

имеет вид

F F (t, y1,... yn , y1',... yn ') ,

а граничные точки A и B задаются в (n 1) - мерном

пространстве yi (t0 ) yi0 , yi (t1) yi1 . В этом случае

t1

n

F

n

F

J

yi

yi d t .

yi

t0

i 1

yi

i 1

Используя необходимое условие экстремума J 0,

и основную лемму

вариационного исчисления, получим систему n уравнений второго порядка

F

d

F

0

i 1,....... n.

(1.19)

yi

d t

yi

t1

I F (t, y, y', y'') dt ,

t0

y(t0 ) y0 ;

;

y(t1) y1;

y'(t0 ) y0

y'(t1) y1 .

19

Поскольку искомая экстремаль при нефиксированных граничных точках

должна быть экстремалью и среди кривых сравнения, имеющих с нею общие

граничные точки, она должна удовлетворять уравнению Эйлера и должно

выполняться уравнение.

F

d F 0

(1.21)

y

dt y'

Тогда из (1.20) следует, что

J

F

y(t1)

F

y(t0 )

t0

(1.22)

F (t, y, y )

t1 F (t, y, y )

t0

y t

y t

t1

0

1

В выражение (1.22),

кроме независимых вариаций t0 , t1

входят, так

называемые

изохронные

вариации

y(t1), y(t0 ) ,

которые

не

являются

независимыми. Выразим изохронные вариации через приращения конечных

значений y0

и y1 . Поскольку эта зависимость нелинейная, то линеаризируя

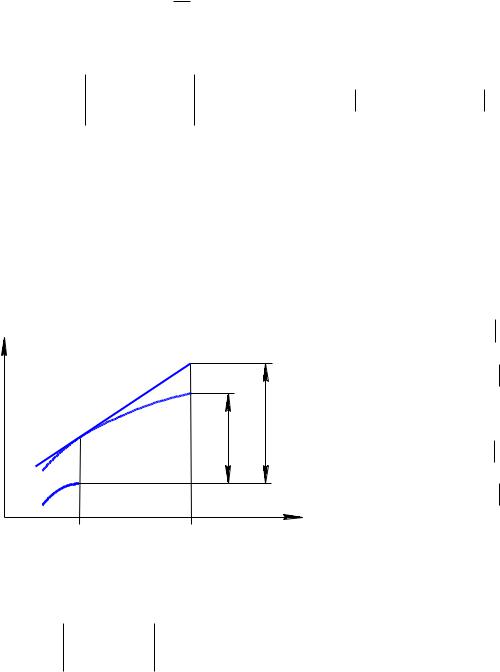
ее, получим (рис. 8).

y(t)

y1

y(t1) y

t1

t1,

y0

y(t0 ) y

t

t0 ,

0

y1

или

y1

y(t1) y1 y t1

t1,

y(t1 )

y(t0 ) y0 y

t

t0 .

0

t1

t1 t1

t

Используя

полученные

Рис. 8

соотношения, найдем

из

(1.22) и

(1.11)

J

F

y1

F

F

y t

y t

y0 F (t, y, y ) y

y

t1

0

t

1

1

(1.23)

F

t0 0.

F (t, y, y ) y

y t

0

1. Точки A и B заданы. В этом случае

t0 t1 y0 y1 0 , условие

(1.23) выполняется тождественно и дополнительной информации не дает.

2. Координаты t0 и t1 , заданы, а

y0

и

y1 произвольны. В этом случае

t0 t1 0 и из

условия

трансверсальности получаем

дополнительно два

условия для определения y0

и y1

F

0

F

0

y

y

t

0

t

1

3. Точка A

задана,

а координаты

точки

B связаны

зависимостью

f (t1, y1) 0 . В этом случае

t0 , y0 0 ,

а

вариации

t1 и

y1 связаны

зависимостью

f

f

f

t

t

y 0

y

1

t

,

t1

1

y1

1

1

1

f

y

1

и из условия трансверсальности получим недостающее условие

f '

t1

F (t,y,y') y' F

F

0 .

y'

t

y'

f ' y

1

1

t1

F

d

F

0,

i 1, 2,..., n

(1.24)

yi

dt yi