
Дегтярёв Оптимальное управление
.pdf51
Пусть теперь рассматривается управляемое движение на отрезке t [0.T ] ,
где T - некоторый фиксированный момент времени. Потребуем также, чтобы в
момент времени T матричная функция G3 (t) |
удовлетворяла конечному |
условию |
|
G3 (T ) G3 |
(4.34) |
Тогда из сравнения формул (4.24), (4.26), (4.22) и (4.30), (4.33), (4.34)
следует, что локально-оптимальное управление(4.30) по критерию (4.27) с
матрицей G3 (t) , определяемой из уравнения (4.33) с условием (4.34) совпадает с управлением (4.24), оптимальным по квадратичному критерию (4.19) на интервале t [0.T ] .
5. Оптимальное управление стохастическими системами в условиях неопределенности.
5.1. Характеристики случайных сигналов В пособие в качестве математических моделей возмущающих
воздействий и погрешностей измерений используются стохастические
(случайные) процессы и последовательности.
Случайный процесс Y(t) - это такая функция, значение которой в фиксированный момент t есть случайная величина, т.е. случайный процесс можно рассматривать как случайную величину, зависящую от параметра t . В
том случае, когда параметр t меняется дискретно, случайный процесс называют случайной последовательностью.
Через y(t) будем обозначать реализацию случайного процесса Y(t) .
Следует отметить, что многие статистические характеристики случайных процессов и последовательностей совпадают.
Как известно, наиболее полной характеристикой случайного процесса является n - мерный закон распределения
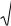
|
|
52 |
|
|
|
|
|
|
|
|
|
|
|
Fn ( y1, y2 , ..., yn , t1,t2 , ...,tn ) P(Y (t1) y1, Y (t2 ) y2 ,..., Y (tn ) yn ) |
( 5 . 1 ) |
||||||||||||
или n -мерная плотность распределения |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
n F ( y , y |
2 |
,..., y |
n |
,t ,t |
2 |
,..., t |
n |
) |
|
||
fn ( y1 |
, y2 ,..., yn , t1, t2 , ..., tn ) |
n |
1 |
|
|
1 |
|
|
(5.2) |
||||
|
y1, y2 ,..., yn |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||
Здесь символом P обозначается вероятность события, |
заключенного в скобках. |
||||||||||||
Значение n |
может быть любым от I |
до |
. Для произвольного |
случайного |
|||||||||
процесса такую информацию иметь невозможно. Однако существует класс случайных процессов (последовательностей), называемых марковскими, для которых статистические характеристики полностью определяются двумерным
законом распределения или двумерной плотностью распределения. |
||
Часто, |
особенно в прикладных задачах, для статистического описания |
|
случайных |
процессов используют начальные M [Y k (t)] |
и центральные |
M [Y (t) M [Y (t)])] k моменты k -гo порядка. Здесь символом |
M обозначена |
|
операция осреднения (математического ожидания). Наиболее важную роль
играют следующие моменты: |
|
|
|
|
|
|
|
|
|||||||||
|
- |
математическое ожидание (среднее значение) |
|
|
|
||||||||||||
|
|
|
|
|
|
my (t) M [Y (t)] ; |
|
|
|
|
(5.3) |
||||||
|
- |
дисперсия случайного процесса |
|
|
|
|
|
||||||||||
|
|
|
|
D |
y |
(t) M[(Y (t) m |
y |
(t))2 |
] ; |
|
|
|
(5.4) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
- |
второй начальный момент |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
(t) M [Y 2 |
(t)] M [(m |
y |
(t) Y (t))2 |
] m2 (t) D |
y |
(t) , |
(5.5) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
Y (t) Y (t) my (t) |
- |
центрированный |
случайный |
|
процесс с |
нулевым |
||||||||||
математическим ожиданием; |
|
|
|
|
|
|
|
|
|||||||||
|
- среднеквадратичное отклонение |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
y (t) Dy (t) . |
|
|
|
|
(5.6) |
||||||
Из |
определения my (t) , |
Dy (t) , y (t) |
и y (t) следует, что эти |
величины |
|||||||||||||
характеризуют случайный процесс только в фиксированном сечении t . Для
53
характеристики связи двух различных сечений случайного процесса используется корреляционная функция;
K y (t1,t2 ) M [Y (t1)Y (t2 )]. |
|
|
|
(5.7) |
||||||||||||
Если математическое ожидание my (t) |
случайного процесса не зависит от |
|||||||||||||||
времени, а корреляционная функция |
является |
функцией одного аргумента |
||||||||||||||
t2 t1 , то такой процесс называется стационарным в широком смысле. |
||||||||||||||||
Если плотность |
распределения fn ( y1, ..., yn , t1, ..., tn ) имеет |
гауссовский |
||||||||||||||
характер, то такой процесс называют гауссовским |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
( y m y ) 2 |
|
|
|
|
||
|
1 |
|
|
|
|
|
2D y |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
f ( y) |
|
|
|
|
e |
|
|
. |
|
|
|
|
||||
y |
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
||||||||||
Гауссовский |
процесс |
|
|
полностью |
определяется |
заданием |
||||||||||
математического ожидания my (t) |
и корреляционной функции K y (t1,t2 ) . |
|||||||||||||||
Важной характеристикой стационарного случайного процесса в широком |
||||||||||||||||
смысле является спектральная плотность |
S y ( ) |
- плотность распределения |
||||||||||||||
дисперсии (энергии) по частотам. |
|
|
|
|
|
|
|
|
||||||||
Спектральная |
плотность |
S y ( ) |
и |
корреляционная функция |
K y ( ) |
|||||||||||
связаны прямым и обратным преобразованием Фурье: |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K y ( ) S y ( )e j d ; |
|
|
|
(5.8) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
S y |
( ) |
|
K y ( )e j d . |
|
|
(5.9) |
||||||||||
2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Чисто случайный процесс (последовательность) - это процесс, для которого случайные величины Y (t1), Y (t2 ), ... взаимно независимы при любых значениях аргументов. Такой процесс полностью характеризуется одномерной функцией распределения. Чисто случайный стационарный процесс называют белым шумом, если корреляционная функция имеет вид - функции.
Спектральная плотность такого процесса постоянна по всем частотам. Так как
54
Dy K y (0) , то нетрудно видеть, что дисперсия белого шума является
бесконечно большой. Такие процессы в природе реально не существуют.
Однако реальный шум по его воздействию на систему может быть заменен белым шумом. Кроме того, реальный случайный процесс можно представить как выходной сигнал некоторой системы (формирующего фильтра), на вход которой поступает белый шум. Поэтому задача статистического анализа или синтеза систем с реальными характеристиками случайных воздействий может быть сведена к задаче статистического анализа или синтеза, когда входным сигналом является белый шум. В настоящем учебном пособии, как правило,
будут использоваться модели белых шумов и чисто случайных последовательностей.
Наряду со скалярными случайными процессами можно рассматривать и
векторные случайные процессы:
Y (t) (Y1(t),Y2 (t), ...,Yn (t)), |
(5.10) |
где каждая компонента Yi (t) является случайным процессом. Для характеристики векторного случайного процесса вводятся следующие векторы
иматрицы:
-математическое ожидание my :
|
|
|
my (t) M [Y (t)]; |
|
|
|
(5.11) |
|||
- дисперсионная матрица Py (t) : |
|
|
|
|
|
|||||
|
|
|
|
|
T |
|
|
|
|
|
|
|
Py (t) M[Y (t)Y |
(t)] |
|
|
(5.12) |
||||
с элементами |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pyij (t) M [Y i (t)Y j (t)]; |
|
(5.13) |
|||||||
- ковариационная матрица K y (t1,t2 ) : |
|
|
|
|
||||||
|
|
|
|
|
T |
|
|
|
|
|
K |
y |
(t ,t |
2 |
) M Y (t )Y |
(t |
2 |
) |
(5.14) |
||
|
1 |
|
1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
с элементами
55
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K yij (t1,t2 ) M [Y i (t1)Y j (t2 )] ; |
|
|
(5.15) |
||||||||||||||||||
- матрица |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
(t ,t |
2 |
) M[Y (t )Y T (t |
2 |
)] |
|
|
|
|
(5.16) |
||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
с элементами |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yij |
M[Yi (t1)Y j (t2 )] . |
|
|
|
|
|
|
(5.17) |
||||||||||||
|
|
|
|
|
|
|
|
|
)T означает транспонирование. |
|
|||||||||||||
Здесь Y (t) Y (t) m |
j |
(t), ( |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Непосредственно |
из |
определения |
матрицы |
Py (t) видно, что на ее |
|||||||||||||||||||
диагонали расположены дисперсии составляющих случайного процесса. |
|
||||||||||||||||||||||
Матрицы Py (t) , |
K y (t1,t2 ) |
и y (t1,t2 ) |
обладают следующими свойствами: |
||||||||||||||||||||
|
|
|
|
|
|
|
|
Py (t) K y (t,t) ; |
|
|
|
|
|
|
(5.18) |
||||||||
K |
y |
(t ,t |
2 |
) K T |
(t |
2 |
,t ) |
|
|
для всех t |
и t |
2 |
(5.I9) |
||||||||||
|
1 |
|
|
|
y |
|
|
1 |
|
|
|
|
|
|
1 |
|
|
||||||
|
y |
(t ,t |
2 |
) K |
y |
(t ,t |
2 |
) m |
y |
(t ) mT (t |
2 |
). |
|
|
(5.20) |
||||||||
|
1 |
|
|
|
|
1 |
|
|
|
1 |
|
y |
|
|
|
|
|||||||
Для стационарного |
|
векторного |
случайного |
процесса Y(t) |
вводится |
||||||||||||||||||
матрица спектральных плотностей как преобразование Фурье ко вариационной матрицы K y (t2 t1) , т.е.
|
1 |
|
|
S y ( ) |
K y ( )e j d . |
||
|
|||
|
2 |
||
|
|
|
|
Матрица S y ( ) обладает следующим свойством:
S y ( ) STy ( )
5.2. Математическое описание линейных систем при случайных возмущениях.
(5.21)
(5.22)
В общем виде уравнение управляемой динамической системы может быть записано в виде:
Y (t) Lt [Y0 ,U (t),W (t)], |
(5.23) |
56
где Lt - оператор (или в частном случае функция) системы, т.е. совокупность правил, по которым преобразуются начальное условие Y0 Y (t0 ) , управляющие воздействия U (t ), t [t0 , t], возмущающие воздействия W (t ), t [t0 , t] в выход системы Y (t) в момент t .
Если параметр t меняется непрерывно, то такую систему будем называть непрерывной; если t меняется дискретно, то система называется дискретной.
Если оператор L не зависит от параметров t и Y0 , то такую систему называют стационарной. Оператор L может быть линейным или нелинейным,
однородным или неоднородным и может задаваться в различной форме,
например, в форме дифференциальных и интегродифференциальных уравнений, с помощью передаточных функций и разностных уравнений.
В данном учебном пособии будут рассматриваться только линейные
системы.
Рассмотрим системы, описываемые дифференциальными уравнениями.
Обозначим через Y (t) n -мерный вектор состояния системы; через
U(t) - -мерный вектор управляющих воздействий; через W (t) - q -мерный
вектор возмущений. Тогда уравнение движения линейной непрерывной динамической системы можно записать в следующей дифференциальной форме:
|
dY(t) |
A(t)Y (t) B(t)U (t) C(t)W )(t), Y |
Y (t |
|
) . |
(5.24) |
|
|
|
0 |
|||||
|
dt |
0 |
|
|
|
||
|
|
|
|
|
|
||
Здесь A(t) , B(t) , C(t) - матрицы размерностей n n, |
|
n , n q соответственно. |
|||||
Элементами этих матриц являются непрерывные функции. Если матрицы A, B
и C являются постоянными, то управляемая система называется стационарной.
Уравнения (5.24) обычно называют уравнениями состояния, так как они описывают изменение переменных состояния системы во времени.
Для целей управления необходимо знать состояние системы в любой текущий момент времени. Однако с помощью измерителей можно получить информацию, как правило, только о некоторых составляющих процессах или их комбинациях. Кроме того, наблюдаемые (выходные) переменные могут
57
содержать погрешности измерения. В дальнейшем будем предполагать, что уравнения измерений имеют вид:
|
Z(t) N(t)Y (t) V (t) , |
|
(5.25) |
где Z(t) - |
m -мерный наблюдаемый сигнал; N(t) |
- матрица размерности |
|
(m n) , характеризующая способ измерения; V (t) |
- |
погрешность измерения. |
|
Если N(t) E |
( E - единичная матрица) и V 0 , |
то говорят, что измерение |
|
полное и точное.
В некоторых случаях удобно представить решение системы (5.24) в
интегральной форме через фундаментальную матрицу решений (t, ) , которая удовлетворяет следующему матричному уравнению:
d (t, ) |
A(t) (t, ), |
( , ) I |
( 5 . 26 ) |
|
dt |
||||
|
|
|
В интегральной форме решение системы (5.24), в соответствии с формулой Коши, можно представить в следующем виде:
|
t |
|
|
Y (t) (t,t0 )Y0 (t, )[B( )U ( ) C( )W ( )]d |
|
||
|
t0 |
(5.27) |
|
t |
t |
||
|
|||
(t,t0 )Y0 (t, ) B( )U ( ) d (t, )C( )W ( ) d . |
|
||
t0 |
t0 |
|
|
В выражении (5.27) первая составляющая учитывает свободное движение,
обусловленное начальным условием Y0 , вторая составляющая учитывает вынужденное движение, обусловленное управляющими воздействиями на интервале времени [t0 , t] , третья составляющая характеризует вынужденное движение, обусловленное возмущениями W на интервале [t0 , t] .
Относительно системы (5.24), (5.25) сделаем следующие предположения:
1)матрицы A(t), B(t), C(t), N(t) не являются случайными;
2)случайные процессы W (t) и V (t) и случайное начальное состояние системы Y0 не коррелированы между собой и имеют следующие статистические характеристики:

|
|
58 |
|
|
|
M Y0 Y0 ; |
|
T |
|
|
|
M Y 0 |
Y 0 P0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M W (t) 0; |
M W (t) W T ( ) Q(t) (t ); |
(5.28) |
|||
M V (t) 0; |
M V (t) V T ( ) R(t) (t ); |
|
|
||
M V (t) Y T 0; M W (t)Y T 0; |
M V (t) W T |
( ) 0. |
|
||
0 |
|
0 |
|
|
|
Из соотношений (5.28) видно, что случайные процессы W (t) и V (t) являются процессами типа белого шума. Матрицы Q(t), R(t), P0 и вектор Y0 считаются известными. Предполагаются известными в каждый момент времени t и
управляющие воздействия.
Одним из видов динамических систем являются дискретные системы,
которые можно разделить на два типа:
а) собственно дискретные системы, такие как ЦВМ, автоматы различных
типов и т.д.;
б) дискретные системы, которые получаются в результате использования непрерывных систем в дискретные моменты времени, в частности, при использовании в контуре управления вычислительных машин. Поведение дискретных систем обычно описывают разностными уравнениями, которые
являются аналогом дифференциальных уравнений для непрерывных систем.
|
|
|
Рассмотрим поведение |
непрерывной |
U |
|
|
системы с дискретным управлением, |
|
|
|
|
||
|
|
|
которое можно представить в виде кусочно- |
|
|
|
|
постоянной вектор-функции |
(рис. 15), т.е. |
|
|
t |
управляющие воздействия можно записать в |
|
t0 |
t1 t2 t3 t4 |
t5 |
следующем виде: |
|
|
|
|
|
|
|
Рис. 15 |
|
|
|
|
|
|
u(t) u(ti ) |
для |
ti t ti 1, i 0,1,2,..., |
|
|
(5.29) |
|
где ti |
- последовательность моментов времени, не обязательно равноотстоящих |
|||
друг от друга. |
|
|
|
|
59
Если нас интересует состояние системы только в дискретные моменты времени tk , то непрерывную систему (5.24) в эти моменты, используя соотношение (5.27), можно записать в следующем виде:
|
tk 1 |
|
Y (tk 1 ) (tk 1,tk )Y (tk ) |
(tk 1, ) B( )u( ) d |
|
|
tk |
(5.30) |
|
tk 1 |
|
|
|
|
|
(tk 1, )C( )W ( ) d . |
|
|
tk |
|
Учитывая (5.29), соотношение (5.30) перепишем в виде: |
||
|
tk 1 |
|
Y (tk 1 ) (tk 1,tk )Y (tk ) |
(tk 1, ) B( ) d u(tk ) |
|
|
tk |
(5.31) |
|
tk 1 |
|
|
|
|
|
(tk 1, )C( )W ( ) d . |
|
tk
Третье слагаемое в соотношении (5.3I) можно рассматривать как некоторую случайную последовательность. В том случае, когда случайный процесс типа белого шума, то справедливо следующее соотношение:
tk 1 |
|
|
|
|
(tk 1, )C( )W ( ) d C(k 1, k)Wk , |
|
|
||
tk |
|
|
|
|
где Wk - чисто случайная последовательность. |
|
|
|
|
Вводя обозначения |
|
|
|
|
Yk Y (tk ); |
A(k 1, k) (tk 1,tk ); |
uk u(tk ); |
|
|
|
tk 1 |
|
|
(5.32) |
B(k 1, k) |
(tk 1, ) B( ) d , |
|
|
|
|
tk |
|
|
|
систему уравнений (5.31) запишем в виде: |
|
|
|
|
Yk 1 A(k 1,k)Yk B(k 1,k)uk C(k 1,k)Wk , |
k 0,1,2,... |
(5.33) |
||
Матрицы A(k 1,k), B(k 1,k), C(k 1,k) называются переходными матрицами по состоянию, управлению и возмущению соответственно; k 0,1,2,... -
дискретное время.
Уравнение измерений, соответственно, можно записать в виде:

60 |
|
Zk 1 N(k 1)Yk 1 Vk 1 . |
(5.34) |
Иногда систему (5.33) - (5.34) записывают в следующем виде: |
|
Yk A(k, k 1)Yk 1 B(k, k 1)uk 1 C(k, k 1)Wk 1 , |
(5.35) |
Zk N(k)Yk Vk , k 1,2,... . |
(5.36) |
Относительно систем (5.33), (5,34) будем предполагать, что:
1) матрицы A(k 1, k), B(k 1, k), C(k 1, k), N(k) являются неслучайными;
2) случайные последовательности Wk , Vk являются чисто случайными и некоррелированными между собой, а также некоррелированными со случайным начальным условием Y0 , т.е.:
M Y |
Y |
; |
M (Y Y )(Y Y |
)T P ; |
||||||||||
0 |
|
0 |
|
0 |
|
0 |
0 |
|
0 |
0 |
||||
M W |
|
0; |
M |
W W T |
Q |
kj |
; |
|
||||||
k |
|
|
|
|
k |
|
j |
|
k |
|
|
|
||
M V |
0; |
|
V V T R |
|
|
|
(5.37) |
|||||||
M |
kj |
; |
|
|
||||||||||
k |
|
|
|
|
k |
j |
|
|
k |
|
|
|
||
M Y V T 0; |
M Y W T |
0, |
M V W T 0. |
|||||||||||
0 |
|
k |
|
0 |
|
k |
|
|
|
|
k |
j |
||
Пример. Рассмотрим вращательное движение тела вокруг одной из осей |
||||||||||||||
под действием возмущающего момента M B . Уравнения движения имеют вид: |
||||||||||||||
|
|
|
J |
d 2 |
M |
|
, |
|
|
|
|
|
(5.38) |
|
|
|
|
|
B |
|
|
|
|
|
|||||
|
|
|
|
d t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где J - момент инерция тела; - угол поворота тела в некоторой инерциальной системе координат. Вводя новые переменные
Y (t) (t), |
Y (t) |
d |
, W M |
|
, |
(5.39) |
|
B |
|||||
1 |
2 |
d t |
|
|
|
|
|
|
|
|
|
|
получим уравнения движения объекта в нормальной форме:
dY |
AY CW , |
A |
|
0 |
1 |
|
, C |
0 |
. |
(5.40) |
|
|
|||||||||
|
|
1 |
||||||||
d t |
|
0 |
0 |
|||||||
|
|
|
|
|
J |
|
|
|||
|
|
|
|
|
|
|
|
|
|
Для этой системы уравнений фундаментальная матрица (t, ) состоит из двух вектор-столбцов решений следующей системы уравнений
