Дегтярёв Оптимальное управление

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский национальный исследовательский технический университет им. А. Н. Туполева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

На экстремали I 0, тогда I 2 I

.pdf

Скачиваний:

Добавлен:

22.03.2016

Размер:

1.68 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 83 4 5 6 7 8 > Следующая >>>

y'i

yi1

y'i

i 1

y'i t

i 1

(1.25)

F y'i

yi0

y'i

i 1

Из условия трансверсальности можно получить систему соотношений для определения граничных значений (2n 2) параметров (t0 , t1, y10 , y20 ,..., yn0 , y11, y21,..., yn1) . В общем случае эти параметры могут быть связаны условиями

fk (t0 ,t1, y10 ,..., yn1) 0

k 1,2,...m

m 2n 2 ,

(1.26)

тогда соответствующая система уравнений в вариациях будет иметь вид:

f k

yi0

f k

yi1 0

k 1,2,...m.

(1.27)

i 1

Используя полученную систему линейных алгебраических уравнений

(1.27),

можно выразить

зависимых переменных через [2n 2 m]

независимых переменных и из условия трансверсальности (1.25) получить

[2n 2 m] уравнений, которые совместно с (1.26) дают замкнутую систему уравнений для определения (2n 2) переменных (координат граничных точек).

2.7. Вариационные задачи на условный экстремум.

До сих пор мы рассматривали задачи поиска функций из заданного

	t1
класса, доставляющих экстремум функционалу
	J F (t, y, y ) d t . При этом
	t0

рассматривались случаи фиксированных или нефиксированных граничных условий. Других ограничений на выбор функций сравнения не было. Однако,

при решении прикладных задач при принятии того или иного решения, в том числе оптимального, всегда приходится учитывать совокупность ограничений по энергопотреблению, быстродействию, точности, (текущей или конечной),

надежности и т.п. Эти ограничения всегда будут накладывать ограничения на выбор допустимых вариаций. Поиск экстремума функционала при наличии дополнительных ограничений (связей), называется задачей на условный экстремум.

Обычно различают связи трех типов:

а) голономные связи – связи, не содержащие производных искомых функций

k (t, yi (t)) 0, i 1, 2,..., n; k 1, 2,..., m; m n ;

б) неголономные связи – связи, содержащие производные искомых функций

k (t, yi (t), y'i (t)) 0, i 1,2,..., n; k 1,2,..., m; m n ;

в) изопериметрические (интегральные связи)

J k [ yi (t), y'i (t)] ck ,

k 1, 2,..., m;

m n;

ck const .

Вариационные задачи на условный экстремум при голономных и неголономных связях можно (теоретически) решить методом исключения зависимых переменных. Тогда задача на условный экстремум сводится к задаче на безусловный. Однако такой подход практически неприменим ввиду сложности процедур исключения зависимых переменных. Поэтому наибольшее распространение получил метод множителей Лагранжа. Рассмотрим применение этого метода в задаче минимизации функционала

t1
J F (t, y(t), y'(t)) d t					(1.28)
t0
при наличии связей
k (t, y(t)) 0,	k 1, 2,..., m;			m n,	(1.29)
граничные условия будем считать заданными.
В соответствие с методом Лагранжа вводится вспомогательный
функционал
t1				m
J * H (t, y(t), y'(t)) d t,		H	F	k k ,	(1.30)

t0	k 1

					m
где k (t)	- неопределенные пока множители Лагранжа. На связях k k 0 и
					k 1
Н F и	функционалы J *	и	J	ведут себя одинаково, т.е.	экстремум J *
достигается одновременно		с	J	при условии, что y(t)	удовлетворяют

уравнениям связей (1.29), независимо от (t) .При заданных граничных условиях, как и ранее, получим

t1	n	H	d	H
J *					yi d t .
		yi
t0	i 1		dt y'i

Однако в этом случае нельзя воспользоваться основной леммой вариационного исчисления, так как yi - не является независимыми.

Воспользуемся свободой выбора множителей Лагранжа и выберем k (t) таким образом, чтобы выполнялись m уравнений

H	d	H
			0,	i 1, 2,..., m ,

yi		yi
	dt

тогда

J *

d t .

i m 1

dt yi

В последнем выражении yi

уже

независимы и,

воспользовавшись

основной леммой вариационного исчисления, получим:

i m 1,..., n .

dt y'i

Таким образом, для определения

n+m функций

yi (t) и k (t) мы

получили систему m и n уравнений

i 1, 2, ..., n

y'i

dt y'i

(1.31)

0 k (t, y(t)) 0,

k 1, 2,..., m.

Уравнения (1.31) называются уравнениями Эйлера-Лагранжа.

Если граничные условия не заданы, система уравнений (1.31)

дополняется условиями трансверсальности типа (1.25), в которых вместо F

необходимо подставить H.

i y'

i 1

t 0

y'i

yi0

i 1

В случае неголономных связей вариационные задачи решаются аналогично.

2.8. Вариационные задачи с изопериметрическими условиями.

Рассмотрим задачу нахождения экстремума функционала (1.28) при наличии изопериметрических связей

	t1
Jk	Fk (t, y1(t),..., yn (t), y'i (t), ..., y'n (t))dt ck ,	k 1, 2,..., m ,	(1.32)
	t0
где ck	- заданные постоянные величины.

Такие связи не накладывают ограничений на вариации функций y(t) в

текущий момент времени, они являются интегральными, поэтому число связей может быть и больше, чем число функций, т.е. m > < n.

Вариационная задача с ограничениями (1.32) может быть сведена к задаче

с неголономными связями, если ввести новые переменные

zk (t) Fk ( , y( ), y'( ))d ,

t t .

(1.33)

Из (1.33) следует, что вектор-функция

zk (t)

удовлетворяет системе

уравнений

d zk

F (t, y(t), y /(t)),

) 0,

) c

(1.34)

Введем функции H и H *

m	m
H * F k [Fk (t, y(t), y'(t)) z'k ],	H (t) F k Fk .
k 1	k 1

Тогда H * H k z'k и задача минимизации функционала J сводится

кзадаче минимизации функционала J *

J J * H * (t, y(t), y' (t), z' (t))dt

(1.35)

Уравнения Эйлера-Лагранжа будут иметь вид:

d H *

dt y'i

(1.36)

d H *

dt z'k

Так как H* не зависит от z(t) , то

d H *

k 0 . Значит

dt z'

k const .

Таким образом, множители Лагранжа в вариационной задаче с изопериметрическими условиями являются постоянными величинами, для определения которых имеется система (1.32). При этом система уравнений Эйлера-Лагранжа (1.36) может быть записана в виде

H	d	H	0,	i 1,..., n .	(1.37)

yi	dt y'i

Система управлений (1.37) должна решаться совместно с условиями

(1.32) и граничными условиями, вытекающими из условия трансверсальности.

Пример. Рассматривая задачу минимизации волнового сопротивления

a
J K y'2 dt	(1.38)

было показано, что уравнение оптимального профиля имеет вид

y ah t .

Рассмотрим теперь задачу минимизации функционала (1.38) при условии y(0) 0, y(a) 0 и заданной площади профиля S

S J1 y (t) dt c1,

c1 0 .

(1.39)

В данном случае H F F Ky'2

y(t) и уравнение Эйлера-

Лагранжа будет иметь вид

y''

t c ,

t 2 c t c

Таким образом, оптимальный профиль имеет параболическую форму.

Параметры профиля

( 1 с1, с2 )

находятся из граничных условий и условия

(1.39)

2.9. Необходимое и достаточное условие относительного экстремума.

Рассмотрим некоторый функционал I I [ y(t)], где y(t) ( y1(t), y2 (t), ... yn (t)), и приращение его представим в виде

I I 12 2 I O( y) ,

где 2 I - вторая вариация функционала, O( y) - величина более высокого порядка малости, чем 2 I , т.е. limO( y) 2 I 0 при 2 I 0 и lim 2 I 0 при

y 0. Безусловно, предполагается способ приближения y к нулю заданным.

Рассмотрим такую достаточно малую окрестность экстремали, что

2( O( y) 2 I ) 1 .

Тогда знаки приращения I и второй вариации 2 I совпадают.

Если I 0, то 2 I 0 , и если 2 I 0 , то I 0. Таким образом, если

O( y)	- величина более высокого порядка малости, чем 2 I , то для достижения
относительно минимума необходимо и достаточно, чтобы
	I 0,	2 I 0 .	(1.40)

2.10. Необходимое условие Лежандра Рассмотрим задачу нахождения экстремума простейшего функционала

t1
I F (t, y(t), y'(t)) dt	(1.41)
t0

с закрепленными концами. Докажем, что для достижения относительного минимума необходимо

2 F	0	,	(1.42)
y'2	0	,	(1.42)
y'2
а для максимума – условие
2 F	0 .		(1.43)
y'2	0 .		(1.43)
y'2

Неравенства (1.42) и (1.43) называются условиями Лежандра. Используя формулу Тейлора, найдем

y y'

2 I

F2 y2 2

F2 y'2 dt .

y y'

Предполагается, что отброшенные нелинейные члены более высокого

порядка малости, чем 2 I . Тогда знак I определяется знаком 2 I .

Используя равенства

2 y y'

d y2

( y)t t

2 2 F

y y'

для второй вариации 2 I

2 F

y y'

получим выражение

2 I

y'2

dt .

y'2

y y'

Введем обозначения

2 F

2 Q.

y y'

Тогда 2 I представим в виде

2 I (P y2 Q y'2 ) dt .

Убедимся, что для достижения

минимума

I ,

если

он

существует,

необходимо Q 0. Для этого покажем,

что если Q 0,

то всегда можно найти

такую функцию y(t) с кусочно-непрерывной производной,

что

2 I 0 , т.е.

всегда можно построить такую кривую сравнения,

что знак 2 I

определится

знаком непрерывной функции Q .

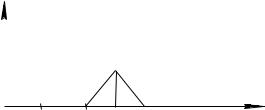
Пусть 2 I 0 , т.е. достигается минимум функционала, и допустим, что в некоторой точке t* (t0 ,t1 ) выполняется неравенство (Q)t * Q* 0 . Тогда Q 0

в силу непрерывности Q по t в некоторой окрестности (t* , t* ) этой точки

t* . Зададимся (рис. 9):

y 2 (1	1	t t*	), t (t* , t* ) ;
	1


y 0, t (t* , t* ) .
Тогда

при t (t* , t* ),	max	y	2 , и, следовательно, будем иметь:
при t (t* , t* ),	max	y	2 , и, следовательно, будем иметь:
				t*
			2 I	(P y2 2Q) dt .

Но y2 4 , поэтому при достаточно малом, но положительном получим:

P y2 Q 0, I 2 0 .

Это противоречит 2 I 0

I 0 . Следовательно, для достижения

относительного и слабого экстремума

необходимо, чтобы Q 0. Аналогично

доказывается необходимость Q 0

для

t1 t

достижения

максимума.

Эти

Рис. 9

необходимые

условия максимума и

минимума более сильны, чем уравнения Эйлера, которые не могут различать максимума от минимума. Условия Лежандра используются совместно с уравнениями Эйлера, и при помощи их различают максимум и минимум.

Если функция

зависит

от

нескольких аргументов, т.е.

F F(t, y1, y2 ,..., yn , y'1 , y'2 ,..., y'n ) ,

то условие Лежандра

значительно

усложняется. Для минимума это запишется так:

y'i y' j 0,

(1.44)

i, j 1

y'i ' j

а для максимума

y'i y' j 0

(1.45)

y'i '

i, j 1

в каждой точке t [a,b] при произвольных y'i

(i 1, 2,..., n) . Так как эти условия

неудобны для использования, их приводят к виду (условия Сильвестра)

2 F

y'1 y'1

y'1 y'2

0,....

(1.46)

y'1 y'1

2 F

y'2 y'1

y'2 y'2

Вопросы для контроля

1.Понятие функционала, виды функционалов.

2.Понятие меры близости функций, абсолютного и относительного минимума.

3.Необходимое условие относительного минимума.

4.Основная лемма вариационного исчисления.

5.Уравнение Эйлера (для заданного функционала).

6.Условие трансверсальности (для конкретного случая).

7.Условный экстремум, виды связей, методы решения.

8.Решение задачи при изопериметрических условиях.

9.Необходимые и достаточные условия относительного минимума.

10.Условие Лежандра.

Задачи

1. Найти экстремали функционалов:

		− ′3) ,
= ∫	( ′	− ′3) ,	( ) = ,	( ) = ;
			1	2


= ∫	( ′2	+ 2 ′) ,	( ) = ,	( ) = ;
			1	2

1		+ ′2) ,
= ∫ ( 2		+ ′2) ,	(0) = 1,	(1) = ;
0
1	( ′2
= ∫	( ′2	+ 12 ) ,	(0) = 0,	(1) = 1 ;
0
⁄2
= ∫	( ′2 − 2) ,		(0) = 0,	(1) = 1 .
0

2. Записать условие трансверсальности в задаче:


= ∫ ′2 → ,	(0) = 0,	( ) + + 1 = 0 .

<<< < Предыдущая 1 23 / 83 4 5 6 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.08.2019156.16 Кб1ГЭК2012.doc
#
23.05.2015341.14 Кб68ДP с АГНИ.docx
#
27.11.201914.32 Mб78Данилаев лекции САЭУ.doc
#
12.03.2015411.14 Кб31Двухтактный_цикл.doc
#
12.03.201566.05 Кб19девник практики для всех.doc
#
22.03.20161.68 Mб63Дегтярёв Оптимальное управление.pdf
#
07.09.2019149.5 Кб6Декларирование соответствия.doc
#
12.03.201572.7 Кб307Дерево отказов - пожар.doc
#
12.03.20153.92 Mб57Детали машин - пояснительная записка.doc
#
08.05.201910.31 Mб49ДЕТАЛИ МАШИН.doc
#
12.03.2015987.69 Кб34детмаш.docx