Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский национальный исследовательский технический университет им. А. Н. Туполева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Стрежнева

.pdf

Скачиваний:

Добавлен:

22.03.2016

Размер:

605.49 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 86 7 8 > Следующая >>>

A = a ,

= 0

, A

= A =

+ b2

− k

= −ϕ

, k = 1, 2,3..., (15.1)

0 0

− k

выводим

− ib

) =

( A cos ϕ

− iA sin ϕ

)

(cos ϕ

− i sin ϕ

)

e−iϕk

k = 1, 2,3...

;

= a0

c =

e−iϕk , k = 0

;

ϕ0

− k

+ ib

) =

( A cos ϕ

+ iA sin ϕ

) =

(cos ϕk

+ i sin ϕk ) =

eiϕk ,

k = 1,2,3...

A− k

eiϕ− k =

e−iϕk

k = −1, −2, −3...

Следовательно, имеем единую формулу для коэффициентов ck ряда Фурье в комплексной форме при любом значении индекса суммирования k:

c =	Ak	e−iϕk	, k = 0, ± 1, ± 2, ± 3 ...	(15.2)

k	2

Таким образом, ряд Фурье в комплексной форме (5.3) можно представить в эквивалентном виде


		∞			∞
f (x ) = ∑ ck eikωx = ∑						Ak		e−iϕk eikωx = {ωk = kω} =
f (x ) = ∑ ck eikωx = ∑								e−iϕk eikωx = {ωk = kω} =
		k =−∞			k =−∞ 2
		∞						∞
	= ∑		Ak		e−iϕk eiωk x =			∑	Ak	ei ( ωk x−ϕk ) =
	= ∑				e−iϕk eiωk x =			∑		ei ( ωk x−ϕk ) =
		k =−∞		2			k =−∞ 2
	1	∞		(cos(ωk x − ϕk ) + i sin(ωk x − ϕk )).
=	1	∑ Ak
=		∑ Ak
	2 k =−∞

Каждый член этого ряда называется комплексным гармоническим колебанием, коэффициент ck – комплексной амплитудой,

ωk – частотой.

Таким образом, разложение периодической функции f (x) в ряд Фурье также эквивалентно представлению ее в виде бесконечной суммы комплексных гармонических колебаний (комплексных гармоник).

16. Спектральные характеристики комплексной формы

ряда Фурье

Дадим определения спектров комплексной формы ряда Фурье для периодической функции f (x) с периодом T .

Определение. Частотными спектрами называются последо-

вательности

				{ωk }, {νk } ,			(16.1)
где ωk	= kω; ω =	2π	и νk	= kν; ν =	1	при k = ±1, ± 2, ± 3,...

		T			T

Геометрическая иллюстрация частотных спектров (16.1) приведена на рис. 16.1. Частотные спектры строятся следующим образом: на оси абсцисс откладываются числа k = ±1, ±2, ±3... и от каждой точки k проводится перпендикулярно оси абсцисс отрезок величиной ωk или νk . Эти спектры нечетно-симметричны.

Определение. Линейчатыми спектрами называются после-

довательности

{2 Re{ck }}−−∞1 U{2 Re{ck }}1+∞ и {2 Im{ck }}−−∞1 U{−2 Im{ck }}1+∞ . (16.2)

Рис. 16.1

Замечание. Линейчатые спектры комплексной формы ряда Фурье связаны с линейчатыми спектрами вещественной формы, что следует из формул (3.1). Действительно,

−1

+∞

{2 Re{ck }}−∞

= {2 Re{c− k

}}1

= 2 Re

(ak

+ ibk )

= {ak }1

;

+∞

{2 Re{ck }}1

= 2 Re

(ak − ibk )

= {ak }1

т.е.

2 Re{c−1} = 2 Re{c1} = a1; 2 Re{c−2 } = 2 Re{c2 } = a2 ;

2 Re{c−3} = 2 Re{c3} = a3 ...

Аналогично,

−1

+∞

{2 Im{ck }}−∞

= {2 Im{c− k

}}1

= 2 Im

(ak

+ ibk )

= {bk }1

;

+∞

{−2 Im{ck }}1

−2 Im

(ak

− ibk )

= {bk }1

т.е.

2 Im{c−1} = −2 Im{c1} = b1; 2 Im{c−2 } = −2 Im{c2 } = b2 ;

2 Im{c−3} = −2 Im{c3} = b3 ...

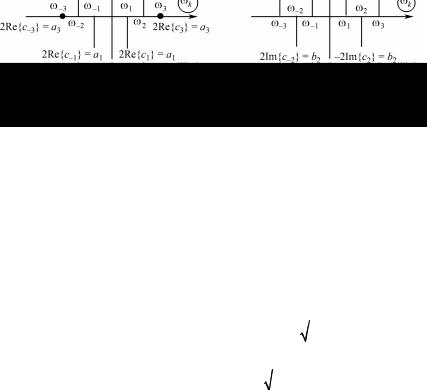
Геометрическая иллюстрация линейчатых спектров (16.2) приведена на рис. 16.2. Линейчатые спектры строятся следующим образом: на оси абсцисс откладываются частоты ωk и от каждой

точки ωk проводится перпендикулярно оси абсцисс отрезок величи-

ной 2 Re{ck } или 2 Im{ck }, k = −1, −2,−3,...; −2 Im{ck }, k = 1,2,3,....

Эти спектры четно-симметричны.

Рис. 16.2

Определение. Амплитудно-частотным спектром называется последовательность

{2 | ck |}−∞−1 U{2 | ck |}1+∞.

(16.3)

Замечание. АЧХ комплексной формы ряда Фурье связаны с АЧХ вещественной формы, что следует из формул (3.1) и (14.2). Действительно,

−1

+∞

{2 | ck |}−∞ =

{2 |c−k

|}1

= 2mod

(ak + ibk )

= {

+ bk

}

= {Ak }1

;

+∞

{2 |ck

|}1+∞ =

2 mod

(ak

− ibk )

= { ak2 + bk2 }

= {Ak }1+∞ ,

т.е. 2 | c−1 |= 2 | c1 |= A1;

2 | c−2 |= 2 | c2 |= A2 ; 2 | c−3 |= 2 | c3 |= A3...

Геометрическая иллюстрация АЧХ (16.3) приведена на рис. 16.3. Эти спектры четно-симметричны.

Рис. 16.3

Определение. Фазово-частотным спектром называется по-

следовательность

{− arg ck }−∞−1 U{− arg ck }1+∞ .

(16.4)

Замечание. ФЧХ комплексной формы ряда Фурье связаны с ФЧХ вещественной формы, что следует из формул (3.1) и (13.4). Действительно,

−1

+∞

{− arg ck }−∞

= {− arg c− k

= − arg

(ak

+ ibk )

= {−ϕk }1

;

+∞

{− arg ck }1

= − arg

(ak − ibk )

= {−(−ϕk )}1

= {ϕk }1

т.е.

− arg c−1 = −ϕ1; − arg c1 = ϕ1;	− arg c−2	= −ϕ2 ; − arg c2 = ϕ2 ;
− arg c−3 = −ϕ3;	− arg c3	= ϕ3 ...

Геометрическая иллюстрация ФЧХ (16.4) приведена на рис. 16.4. Эти спектры нечетно-симметричны.

Рис. 16.4

Далее в комплексной записи ряда Фурье

							∞	∞
						f (x ) = ∑ ck eikωx = ∑ ck eiωk x ,
							k =−∞	k =−∞
где ck	=	1	α+T	f (x)e−iωk x dx (k = ±1,±2,...).
где ck	=	T	∫α	f (x)e−iωk x dx (k = ±1,±2,...).
		T	∫α
	Перейдем к измеряемой в герцах частоте
ношению ωk				= 2πvk . Получим
							f (x)	+∞
							f (x)	= ∑ ck ei 2πvk x ,
								k =−∞
где c	= c (v ) =				1	α+T	f (x)e−i 2πvk x dx .
где c	= c (v ) =				T	∫α	f (x)e−i 2πvk x dx .
k			k		T	∫α
k			k

vk согласно соот-

(16.5)

Разложение (16.5) показывает, что периодическая функция f (x) может быть выражена через частотные составляющие

c ei 2πvk x	с частотами v ,	v	2	= 2v , ..., v	k	= kv ,..., образующими ее
k	1		2	1	k	1

спектр частот.

S (vk ) .

= ρ (vk )

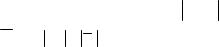
Таким образом, если дана функция f (x), то можно определить ее спектр частот. Справедливо и обратное: по известному спектру частот можно найти соответствующую периодическую функцию.

В связи со сказанным вводится понятие спектральной функции ряда Фурье.

Определение. Спектральной функцией или спектральной плотностью S (vk ) ряда Фурье называется отношение комплекс-

ной амплитуды (коэффициента Фурье) ck = c (vk )

функции f (x) пе-

риода T к приращению частоты

vk :

vk = vk +1 − vk

k + 1

−

(16.6)

T T

т.е.

S (vk ) =

c (vk )

α+T

(x )e−i 2πvk x dx .

= ∫ f

(16.7)

Из (16.6) видим, что частоты гармоник образуют бесконеч-

ную арифметическую прогрессию с разностью

Определение. Амплитудным спектром ρ(vk ) называется мо-

дуль спектральной функции

ρ(vk ) =

S (vk )

= T

c (vk )

(16.8)

Графическое изображение амплитудного спектра дано на рис. 16.5. Амплитудный спектр строится следующим образом: на оси абсцисс откладываются частоты vk и от каждой точки vk про-

водится перпендикулярно оси абсцисс отрезок величиной

Так как S (vk ) = Tc (vk ) и c− k = ck , то c− k = ck , т.е. ρ(v− k )

и амплитудный спектр симметричен относительно оси ординат – четно симметричен.

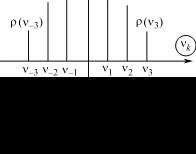
Рис. 16.5

Определение. Фазовым спектром Φ (vk ) называется взятый

с обратным знаком аргумент спектральной функции
Φ (vk ) = − arg S (vk ).	(16.9)
Аналогично строится фазовый спектр периодической функ-
ции f (x) с той только разницей, что отрезки длины Φ (vk )	отклады-

ваются вверх от точки vk при Φ (vk ) > 0 и вниз Φ (vk ) < 0.

Спектры существуют только в частотах v1, v2 = 2v1,...,vk = kv1,...

иих нельзя изобразить непрерывной кривой. Графики спектров периодических функций имеют вид диаграмм и называются, как

исами спектры, линейчатыми.

17. Пример построения спектральных характеристик комплексной формы ряда Фурье

Пример. Построить спектральные характеристики комплексной формы ряда Фурье для функции

( ) A, при 0 ≤ x < T / 2;

f x = при ≤ <

0, T / 2 x T , где A > 0, A − const, f (x + T ) = f ( x) (рис. 17.1).

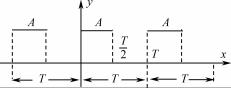
Рис. 17.1

Найдем коэффициенты комплексной формы ряда Фурье:

α+T

Ae−iωk x dx + T

e−iωk x

c =

f (x)e−iωk x dx =

0e−iωk x dx

2 =

∫

T −iω

i2 = −1

−iωk

2 −1) i

2π

(e−ikπ −1)i

A(e−ikπ −1)i

ω = kω = k

−iωk i

2π

2πk

2π

= k

= kπ

T 2

k 2

e−ikπ = cos kπ − i sin kπ

A(cos kπ − 1)i

kπ

1− cos kπ

= sin

sin kπ = 0

2πk

= −

sin2

kπ

, c = −

, c

= c

= 0,

, c = −

...

πk

−1

−2

−3

3π

2 Re{c } = 0, k = ±1, ± 2, ± 3... 2Im{c } = −2 Im{c } =

−1

2 Im{c

−2

} = −2 Im{c2} = 0,

2 Im{c

−3

} = −2 Im{c } =

...

3π

2 | c

| = 2 | c | =

, 2 | c

= 2 | c

| = 0, 2 | c

−3

| = 2 | c |=

;

−1

−2

3π

− arg{c−1} = − arg{c1} = π , − arg{c−2 } = − arg{c2} = 0, 2

− arg{c−3} = − arg{c3} = π ...

	AT	πk	πvk	, k = 1,

ρ(vk ) =		sin	, Φ (vk ) =	k = 2;	Φ(vk +T ) = Φ(vk ).
	πk
		2	0,

18. Тестовые задания на тему «Ряды Фурье»

Вопрос № 1. Какие из следующих формул:

1)	b	=	2		T		f		(x)sin kωxdx (k N ),
1)	b	=	T		∫		f		(x)sin kωxdx (k N ),
	k		T		∫			n
	k							n
					0
	ak	=		2		T	fn (x)cos kωxdx (k N );
	ak	=		T		∫	fn (x)cos kωxdx (k N );
				T		∫
					0
2) c =			1		T		f		(x)e−ikωx dx (k Z );
2) c =			T		∫		f		(x)e−ikωx dx (k Z );
	k		T		∫			n
	k							n
					0
3)	b	=	2		α+T				f (x)sin kωxdx	(k N ),
3)	b	=	T			∫α			f (x)sin kωxdx	(k N ),
	k		T			∫α			n
	k								n
	ak	=		2		α+T			fn (x)cos kωxdx	(k N )
	ak	=		T		∫α			fn (x)cos kωxdx	(k N )
				T		∫α

являются формулами Эйлера – Фурье в вещественной форме?

Ответ:

1. 1) и 2). 2. 2) и 3). 3. 1) и 3). 4. только 2). 5. нет верного ответа.

	a0	∞
Вопрос № 2. Формула f (x) ~		+ ∑(ak cos kωx + bk sin kωx),

2		k =1

в которой коэффициенты находятся по формулам Эйлера – Фурье, дает для функции f (x) ряд Тейлора.

<<< < Предыдущая 1 2 3 4 56 / 86 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
25.11.2019167.42 Кб2СТО СМК 01-2012.doc
#
12.03.201521.5 Кб9стр 12 (Задача 2.1).doc
#
12.03.201525.09 Кб23стр 13 (Задача 2.2 и 2.3).doc
#
12.03.201523.55 Кб15стр 7 (Задача 1.1).doc
#
24.11.2019130.05 Кб2стратег планир Залакова.doc
#
22.03.2016605.49 Кб19Стрежнева.pdf
#
27.09.201993.25 Кб1Структура философии.docx
#
12.03.20151.81 Mб348Структуры и алгоритмы обработки данных.doc
#
12.03.2015835.7 Кб18Сттатистические методы управления качеством.pdf
#
19.12.20186.64 Mб14СУсЧПУ_1201_Ведерников.doc
#
22.07.2019377.85 Кб5СУХТП_Венера.docx