
Стрежнева
.pdf
Пусть точка (a,b) ÎIV лежит в четвертой четверти (рис. 13.1 б). Обозначим через α угол ÐBAC в прямоугольном треугольнике ABC . Пусть a = -j, j < 0, т.е. угол ϕ отсчитывается по часовой
стрелке от оси Ox (рис. 13.1, б). Тогда в прямоугольном треугольнике DABC длины катетов равны: | AB |= a, | BC |= -b, а гипотенуза
| AC |= |
|
. Следовательно, cosα = |
|
a |
|
, sin α = |
|
−b |
|
|
|
a2 + b2 |
|
и, |
|||||||||
|
|
|
|
|
|
||||||
a2 + b2 |
a2 + b2 |
||||||||||
|
|
|
|
|
|
|
|
|
принимая во внимание четность функции косинус и нечетность функции синус, имеем:
cos α = cos(−ϕ) = cos ϕ = |
|
a |
|
|
|
|||||
|
|
; |
|
|
|
|
||||
|
|
|
|
|
||||||
|
|
−b |
|
a2 + b2 |
|
|
|
|||
sin α = sin(−ϕ) = −sin ϕ = |
|
sin ϕ = |
|
b |
||||||
|
|
|
|
|
|
. |
||||
|
|
|
|
|
|
|||||
|
|
a2 + b2 |
|
|
|
|
a2 |
+ b2 |
||
Доказали справедливость соотношений (13.1) для четверти IV.
Кроме того, tg α = −b tg(−ϕ) = −b tg ϕ = |
b |
ϕ = arctg |
b |
, что |
|
a |
|
||||
a |
a |
|
a |
||
доказывает (13.2).
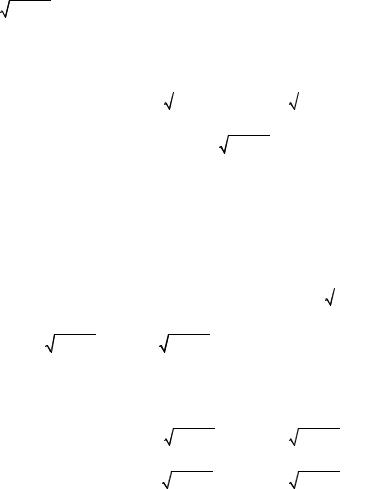
Проведем аналогичные рассуждения для четверти II (рис. 13.2, а).
Рис. 13.2
В прямоугольном треугольнике |
ABC длины катетов равны: |
|||||
| AB |= −a, | BC |= b, а гипотенуза | AC |= |
|
. Тогда cosα = |
|
−a |
|
|
a2 +b2 |
|
, |
||||
|
|
|
||||
|
|
|
|
a2 + b2 |
||
|
|
|
|
|
41 |
|
|
|
b |
|
||
sin α = |
|
|
|
, где α – |
угол ÐBAC . Пусть ϕ + α = π, ϕ > 0, т.е. |
|
|
|
|||
|
|
a2 |
+ b2 |
|
|
угол ϕ отсчитывается от оси Ox против часовой стрелки (рис. 13.2, а). Следовательно,
cos α = cos(π − ϕ) = − cos ϕ = |
|
|
−a |
|
|
|
|
cos ϕ = |
|
a |
|
; |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a2 + b2 |
|
|
|
|
a2 + b2 |
||||||||||
|
|
|
|
sin α = sin(π − ϕ) = sin ϕ = |
|
|
b |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 + b2 |
|
|
|
|
|
|
||
Кроме того, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
b |
|
|
|
|
b |
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
b |
|||
tg α = |
|
α = arctg |
|
= −arctg |
|
ϕ = π − α = π + arctg |
|
. |
|
||||||||||||||||||
−a |
|
a |
|
||||||||||||||||||||||||
|
|
|
|
|
−a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|||||
Формулы (13.1), (13.2) доказаны для четверти II. |
|
|
|
|
|
|
|||||||||||||||||||||
Рассмотрим случай четверти III (см. рис. 13.2, б). В пря- |
|||||||||||||||||||||||||||
моугольном |
треугольнике |
|
|
ABC |
|
длины катетов |
равны: |
||||||||||||||||||||
| AB |= −a, | BC |= −b, α – |
|
|
|
|
гипотенуза | AC |= |
|
. |
||||||||||||||||||||
угол |
ÐBAC , |
a2 + b2 |
|||||||||||||||||||||||||
Тогда cos α = |
|
−a |
sin α = |
|
|
|
|
−b |
|
|
|
|
|
Пусть −ϕ + α = π, ϕ < 0, |
|||||||||||||
|
|
, |
|
|
|
|
|
|
|
. |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
a2 + b2 |
|
|
|
|
|
a2 + b2 |
|
|
|
|
|
|
|
|
|
|
|||||||
т.е. угол ϕ отсчитывается от оси Ox по часовой стрелке (рис. 13.2, б). Следовательно,
cos α = cos(π + ϕ) = − cos ϕ = |
|
|
−a |
cos ϕ = |
|
a |
|||||
|
|
|
|
|
|
|
|
; |
|||
|
|
|
|
|
|
|
|
||||
|
|
|
|
a2 |
+ b2 |
|
|
a2 |
+ b2 |
||
sin α = sin(π + ϕ) = − sin ϕ = |
|
|
|
−b |
sin ϕ = |
|
b |
||||
|
|
|
|
|
|
|
|
|
. |
||
|
|
|
|
|
|
|
|
|
|||
|
|
|
a2 |
+ b2 |
|
|
a2 |
+ b2 |
|||
Доказаны формулы (13.1). Найдем тангенс угла в прямоугольном треугольнике DABC :
tg α = |
−b |
α = arctg |
b |
ϕ = α − π = arctg |
b |
− π. |
−a |
a |
|
||||
|
|
|
a |
|||
42
Последнее соотношение доказывает формулы (13.2) для четверти III.
Теорема 13.1 доказана.
Замечание. Теорема 13.1 формулировалась для точки (a,b), лежащей в координатных углах. Если точка (a,b) лежит на координатных осях, т.е. хотя бы одна из координат обращается в ноль, соотношения (13.1) остаются справедливыми, но вместо формулы (13.2) имеет место другое соотношение, определяющее угол ϕ:
0 , |
если |
a ³ 0, |
b = 0; |
||
|
|
|
|
|
|
p , |
если |
a = 0, |
b > 0; |
||
|
2 |
|
|
|
(13.3) |
j = |
|
|
|
a < 0, |
|
p, |
если |
b = 0; |
|||
|
- |
p |
,если |
a = 0, |
b < 0. |
|
2 |
||||
|
|
|
|
|
|
Ñ
Действительно, если a ³ 0 , b = 0, то j = 0 и, следовательно, cos j = 1, sin j = 0. Это равносильно соотношениям (13.1), так как
cos j = |
|
|
a |
|
|
|
|
= |
|
|
|
|
a |
|
|
|
= |
|
a |
= |
|
a |
= 1; |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| a | |
|
|
||||||||||||
|
|
|
|
a2 + b2 |
|
|
|
|
|
|
|
a2 + 02 |
|
|
|
|
|
a |
|||||||||||||||
sin j = |
|
|
|
b |
|
|
= |
|
|
0 |
|
|
|
= 0. |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
a2 |
|
|
+ b2 |
|
a2 |
+ 02 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Если a = 0, b > 0, то |
|
|
j = p и, |
|
следовательно, cos ϕ = 0, |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
sin ϕ = 1. Это равносильно соотношениям (13.1), так как |
|||||||||||||||||||||||||||||||||
cos j = |
|
|
|
a |
|
|
= |
|
|
|
|
0 |
|
|
|
|
= 0; |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
a2 |
|
+ b2 |
|
|
|
|
|
02 |
|
+ b2 |
|
|
|
|
|
||||||||||
sin j = |
|
|
|
b |
|
|
|
= |
|
|
|
|
b |
|
|
= |
|
b |
|
= |
b |
= 1. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| b | |
|
||||||||||||||
|
|
|
a2 + b2 |
|
|
|
|
|
02 + b2 |
|
|
|
b |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
43 |
||||
Если |
a < 0 , |
|
b = 0, |
|
то |
ϕ = π |
и, следовательно, |
cos ϕ = −1, |
||||||||||||||||||||||||
sin ϕ = 0. Это равносильно соотношениям (13.1), так как |
|
|||||||||||||||||||||||||||||||
|
cos ϕ = |
|
|
|
a |
|
|
|
|
= |
|
|
|
|
a |
|
|
|
= |
|
a |
= |
|
a |
= −1; |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
a2 + b2 |
|
|
|
a2 + 02 |
|
| a | |
|
|
|
|
−a |
|
|||||||||||||||
|
sin ϕ = |
|
|
|
|
b |
|
|
|
|
= |
|
|
0 |
|
|
|
|
= 0. |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
a2 + b2 |
|
a2 + 02 |
|
|
|
|
|
|
|
|
||||||||||||||
Если |
a = 0, |
b < 0, |
|
то |
ϕ = − π |
|
|
|
и, |
|
следовательно, |
cos ϕ = 0, |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
sin ϕ = −1. Это равносильно соотношениям (13.1), так как |
|
|||||||||||||||||||||||||||||||
|
cos ϕ = |
|
|
|
|
a |
|
|
|
|
= |
|
|
0 |
|
|
|
|
= 0; |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
a2 + b2 |
|
|
02 + b2 |
|
|
|
|
|
|
|
|
||||||||||||
|
sin ϕ = |
|
|
|
b |
|
= |
|
|
|
|
b |
|
= |
|
b |
= |
b |
= −1. |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
a2 + b2 |
|
|
02 + b2 |
| b | |
|
|
|
−b |
|
|||||||||||||||||||
Следствие 13.1. Для двух произвольных действительных чисел a, b , существует такой угол ϕ (−π, π], что справедливы
соотношения (13.1), причем этот угол определяется формула-
ми (13.2) или (13.3).
Геометрические иллюстрации возможных значений угла ϕ даны на рис. 13.3. Из них видно, что ϕk является аргументом комплексного числа ak + ibk :
ϕk = arg (ak + ibk ). |
(13.4) |
Преобразуем выражение, стоящее под знаком суммы в ряде Фурье в вещественной форме (5.1):
|
|
|
|
ak cos kωx + bk sin kωx = |
||||||
|
|
|
|
|
ak |
|
|
bk |
||
= a2 |
+ b2 |
|
|
cos kωx + |
|
|||||
|
|
|
|
|
||||||
|
k |
k |
|
2 |
2 |
2 |
2 |
|||
|
|
|
|
|
ak |
+ bk |
|
|
ak |
+ bk |
sin kωx . (13.5)
44

ϕ(– π, π]
Рис. 13.3
Согласно следствию 13.1, существует такой угол ϕk (−π,π],
что |
cosϕk = |
|
ak |
|
; sin ϕk |
= |
|
bk |
|
, |
который можно найти по |
|||
|
|
|
|
|
|
|
|
|||||||
a2 |
+ b2 |
a2 |
+ b2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
k |
k |
|
|
|
|
k |
k |
|
|
|
|
формулам (13.2) или (13.3). Следовательно, соотношение (13.5), используя формулу тригонометрии cos(α − β) = cos α cosβ +
+sin αsin β , можно записать в следующем виде:
|
|
cos kωx + b sin kωx = |
|
|
(cos ϕ |
|
cos kωx + sin ϕ |
|
sin kωx) = |
|||||||||
a |
k |
a2 |
+ b2 |
k |
k |
|||||||||||||
|
|
|
k |
k |
|
k |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
a |
2 |
+ b |
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||||
= |
|
|
|
A |
|
|
|
|
= Ak |
cos(ωk x − ϕk ), |
||||||||
ak2 + bk2 cos(kωx − ϕk ) = |
k |
|
|
k |
|
k |
|
|||||||||||
|
|
|
|
|
|
ω |
k |
= kωx |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
известном в разнообразных приложениях как гармоническое колебание (гармоника) с амплитудой Ak , частотой ωk и фазой ϕk . Таким
образом, разложение периодической функции в ряд Фурье (5.1) эквивалентно представлению ее в виде бесконечной суммы гармоник
|
a0 |
|
∞ |
|
||
f (x ) = |
+ ∑(ak cos kωx + bk sin kωx) = |
|
||||
|
|
|
||||
2 |
|
k=1 |
|
|||
|
|
a0 |
∞ |
|
||
= |
+ ∑ Ak cos (ωk x − ϕk ), |
(13.6) |
||||
|
||||||
2 |
k =1 |
|
||||
амплитуды которых Ak и фазы ϕk определяются коэффициентами Фурье ak и bk , при этом
ak = Ak cos ϕk ; bk = Ak sin ϕk , k = 1,2,3... |
(13.7) |
|
45 |

14. Спектральные характеристики вещественной формы ряда Фурье
Дадим определения спектров вещественной формы ряда Фурье для периодической функции f (x) с периодом T .
Определение. Частотными спектрами называются последо-
вательности {ω |
}∞ |
, |
{ν |
}∞ , где ω |
|
= kω; ω = |
2π |
и ν |
|
= kν; ν = |
1 |
. |
||||||||||||
k |
|
k |
|
|||||||||||||||||||||
|
|
|
k |
1 |
|
|
k |
1 |
|
|
|
|
|
T |
|
|
|
|
|
T |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Определение. Линейчатыми спектрами называются после- |
||||||||||||||||||||||||
довательности {a |
}∞ , {b |
}∞ , где |
|
a |
k |
и |
b определяются соотноше- |
|||||||||||||||||
|
|
|
|
k |
1 |
k |
1 |
|
|
|
k |
|
|
|
|
|
|
|
|
|||||
ниями: |
|
|
|
|
|
|
α+T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ak |
|
= |
2 |
f (x)cos kωx dx |
(k = 0, 1, 2, 3...); |
|
|
|
||||||||||||||
|
|
T |
∫α |
(14.1) |
||||||||||||||||||||
|
|
α+T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2 |
|
(x )sin kω x dx (k = 1, 2, 3,...), ω = |
2π |
|
|||||||||||||||||||
b = |
f |
, |
α . |
|||||||||||||||||||||
|
|
|||||||||||||||||||||||
k |
T ∫α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Определение. Амплитудно-частотным спектром (АЧХ – амплитудно-частотной характеристикой) называется последова-
тельность {A |
}∞ |
, где |
|
|
|
|
k |
1 |
|
|
|
|
|
|
|
A = |
|
|
. |
|
|
|
a2 |
+ b2 |
(14.2) |
||
|
|
k |
k |
k |
|
|
Определение. Фазово-частотным спектром (ФЧХ – фазово-
частотной характеристикой) называется последовательность {ϕk }1∞, где ϕk определяются соотношениями:
|
|
b |
|
если (a,b) четверти I, IV, т.е. ak > 0, bk , |
|||
|
arctg |
k |
, |
||||
|
ak |
||||||
|
|
|
|
|
|
||
|
|
bk |
|
|
|
|
|
ϕk |
= arctg |
+ π, |
если (a,b) четверти II, т.е. ak |
< 0, bk |
> 0, (14.3) |
||
ak |
|||||||
|
|
|
|
|
|
||
|
|
bk |
− π, |
если (a,b) четверти III, т.е. ak |
< 0, bk |
< 0; |
|
|
arctg |
||||||
|
ak |
||||||
|
|
|
|
|
|
||
46
|
0 , |
если |
ak |
³ 0, |
bk |
= 0, |
||
|
|
|
|
|
|
|
|
|
|
p , |
если |
ak |
= 0, |
bk |
> 0, |
||
jk |
|
2 |
|
|
|
|
|
(14.3) |
= |
|
|
|
ak |
< 0, |
bk |
||
|
p, |
если |
= 0, |
|||||
|
|
|
p |
если ak |
= 0, |
bk |
< 0. |
|
|
- |
2 |
||||||
|
|
|
|
|
|
|
|
|
Заметим, что все введенные ранее спектры являются линейчатыми.
Пример 14.1. Разложить в ряд Фурье в вещественной форме функцию
p , |
x Î[-2,0]; |
|
f (x ) = 3 |
p |
|
|
x Î(0,1] |
|
- |
, |
|
|
2 |
|
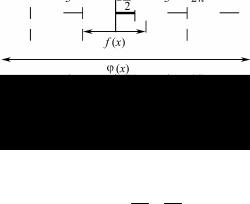
и построить ее спектральные характеристики.
Решение. График функции дан на рис. 14.1, там же приведен график функции j(x) – периодического продолжения функции f (x) с периодом T = 3.
Рис. 14.1
Круговая частота равна w = 2p = 2p . Найдем коэффициенты
T 3
ряда Фурье по формулам (5.2):
47
|
|
|
|
|
|
|
|
|
|
|
2 |
α+T |
|
|
|
|
|
|
|
|
|
|
|
2 |
0 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
a0 |
= |
|
|
∫ f |
(x)dx = |
∫ |
π dx + ∫ − |
π dx = |
π; |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
T |
3 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−2 |
3 |
|
|
|
|
|
0 |
2 |
|
|
|
|
|
|
9 |
|
|
|
||||||||||||
ak |
= |
2 |
α+T |
f (x)cos kωxdx = |
2 |
0 π cos k |
2π |
xdx + |
2 |
|
1 |
− π cos k |
2π |
xdx = |
||||||||||||||||||||||||||||||||||||||||||||
T |
∫α |
|
|
|
|
|
|
|
∫0 |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 −∫2 3 |
|
|
|
|
|
|
|
|
3 |
|
|
3 |
|
|
|
2 |
3 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
1 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
2 π sin k |
2π |
x |
|
|
|
|
|
2 |
|
|
π |
|
sin k |
x |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
− |
|
|
|
|
|
|
3 |
|
|
|
|
|
= |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
3 3 |
|
k |
|
2π |
|
|
|
|
|
3 |
|
|
|
|
k |
|
2π |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2sin |
4πk |
− 3sin |
2πk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(k = 1,2,3...); |
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
b |
= |
2 |
|
α+T |
|
|
f (x ) sin kω x dx |
(k = 1,2,3,...) = |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
T |
∫α |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
2cos |
4πk |
+ 3cos |
2πk |
− 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(k = 1,2,3...). |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Таким образом, разложение в ряд Фурье в вещественной форме для функции f (x) на отрезке [–2,1] принимает вид
|
|
|
|
2sin |
4πk |
− |
3sin |
2πk |
|
|
|
f (x ) = |
π |
∞ |
|
|
|
|
2π |
|
|||
3 |
3 |
|
|
||||||||
+ ∑ |
|
|
|
cos k |
x + |
||||||
|
|
|
6k |
|
|
3 |
|||||
18 |
k =1 |
|
|
|
|
|
|
|
|||
|
2cos |
4πk |
+ 3cos |
2πk |
− 5 |
|
|
|
|
|
|
|
2π |
|
|||
+ |
3 |
3 |
|
|
||||
|
sin k |
x . |
||||||
|
6k |
|
||||||
|
|
|
|
3 |
||||
Построим спектральные характеристики. |
|
|
|
|
|||
Найдем частотные спектры ω |
|
= kω = k |
2π |
и ν |
|
= kν = |
k |
k |
|
k |
|
||||
|
3 |
|
3 |
||||
|
|
|
|
||||
(k = 1,2,3...) (рис. 14.2).
48

Рис. 14.2
Найдем несколько линейчатых спектров и изобразим их на рис. 14.3.
Рис. 14.3
|
|
2sin |
4π |
− 3sin |
2π |
|
|
|
|
|
|
|
|
2sin |
8π |
− 3sin |
4π |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
5 3 |
|
|
|
5 3 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
a = |
3 |
3 |
|
= − |
, a = |
3 |
3 |
|
= |
, |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
1 |
|
|
|
|
|
6 |
|
|
|
2 |
|
|
2 |
|
|
|
|
|
12 |
|
|
|
24 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
a |
= |
2sin 4π − 3sin 2π |
= 0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2cos |
4π |
+ 3cos |
2π |
− 5 |
|
2cos |
8π |
+ 3cos |
4π |
− 5 |
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
b1 = |
|
3 |
|
3 |
|
|
|
= − |
5 |
|
, b2 = |
|
3 |
3 |
|
|
|
= − |
5 |
, |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
6 |
|
|
|
4 |
|
|
|
|
|
|
|
12 |
|
|
|
8 |
|
||||||||||
b3 = 2cos 4π + 3cos 2π − 5 = 0. 18
49
Найдем несколько значений АЧХ, ФЧХ и изобразим их на рис. 14.4.
Рис. 14.4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
+ − |
5 |
2 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 3 |
|
|
|
5 3 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
A = |
|
|
|
|
|
|
|
|
= |
− |
|
|
|
|
|
= |
|
|
|
||||||||||||||||||||
|
|
a2 |
+ b2 |
|
|
|
|
|
|
; |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
1 |
|
1 |
|
1 |
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
+ − |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
5 3 |
5 |
|
|
|
|
|
5 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
A = |
|
|
|
= |
|
|
|
|
|
= |
|
|
|
|
A = |
|
|
|
= 0; |
||||||||||||||||||||||
a2 |
+ b2 |
|
|
|
|
|
; |
|
|
|
a2 |
+ b2 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
2 |
2 |
2 |
|
|
|
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
3 |
|
3 |
3 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−5 |
|
|
|
|
− π = π − π = − |
2π |
|
|
|||||||||||||
|
ϕ =arctg |
b1 |
|
− π = arctg |
|
|
|
4 |
|
|
|
|
; |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
1 |
|
|
|
a1 |
|
|
|
|
|
|
|
− |
5 |
|
3 |
|
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−5 |
|
− π = − π , |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
ϕ |
2 |
=arctg |
b2 |
|
= arctg |
|
|
|
8 |
|
|
ϕ |
3 |
=0. |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
5 3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
15.Связь комплексной формы ряда Фурье
скомплексным гармоническим колебанием
Рассмотрим ряд Фурье в комплексной форме (5.3), (5.4). Из формул (3.1), с учетом (13.7), вводя вспомогательные обозначения
50
