Стрежнева

гонометрический многочлен в вещественной форме может быть записан в виде

4. Формулы Эйлера – Фурье

Введенные коэффициенты ak , bk тригонометрического мно-

гочлена fn (x) в вещественной форме можно выразить через саму

функцию fn (x ).

Умножим левую и правую части формулы тригонометрического многочлена

на sin kωx ( k – натуральное число). Получим выражение:

11

которое интегрируем по переменной x от 0 до Т (при этом вспомним, что интеграл суммы равен сумме интегралов от слагаемых).

Имеем

T

гралы вида ∫sin mωx sin kωxdt кроме одного из них, для которого

0

Аналогично, умножая левую и правую части формулы (4.1) на cos mωx и интегрируя по отрезку [0, T ], получаем

Формулы (4.2), (4.3) представляют собой формулы Эйлера – Фурье в вещественной форме.

12

5. Понятие ряда Фурье

Определение. Рядом Фурье в вещественной форме, состав-

ленным для периодической функции f (x) с периодом Т, называется тригонометрический ряд

в котором коэффициенты находятся с помощью формул Эйлера – Фурье в вещественной форме:

Определение. Рядом Фурье в комплексной форме, составлен-

ным для периодической функции f (x) с периодом T называется ряд

k=−∞

вкотором коэффициенты находятся с помощью формул Эйлера – Фурье в комплексной форме

Ряд Фурье (5.1) – (5.2) и (5.3) – (5.4) для функции f (x) был построен чисто формально. Возникает вопрос: при каких условиях ряд Фурье сходится к функции f (x)? Соответствующие условия называются условиями Дирихле. Сформулируем их.

Функция f (x) удовлетворяет на отрезке [a, b] условиям Дирихле, если:

14

1) f (x) непрерывна на [a, b] либо имеет на этом отрезке конечное число точек разрыва первого рода;

2) f (x) монотонна на [a, b] либо имеет на этом отрезке конечное число экстремумов.

Таким образом, если функция f (x) удовлетворяет на [a, b]

условиям Дирихле, то этот отрезок можно разбить на конечное число таких отрезков, на каждом из которых f (x) непрерывна и монотонна.

На рис. 5.1 приведен пример кусочно-непрерывной функции.

Рис. 5.1

Теорема Дирихле. Если периодическая с периодом T функция f (x) на отрезке длины T удовлетворяет условиям Дирихле, то:

1)ряд Фурье для этой функции сходится на всей оси Ox ;

2)сумма ряда Фурье равна f (x) во всех точках непрерывности этой функции;

3)в точках разрыва первого рода функции f (x) сумма ряда Фурье равна полусумме левого и правого пределов функции f (x)

вэтих точках.

Отметим, что данная теорема имеет достаточный характер.

6. Разложение в ряд Фурье функции, заданной на отрезке длины Т

Поставим следующую задачу: разложить в ряд Фурье в вещественной форме (формулы (5.1), (5.2)) функцию f (x), заданную

15

на отрезке [α,α + T ] длины T и удовлетворяющую на этом отрезке

условиям Дирихле.

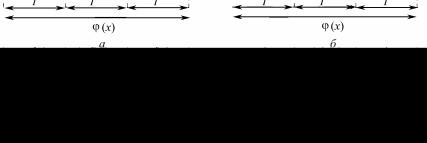
Для решения данной задачи требуется предварительно продолжить периодически f (x) на всю ось Ox . В результате получаем периодическую функцию ϕ( x), совпадающую с f (x) на [α,α + T ]. Соответствующие примеры даны на рис. 6.1.

Рис. 6.1

Итак, функция ϕ( x) – периодическая с периодом T и удовлетворяет условиям Дирихле. Вычислим ее коэффициенты Фурье по формулам (5.2). Учтем при этом, что при x [α,α + T ] имеем

ϕ (x ) ≡ f ( x).

Получаем

зультат (см. по этому поводу свойство 5) периодической функции).

16

Вычислив коэффициенты ak , bk по формулам (6.1), запишем ряд Фурье для функции ϕ( x):

Ряд (6.2) сходится на всей оси Ox к функции j(x) в смысле теоремы Дирихле и, следовательно, к f (x) на [a,a + T ]. Это значит, что во всех внутренних точках отрезка [a,a + T ], в которых функция f (x) непрерывна, сумма ряда (6.2) f (x), а в точках разрыва пер-

вого рода сумма ряда (6.2) равна f ( x − 0) + f (x + 0) .

2

Установим, чему равна сумма ряда (6.2) в концах отрезка [a,a + T ], так как здесь могут иметь место два случая.

Если в точках α и α + T будет f (a) = f (a + T ) (рис. 6.1, а) то все точки вида x = α + nT , где n = 0, ± 1, ± 2, ..., суть точки непрерывности функции j(x) и сумма ряда в этих точках по теореме Дирихле равна f (x).

Если же f (a) ¹ f (a + T ) (рис. 6.1, б), то точки x = α + nT суть точки разрыва первого рода и сумма ряда в этих точках равна

Таким образом, ряд (6.2) с коэффициентами (6.1) на интервале (a,a + T ) имеет своей суммой функцию f (x). На концах этого

в начале данного раздела задача решена.

17

Отметим еще раз, что ряд Фурье для функции f (x), заданный на [α,α + T ], является рядом Фурье для функции ϕ( x), которая по-

лучена из функции f (x) периодическим продолжением ее на всю числовую ось Ox .

Замечание. Отметим, что комплексную форму ряда Фурье для функции f ( x ), заданной на отрезке [α,α + T ] длины T и удовлетворяющую на этом отрезке условиям Дирихле, получаем аналогично, по периодическому продолжению ϕ( x) на основе фор-

мул (5.3) – (5.4). Следовательно, если функция задана на отрезке, то ее разложения в ряд Фурье в вещественной и комплексной формах находятся по формулам (5.1) – (5.4).

7.Приближения функции f(x) отрезками ряда Фурье

Определение. Тригонометрические многочлены

в которых коэффициенты находятся с помощью формул Эйлера – Фурье, в вещественной форме (5.2) называются отрезками ряда Фурье, дающими приближения функции f (x).

Чем выше будет порядок n взятого тригонометрического многочлена Pn ( x) , тем точнее будет приближение функции f (x) отрезком ряда Фурье.

8. Пример решения задачи на разложение в ряд Фурье функции, заданной на отрезке

Пример. Разложить в ряд Фурье в вещественной и комплексной форме функцию y = f (x), заданную графически (рис. 8.1) на

18

отрезке [0,3], и построить ее приближения отрезками ряда Фурье второго и третьего порядка.

и B( x2 , y2 ). Из курса аналитической геометрии известно, что соответствующее уравнение имеет вид

y - y1 = x - x1 . y2 - y1 x2 - x1

В данном случае имеем x1 = 0, y1 = 5; x2 = 3, y2 = 0. Подставляя эти значения в уравнение прямой, получаем

y - 5 = x .

-5 3

Разрешим это уравнение относительно переменной y. Последовательно получаем

19

Теперь вводим функцию j( x) – периодическое продолжение функции f (x) с периодом Т = 3, совпадающую с f (x) на отрезке [0,T ]

(рис. 8.1).

Вычислим коэффициенты вещественной формы ряда Фурье по формулам (5.2), в которых T = 3, w = 2p = 2p (отметим, что

функция f (x) не является ни четной, ни нечетной):

20