введение_в_конфликтологию

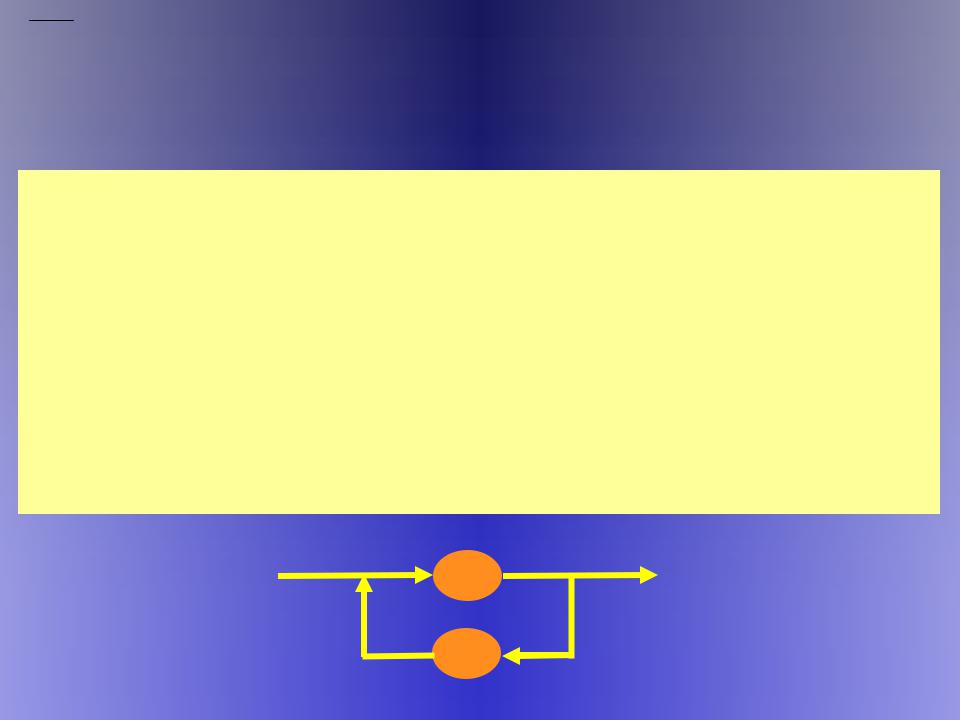
R 1 .

1 ABДинамический метод моделирования и анализа конфликта

Коэффициент обратной связи R

–динамическое сердце системы

Допустим, даны две произвольные системы – А и В такие, что к действию внешних причин на А добавляется обратное действие этой же системы на саму себя, опосредованное положительным или отрицательным действием системы В. Как вычисляется коэффициент обратной связи возникшей петли причинной связи, поясняется на нижеследующем рисунке

Так как система А влияет на систему В, а система В оказывает обратное воздействие на систему А, окончательный результат обратного действия А на саму себя равен произведению действий обеих систем А В = АВ. Динамическое значение фактора АВ выражается конечными рациональными числами, положительными и отрицательными. Для разграничения положительных и отрицательных воздействий системы А на саму себя фактор АВ вычитается из 1 и принимает вид разности (1 АВ). Допуская для простоты, что вес внешних причин, действующих на А, равен 1 и учитывая обратный характер действия разности (1 АВ) на АВ, окончательное выражение имеет следующий вид:

1

R = ---------

1 - АВ

 Динамический метод моделирования и анализа конфликта

Связь стабильности, линейности и хаотичности с конфликтностью

R – параметр (коэффициент обратной связи), управляющий динамикой системы

Вывод: как конфликтные, так и бесконфликтные системы в равной мере могут быть стабильными и нестабильными, линейными и нелинейными, хаотичными и нехаотичными

 Динамический метод моделирования и анализа конфликта

Стабилизирующий синергизм (антагонизм), 0 < R < 1

Синергетическое (антагонистическое) поведение системы динамически линейно. Развитие синергизма (антагонизма) завершается его сохранением на новом – более высоком или более низком уровне стабильного существования системы

Дестабилизирующий синергизм

(антагонизм), R 1 Синергетическое (антагонистическое) поведение системы динамически нестабильно, так как отсутствует предел изменения значений ее переменных (изменение не может остановиться по своей воле), при этом линейно. Развитие синергизма (антагонизма) системы заканчивается для нее катастрофой

 Динамический метод моделирования и анализа конфликта

Пример стабилизирующего синергизма (0 R 1)– доброе слово,

увеличивающее симпатию; поощрение, стимулирующее работу и т. п.

КУКУШКА И ПЕТУХ

«Как, милый Петушок, поешь, ты громко, важно!»- «А ты, Кукушечка, мой свет,

Как тянешь плавно и протяжно:

Во всем лесу у нас такой певицы нет!» - «Тебя, мой куманек, век слушать я готова».- «А ты, красавица, божусь, Лишь только замолчишь, то жду я, не дождусь, Чтоб начала ты снова...

Отколь такой берется голосок? И чист, и нежен, и высок!..

Да вы уж родом так: собою невелички, А песни, что твой соловей!» - «Спасибо, кум; зато, по совести моей, Поешь ты лучше райской птички, На всех ссылаюсь в этом я»

Тут Воробей, случась, примолвил им: "Друзья! Хоть вы охрипните, хваля друг дружку, - Все ваша музыка плоха!.." За что же, не боясь греха, Кукушка хвалит Петуха? За то, что хвалит он Кукушку.

Динамический метод моделирования и анализа конфликта

Пример дестабилизирующего (саморазрушающегося)

синергизма (R 1) – принудительное застолье по И. А. Крылову

ДЕМЬЯНОВА УХА

"Соседушка, мой свет! Пожалуйста, покушай". -

"Соседушка, я сыт по горло". - "Нужды нет, Еще тарелочку; послушай:

Ушица, ей-же-ей, на славу сварена!" - "Я три тарелки съел". - "И полно, что за счеты:

Лишь стало бы охоты, - А то во здравье: ешь до дна!

Что за уха! Да как жирна; Как будто янтарем подернулась она.

Потешь же, миленький дружочек!

Вот лещик, потроха, вот стерляди кусочек! Еще хоть ложечку! Да кланяйся, жена!" Так потчевал сосед Демьян соседа Фоку

Ине давал ему ни отдыху, ни сроку; А с Фоки уж давно катился градом пот. Однако же еще тарелку он берет, Сбирается с последней силой

И- очищает всю. " Вот друга я люблю! - Вскричал Демьян. - Зато уж чванных не терплю. Ну, скушай же еще тарелочку, мой милый! “ Тут бедный Фока мой, Как ни любил уху, но от беды такой, Схватя в охапку Кушак и шапку,

Скорей без памяти домой -

Ис той поры к Демьяну ни ногой.

Динамический метод моделирования и анализа конфликта

Пример стабилизирующего антагонизма (0 R 1) –

соперничество, увеличивающее разнообразие элементов и качество функционирования системы

Динамический метод моделирования и анализа конфликта

Пример дестабилизирующего антагонизма (R 1) –

соперничество, приводящее к уничтожению (гибели) одного или обоих антагонистов

 Динамический метод моделирования и анализа конфликта

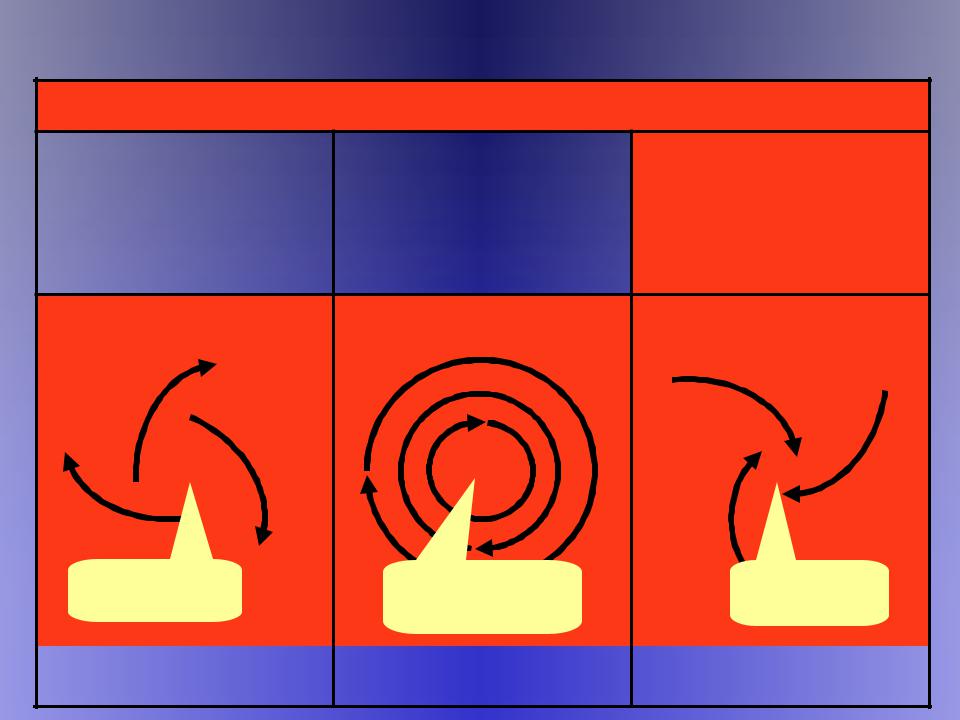
Динамическая классификация конфликтов

Конфликтырегуляторы ( 1 R 0)

Конфликтное поведение системы динамически стабильно и линейно. Развитие конфликта завершается его сохранением на новом – более высоком или более низком уровне стабильного существования системы

Конфликты-пульсации (R = 1)

Конфликтное поведение системы нестабильно, но линейно. Развитие конфликта происходит в виде регулярно и с постоянной амплитудой повторяющегося процесса

Конфликты-катастрофы (R 1)

Конфликтное поведение системы динамически нестабильно (хаотично). Развитие конфликта носит катастрофический для системы характер

 Динамический метод моделирования и анализа конфликта

Динамическая классификация конфликтов

 Динамический метод моделирования и анализа конфликта

Конфликт-регулятор ( 1 R 0 )

Внешнее воздействие вызывает конечный по продолжительности дрейф в сторону нового (более высокого, если внешний импульс отрицательный, и более низкого, если импульс положительный) уровня динамически стабильного существования

С течением времени и при прочих равных обстоятельствах система, находящаяся в состоянии стабилизирующего конфликта, монотонно увеличивает свою конфликтность, не доводя себя до саморазрушения