Тема 10. Планарные графы. Грани. Формула Эйлера. Полный граф. Двудольный граф. Полный двудольный граф. Необходимые и достаточные условия планарности.

Рассмотрим теперь вопрос, связанный с интерпретацией графов как диаграмм на плоскости. С иллюстративной точки зрения неважно, как именно на плоскости рисунка расположены вершины и рёбра – в линию, по окружности, хаотично. Лишь бы они отражали отношение смежности.

Но есть задачи, где само расположение узлов и рёбер имеет принципиальное значение: электрические схемы, инженерные коммуникации и т.п. Здесь мы кратко рассмотрим только возможность изобразить граф на плоскости без пересечений рёбер.

Граф, который может быть изображен на плоскости без пересечений рёбер, называется планарным графом.

Например, граф

G({a, b, c, d},{{a, b}{a, c}{a, d}{b, c}{b, d}{c, d}})

можно изобразить и с пересечением и без пересечений рёбер, поэтому этот граф является планарным.

А вот граф, представленный следующей диаграммой, планарным не является.

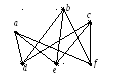
Для того, чтобы выяснить, при каких условиях граф является планарным, потребуется ввести еще несколько понятий.

Если граф планарный и изображен на плоскости без пересечений рёбер, то диаграмма для графа разделяет плоскость на части, называемые гранями.Грань – максимальный участок плоскости, в котором две точки могут быть соединены линией (любой формы), не пересекающей ребро графа.

На рисунке три грани изображены треугольниками: 1 – abc, 2 – abd, 3 – bcd. Грань4представляет собой внешнюю область плоскости.

Каждая грань соответствует циклическому маршруту в графе.

В примере грани 2соответствует циклabda.

Если связный граф является планарным и изображен на плоскости без пересечений рёбер, то число граней может быть найдено по известному числу вершин и рёбер. Формула, выражающая число граней через число вершин и рёбер известна какформула Эйлера. Она справедлива также и для мультиграфов и для графов с петлями.

Обозначим

число вершин – символом v,

число рёбер – символом e,

число граней – символом f(от англ. “face”)

Формула Эйлера:ve+f=2

Интересно отметить, что эта формула может быть доказана по индукции по числу рёбер графа.

База индукции:

Связный граф без рёбер представляет единственную вершину степени 0. Есть только одна грань – вся плоскость: v=1,e=0,f=1 ve+f=2.

Индукционное предположение: ve+f=2 для некоторого графа сeрёбрами.

Индукционный переход:

Добавим к графу ребро. Есть два способа:

1. Добавляемое ребро инцидентно одной вершине исходного графа и новой добавленной вершине. Такое добавление не образует цикла и не меняет числа граней. Соотношение сохраняется. v′=v+1,e′=e+1,f′=f v′e′+f′=2.

2. Добавляемое ребро инцидентно двум вершинам исходного графа (или, возможно, петля в графе с петлями). Число вершин не меняется: v′=v,e′=e+1. При этом обязательно образуется цикл и грань:f′=f+1 v′e′+f′=2. (В графе с петлями петля тоже грань).

Граф называется полным, если все его вершины попарно смежные.

Так как в простом графе все ребра двухэлементные (нет петель) это можно записать так:

Е={{x, y} | xV & yV}∖{{x} |xV}

Полный граф с nвершинами (точнее класс графов, изоморфных такому графу) обозначается обычноK_n.

Примеры

Заметьте, что граф K₄является планарным, а графK₅– нет.

Граф называется двудольным, если его множество вершин можно представить в виде объединения двух непересекающихся множеств и при этом никакие две вершины одного множества не являются смежными.

V=AB & AB= & (xA & yA  {x, y}E)  & (xB & yB  {x, y}E)

Двудольный граф называется полным двудольным, если любые два элемента разных множеств (долей) являются смежными.

 xA xB {x, y}E

Если |A|=mи |B|=nто полный двудольный граф (класс эквивалентности по изоморфизму) обозначаетсяK_m,n.

Примеры.

Граф K_2,3является планарным, а графK_3,3не является.

Теперь рассмотрим следующие утверждения:

В простом планарном графе каждая грань ограничивается, по крайней мере, тремя рёбрами.

Каждое ребро ограничивает не более двух граней.

Необходимое условие планарности.

Комбинируя их (3f≤2e) с формулой Эйлера (ve+f=2), получаем, чтов простом связном планарном графе с более, чем тремя вершинами (v>3) не более 3v6 рёбер.

e≤3v6

Данное условие планарности простого графа связывает только число вершин и рёбер. Используя его можно доказать непланарность графов K₅иK_3,3. С его помощью можно доказывать непланарность и других графов.

( e≤3v6)граф не планарный

Но это условие не является достаточным для планарности.

Необходимое и достаточное условие устанавливается теоремой Куратовского (доказательство можно посмотреть в специальной литературе):

Граф является планарным тогда и только тогда, когда он не содержит в качестве подграфов ниK₅ ни K_3,3.