вектора E на касательную плоскость в этой точке равны нулю, то есть вектор E направлен по нормали к эквипотенциальной по-

верхности. Поскольку вектор E сам направлен по касательной к соответствующей силовой линии электрического поля, можно заключить, что силовые линии поля пронизывают эквипотенциальные поверхности в каждой точке перпендикулярно соответствующим касательным плоскостям. Таким образом, силовые линии электрического поля в каждой точке эквипотенциальной поверхности параллельны направлению нормали к поверхности.

3.2. Теорема Гаусса. Вычисление полей. Энергия электрического поля

3.2.1. Теорема Гаусса

Заряженные макроскопические тела содержат большое количество элементарных зарядов, распределенных на их поверхности либо в объеме. Для того, чтобы рассчитать электрические поля, создаваемые в пространстве заряженными телами, нужно просуммировать напряженности всех полей, создаваемых отдельными точечными зарядами. Это очень сложная, а часто и невыполнимая задача.

Поэтому, вместо того, чтобы суммировать напряженности отдельных зарядов, можно просуммировать все векторы напряженности результирующего поля, входящие и выходящие из объема, занятого зарядами. Поскольку векторы напряженности являются касательными к силовым линиям поля, для этого нужно просто сосчитать число входящих и выходящих силовых линий.

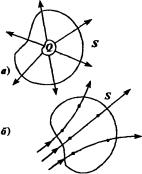
Возьмем некоторый объем, занятый зарядами, суммарное число которых Q, и заключим его внутрь воображаемой замкнутой поверхности S (рис.). Если заряд равен нулю, поле отсутствует. Если заряд находится вне поверхности, си-

134

ловые линии пронизывают поверхность. Однако полное число силовых линий, проходящих сквозь поверхность, равно нулю (число входящих линий равно числу выходящих). При наличии же внутри поверхности отличного от нуля заряда суммарное число силовых линий будет отлично от нуля. Очевидно, их число должно быть пропорционально величине заряда Q. Именно в этом состоит содержание теоремы Гаусса, связывающей число силовых линий, проходящих через поверхность, охватывающую систему зарядов, с числом этих зарядов.

Для того чтобы придать теореме Гаусса формальное выражение, определим понятие потока вектора через поверхность.

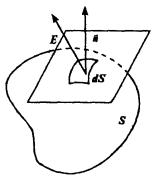
Выделим на поверхности S бесконечно малый элемент площади dS и обозначим единичный вектор нормали к касательной плоскости n (рис.). По-

током вектора E через элемент поверхности dS будем называть скалярную величину

Удобно ввести формальное обозначение векторного элемента площади dS = ndS , тогда формула (3.15) запишется в виде:

Величину полного потока вектора через поверхность можно получить, просуммировав выражение (3.16) по всем элементам

S

Вычислим, например, поток вектора через поверхность сферы, окружающей точечный заряд. В этом случае величина потока

где R — радиус сферы, охватывающей заряд.

135

В случае точечного заряда направление радиуса-вектора r совпадает с направлением нормали к поверхности сферы в точке по-

верхности. Поэтому (er nr ) = 1. Отсюда:

Для постоянной k принято пользоваться обозначением

k = 4πε1 0 смысл которого выяснится позже. Используя это обозна-

чение, получим для потока вектора напряженности через поверхность сферы, окружающей точечный заряд,

Это и есть теорема Гаусса в интегральной форме. Она справедлива для произвольной системы электрических зарядов, и в этом случае утверждает, что поток вектора напряженности через произвольную замкнутую поверхность, внутри которой находится система зарядов, равен суммарному заряду, деленному на константу

ε0.

Теорема Гаусса позволяет довольно просто находить напряженности полей макроскопических тел. Определим, например, напряженность поля бесконечной однородно заряженной плоскости (рис.). Рассмотрим для определенности положительно заряженную бесконечную

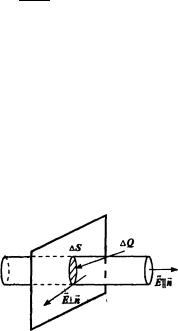
плоскость. Из соображений симметрий следует, что результирующее электрическое поле такой плоскости также однородно, а линии напряженности будут перпендикулярны плоскости и направлены вовне. Выберем на плоскости элемент площади S, содержащий электрический заряд Q. Поверхностью, содержащей внутри себя заряд Q выберем цилиндр сечением S. Вектор E параллелен оси цилиндра и перпендикулярен его основаниям. Поток вектора E будет равен:

136

E взаимно перпендикулярны, первый интеграл в правой части формулы тождественно равен нулю. Второй член равен

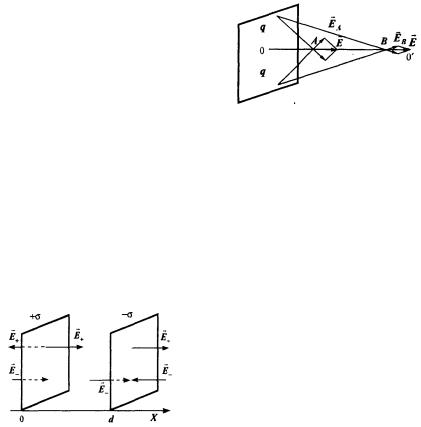
плоскости не убывает с расстоянием, хотя поле каждого отдельного заряда убывает по закону Кулона. Почему это происходит, видно из рис. Рассмотрим поле на оси ОO'. Оно складывается в каждой точке векторным образом из напряженностей полей отдельных точечных зарядов. Для каждого заряда на плоскости найдется равный ему симметричный заряд, и в результате поле будет направлено по указанной оси. Далее из рис. видно, что, хотя поле EA по величине превышает поле EB (точка А находится на меньшем расстоянии от источника поля, чем точка В), угол наклона вектора EA к оси больше, чем угол наклона EB, и поэтому результирующее поле оказывается одинаковым, равным (3.23).

Важный случай представляет собой поле двух разноименно заряженных плоскостей (рис.). Поскольку поле каждой плоскости одинаково во всем пространстве, а результирующее поле представляет собой

137

векторную сумму полей каждой плоскости E = E+ + E–, видно, что в пространстве слева и справа от плоскостей E = 0, в то время как в объеме между плоскостями

Система разноименно заряженных плоскостей представляет собой плоский конденсатор. Таким образом, в плоском конденсаторе электрическое поле сосредоточено в пространстве между его обкладками. Конденсатор является своеобразным накопителем электрического поля.

Рассмотрим, как изменяется потенциал поля плоского конденсатора. Так как электрическое поле плоского конденсатора однородно в вертикальной плоскости (см. рис.), то потенциал в пространстве между заряженными плоскостями изменяется только в направлении оси X. Соотношение (3.14) в этом случае приобретает вид

Найдем разность потенциалов внутри конденсатора, учитывая, что напряженность поля сохраняет постоянное значение (3.25),

0

Таким образом, эквипотенциальные поверхности плоского конденсатора представляют собой плоскости, параллельные обкладкам. Полная разность потенциалов в конденсаторе с расстоянием между пластинами равным d,

Пусть площадь однородно заряженной пластины S, а ее заряд

Q. Тогда поверхностная плотность заряда σ = Q/S. Используя это соотношение и (3.24) получим связь между зарядом конденсатора и создаваемой им разностью потенциалов:

138