Luciv / МКОИ_пособие

отражения рассчитывается относительно идеального отражающего рассеивателя.

Идеальный отражающий рассеиватель (Perfect Reflecting Diffuser) - это теоретическая поверхность, которая одновременно является и идеально отражающей (коэффициент отражения равен 100%), и идеально ламбертовской (энергетическая яркость одинакова по всем направлениям). Поэтому коэффициент отражения определяется как отношение энергии, отраженной от образца, к энергии, которая была бы отражена идеальным отражающим рассеивателем (ИОР), освещенным и рассматриваемым при идентичной геометрии. При использовании фотометрического шара коэффициент полного отражения равен отражательной способности, а при двунаправленных вариантах геометрии коэффициент отражения, измеренный относительно ИОР по 0-1-шкале, лишь подобен коэффициенту полного отражения.

Поскольку ИОР физически не существует, национальными лабораториями по стандартизации (такими, как Национальный институт по стандартизации и технологии в США - NIST), а также производителями измерительных приборов выполнены стандартные эталоны, которые калиброваны относительно теоретической мишени - ИОР.

1.4.7Ответ ЗС человека

Спектральное измерение (или стандартизация) источников света и материалов обеспечивает необходимую для колориметрии физическую информацию, но дело прогнозирования ответа ЗС человека остается за количественными методами оценки этой информации.

Следуя определению базовой колориметрии, данному Вышецким (1973), количественное описание ответа ЗС человека через психофизику цветовых соответствий сосредоточено на первичном уровне зрения (то есть на уровне поглощения энергии колбочковыми фоторецепторами). Являясь базисом колориметрии, возможность прогнозировать, будут ли два стимула визуально соответствовать друг другу для усредненного наблюдателя, полезна в различных сферах своего применения. Несмотря на то, что эта система не описывает цветовое восприятие как таковое, она создает фундамент для его описания и позволяет прогнозировать соответствия (что востребовано в разных сферах деятельности), а также обеспечивает необходимый промышленный инструментарий для установки допусков на эти соответствия.

Способность ЗС человека к выявлению цветовых соответствий определяется спектральной чувствительностью трех типов колбочек. После поглощения энергии колбочками информация о спектральном происхождении сигнала утрачивается. Если сигналы от колбочек трех типов в ответ на два стимула одинаковы, то эти стимулы неизбежно будут соответствовать друг другу по цвету, когда просматриваются в одинаковых условиях, то есть, когда в ЗС не попадает никакой лишней информации, приводящей к возникновению визуальных отличий. Таким

41

образом, если известны спектральные чувствительности трех типов колбочек, то два стимула с известными спектральными распределениями

энергии Φ1(λ ) и Φ2 (λ ) будут соответствовать друг другу по цвету. В случае если спектральное распределение энергии этих стимулов и каждая из трех

колбочковых чувствительностей - L(λ ), M (λ ) и S (λ ), проинтегрированные по длинам волн, - равны. Данное равенство проиллюстрировано уравнениями 1.1: два стимула соответствуют друг другу по цвету, если выполняются все

три равенства:

∫ Φ1(λ )L(λ )dλ = ∫ Φ 2 (λ )L(λ )dλ

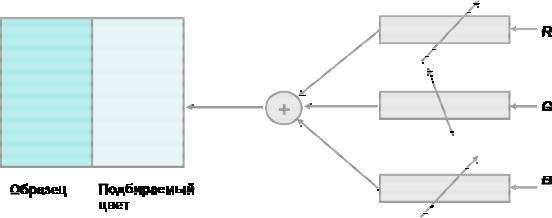
Уравнения 1.1 иллюстрируют определение метамеризма. Поскольку для достижения цветового соответствия равными между собой должны быть все соответствующие пары интегралов, то нет необходимости в том, чтобы спектральные распределения энергии стимулов были бы равны между собой по каждой из длин волн. Этот принцип положен в основу аддитивного смешения цветов, проиллюстрированный на рис. 1.15.

Рисунок 1.15 Сложение цветовых стимулов

Цветовые соответствия описаны как количества трех аддитивных первичных световых потоков, необходимых для достижения визуального соответствия тестовому стимулу. Наличие коэффициентов kR , kG , kB указывает на то, что при различных наборах кардинальных стимулов понадобятся различные количества этих кардинальных стимулов.

Коэффициенты kR , kG , kB указывают на необходимые количества первичных стимулов и называются «трехстимульными значениями».

Таким образом, любой цвет может быть визуально уравнен точными количествами трех первичных стимулов, и, следовательно, эти количества (трехстимульные значения), в совокупности с характеристиками самого набора первичных стимулов, позволяют специфицировать цвет. Если у двух

42

стимулов одинаковые трехстимульные значения - это означает, что они будут визуально соответствовать друг другу в одинаковых условиях просмотра. В соответствии со схемой на рис. 1.15 сложение цветовых стимулов осуществляется в соответствии с формулами:

C+ k R R = kGG + kB B .

1.4.8Законы Грассмана

Воснову вычислений в колориметрии положены законы Грассмана, справедливые для случая аддитивного смешения цветов [8].

1-ый закон Грассмана гласит:

Цвета ведут себя в смесях независимо от их спектрального состава. Этот закон позволяет оперировать не излучениями, а цветами.

2-ой закон Грассмана – закон об аддитивности цветов: цвета можно складывать, то есть если верны два или более утверждений U=V, W=X, то верно и третье: (U+W)=(V+X).

Следствие этого - пропорциональность: U=V <=> tU=tV

3-ий закон Грассмана: цвет представляет собой аффинный трехмерный вектор, и все цвета преобразуются по законам векторной алгебры.

Встрогой математичекой формулировке 3-ий закон гласит: между любыми 4 цветами всегда существует линейная зависимость, хотя существует неограниченное число линейно независимых совокупностей из трех цветов: C=rR+gG+bB.

C учетом 2-го закона, eсли C=rR+gG+bB, то kC=krR+kgG+kbB.

Цвета обладают свойствами симметрии: U=V <=>V=U;

транзитивности: U=V и V=W => U=W.

Законы эти справедливы настолько, насколько справедливы любые законы, описывающие биологические системы.

1.4.9Удельные координаты цвета

После принятия МКО в 1924 г. функции световой эффективности V (λ) внимание было сосредоточено на развитии колориметрической системы, задачей которой являлось описание метамерных стимулов, соответствующих друг другу по цвету при восприятии их усредненным наблюдателем.

Удельные координаты цвета (или спектральные трехстимульные значения) ( r (λ), g (λ), b (λ) ) были получены путем визуального сравнения спектрально чистых стимулов по каждой длине волны с аддитивной смесью трех основных стимулов при одинаковой энергетической яркости без какойлибо световой адаптации зрения. Следовательно, трехстимульные значения - это цветовые координаты стимула при темновой адаптации наблюдателя.

43

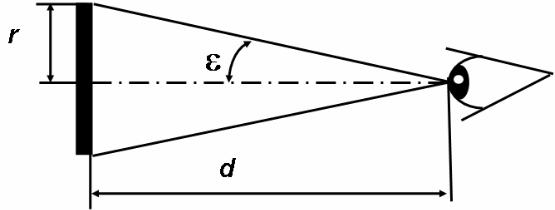
Стандартный колориметрический наблюдатель МКО 1931 был экспериментально получен с использованием 2°-го поля зрения. Поле зрения определяется в соответствии с уравнением (рис. 1.16):

α = 2ε = 2arctg (r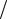d )

Рисунок 1.16 Поле зрения

Последнее означает, что уравниваемые стимулы попадали на сетчатку наблюдателя исключительно в пределах ее центральной ямки. Функции сложения цветов для 2° были получены Райтом и Гилдом, их называют двухградусными функциями сложения цветов или кратко двухградусным наблюдателем.

В пятидесятых годах прошлого века Стайлс и Берг (1959) провели эксперименты и собрали данные для функций сложения цветов при большем поле зрения. Необходимость такой работы была продиктована несоответствием между колориметрическим и визуальным определением белизны бумаги. Эксперименты были выполнены с использованием 10°-го поля зрения, выходящего за пределы центральной ямки сетчатки, благодаря чему из функций цветового соответствия было исключено влияние поглощения в желтом пятне. Оказалось, что данные по большим полям существенно отличаются от двухградусных, в результате чего был принят т.н. дополнительный стандартный колориметрический наблюдатель МКО 1964, иногда называемый десятиградусным наблюдателем.

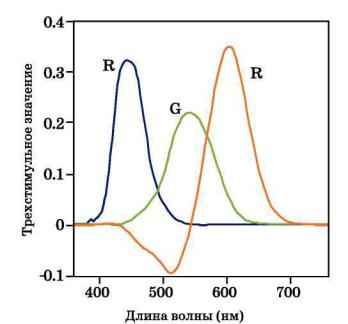
На рис. 1.17 показан набор спектральных трехстимульных значений для монохроматических основных стимулов с длинами волн 435,8 (B); 546,1 (G); и 700.0 нм (R). Совокупность спектральных трехстимульных значений для полного спектра называют функциями сложения цветов.

Отметим, что некоторые из спектральных трехстимульных значений на рис. 1.16 отрицательны, что подразумевает участие в сравнении отрицательных количеств энергии, например, отрицательное значение основного R- стимула необходимо для уравнивания монохроматического стимула с длиной волны 500 нм. Так происходит потому, что узкополосные стимулы слишком насыщенны, чтобы быть уравненными основными

44

стимулами (то есть они лежат вне цветового охвата тройки основных стимулов).

Рис. 1.17 Спектральные трехстимульные значения для колориметрической системы МКО RGB с монохроматическими основными стимулами 435.8, 546.1 и 700.0 нм.

Ясно, что отрицательное количество света добавить невозможно, поэтому отрицательные трехстимульные значения были получены добавкой того или иного основного стимула к монохроматическому (исследуемому) свету для понижения насыщенности последнего и компрессии его в цветовой охват тройки основных стимулов. Таким образом, монохроматический стимул с длиной волны 500 нм, смешанный с определенным количеством основного R стимула, оказывается уравненным с аддитивной смесью соответствующих количеств основных стимулов G и B. Функции сложения цветов, показанные на рис. 1.18=6, демонстрируют значения основных стимулов, необходимые для уравнивания с монохроматическими стимулами каждой из длин волн видимого спектра.

Полагая, что спектральное распределение энергии любого произвольно взятого стимула - это аддитивная смесь различных количеств монохроматических стимулов, трехстимульные значения данного стимула можно получить умножением функций сложения цветов на величину энергии исследуемого стимула по каждой из длин волн (закон пропорциональности Грассмана) с последующим интегрированием результатов умножения (закон аддитивности Грассмана). Таким образом, общие формулы для вычисления трехстимульных значений стимула со спектральным распределением энергии Ф( λ ) представляют собой формулы 1.3-1.5:

λ

45

Затем МКО решила выполнить преобразование полученных функций сложения цветов к функциям для еще одного набора основных стимулов – XYZ. Основной предпосылкой к этому преобразованию было стремление устранить отрицательные значения из функций сложения цветов и принудительно уравнять одну из этих функций с функцией фотопической световой эффективности V( λ ) МКО 1924.

Отрицательные значения были удалены за счет создания такого набора основных стимулов, с помощью которого можно было бы уравнять все физически воспроизводимые цветовые стимулы. Такими основными стимулами оказались лишь воображаемые основные стимулы, более насыщенные, чем монохроматический свет, и их получение - это математическая абстракция. Нужно отметить, что, несмотря на то, что основные стимулы условны, функции сложения весов, полученные с такими основными стимулами, основаны на совершенно реальных результатах цветового уравнивания и подчиняются законам Грассмана.

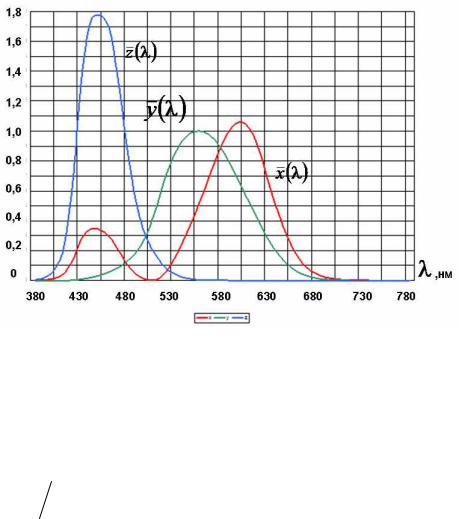
Принудительное уравнивание одной из функций сложения цветов с функцией V( λ ) выполнено с целью внедрения фотометрической системы МКО (принята в 1924 г.) в колориметрическую систему МКО (принята в 1931 г.). Поступили так: воображаемым основным стимулам X и Z был адресован сугубо «неяркостный» ответ, а вся полнота яркостного ответа адресована стимулу Y. Функции сложения весов для основных стимулов XYZ – это соответственно, которые именуются как «удельные координаты цвета стандартного колориметрического наблюдателя МКО 1931». Графическое представление этих функций приведено на рис. 1.18 в диапазоне длин волн 380-780 нм.

Трехстимульные значения цветовых стимулов XYZ вычисляются аналогично трехстимульным значениям RGB (1.3-1.5):

коэффициент.

Спектральное распределение энергии определяется по-разному: для самосветящихся стимулов (например, источники света и ЖК-дисплеи) Ф( λ ) - это обычная спектральная энергетическая яркость (относительное спектральное распределение энергии); для отражающих материалов Ф( λ ) -

46

это произведение спектрального коэффициента отражения R( λ ) и относительного спектрального распределения энергии S( λ ) интересующего источника света или осветителя, то есть R( λ )S( λ ); для пропускающих материалов Ф( λ ) - это произведение спектрального коэффициента пропускания материала Т( λ ) и относительного спектрального распределения энергии S( λ ) интересующего источника света или осветителя, то есть T( λ )S( λ ).

Рис. 1.18 Спектральные трехстимульные значения стандратного колориметрического наблюдателя МКО 1931.

Нормирующий коэффициент k в формулах 1.6-1.8 по-разному определен для т.н. абсолютной и относительной колориметрии.

Вабсолютной колориметрии k равен 683 лм/Вт, что обеспечивает совместимость колориметрической системы с фотометрической.

Вотносительной колориметрии k определен уравнением 1.9:

В относительной колориметрии нормировка по формуле 1.9 ведет к тому, что трехстимульные значения шкалируются в диапазон от 0 до примерно 100 для различных материалов, и следует отметить, что, когда относительная колориметрия используется для вычисления трехстимульных значений источника света, - трехстимульное значение Y всегда равно 100.

Подобно функции V (λ), каждая из функций цветового соответствия МКО XYZ представляет собой линейную комбинацию колбочковых ответов, поэтому взаимоотношения между функциями сложения цветов XYZ и колбочковыми ответами определены линейными ЗхЗ-матричными преобразованиями (3x3).

47

Таким образом, требуемые основные стимулы, оставаясь лишь воображаемыми, создают функции сложения весов только с положительными значениями.

1.4.10 Цветовое пространство XYZ. График цветности

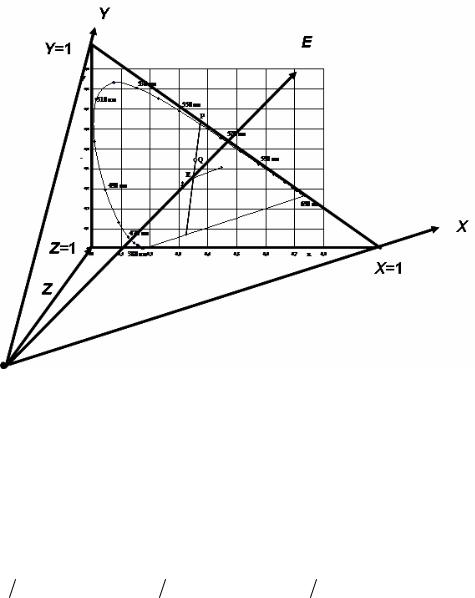
На рис. 1.19 изображено трехкоординатное цветовое пространство, определяемое основными цветами XYZ. Единичная плоскость этого пространства X+Y+Z=1 называется графиком цветности МКО 1931 г. Вершины цветового треугольника соответствуют точкам пересечения основных спектральных цветов с единичной плоскостью и имеют координаты (x,y): X(1,0); Y(0,1); Z(0,0).

Рисунок 1.19 Цветовое пространство XYZ

МКО разработаны специальные графики цветности (x,y) для получения удобного двумерного представления цветов. Преобразование трехстимульных значений в координаты цветности выполняется через нормировку, удаляющую информацию о яркости; данное преобразование - это т.н. перспективная одноточечная проекция точечных данных трехмерного трехстимульного пространства на единичную плоскость этого пространства (с центром проекции в точке начала координат), как показано в уравнениях 1.10:

Поскольку (x+y+z=1), для описания координат цветности достаточно двумерной функции. Третью координату цветности всегда можно получить из двух других: z=1-x-y. График цветности представлен на рис. 1.20.

Координаты цветности не содержат сведений о цветовом восприятии стимулов, поскольку не несут в себе информации о яркости стимула

48

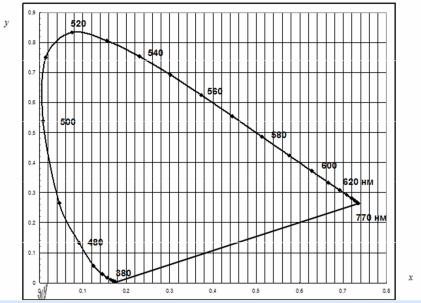
(следовательно, о его светлоте) и не учитывают эффект хроматической адаптации. При изменении вида адаптации наблюдателя цвет, которому соответствует данный набор координат цветности, восприятие цвета может существенно измениться. Например, цвет может измениться от желтого, при адаптации к дневному свету, до синего, при адаптации к свету ламп накаливания.

Рисунок 1.20 График цветности (x,y) МКО 1931 г. с локусом цветности и прямой линией пурпурных цветов

Масса усилий затрачена на попытки создания диаграммы цветностей, которая была бы равномерной по восприятию. Это соответствует преобразованию номинальной шкалы в интервальную, что вообще говоря, невозможно.

1.4.11 Равномерные цветовые пространства

Мы рассматривали равномерные цветовые пространства CIELAB и CIELUV [1]. Эти пространства используют трехмерные пространства, в которых оси приблизительно коррелируют с восприятием светлоты, насыщенности и цветового тона стимула. Достичь такого результата удалось за счет учета хроматической адаптации и нелинейности зрительных ответов, но главная цель создания упомянутых пространств - это разработка методов равномерного измерения цветовых отличий, что не может быть выполнено корректно с помощью трехстимульных пространств или диаграмм цветности.

В 1976 г. к использованию были рекомендованы оба упомянутых пространства. Вышецкий (1986) дает обзор развития цветовых пространств МКО.

49