Luciv / МКОИ_пособие

(1.36)

где ϕ rg , ϕ gb , ϕ br - углы между векторами откликов в метрическом векторном пространстве A r , A g , Ab (в соответствии с рис. 1.21);

AW AYe− B A Pr−G .

Цветовая яркость Lc = Ac2 может быть выражена через цветовые

Белому равноэнергетическому цвету в метрическом векторном цветовом пространстве соответствует вектор белого AW . Плоскость цветности перпендикулярна вектору равноэнергетического белого AW .

Насыщенность цвета в метрическом векторном пространстве количественно определяется косинусом угла между вектором данного цвета и вектором равноэнергетического белого цвета:

Рисунок 1.21 Представление цветов в метрическом векторном пространстве.

Цветовой тон определяется углом ϕH в плоскости цветности между

где m=0, n=0 для 1-го квадранта, m=0, n=1 для 2-го квадранта, m=1, n=1 для 3-го квадранта, m=1, n=2 для 4-го квадранта.

Ach == AYe2 − B + APr2 −G .

51

Ожидается, что построение ТВ систем на принципе постоянной цветовой яркости позволит приблизить воспроизведение цветных изображений к фотометрически точным условиям цветопередачи, повысить четкость на цветных деталях изображений, в том числе в насыщенных цветах, приблизив ее к четкости черно-белых изображений. Эта теория находится в развитии. Проблема состоит в определении основных величин. В колориметрии цвет численно определяется через функции относительного спектрального распределения реакций глаза, обусловленных работой колбочек, в неметрическом векторном пространстве. Предлагаемое метрическое векторное цветовое пространство позволит определить цветовую фотометрию, основанную на откликах цветовых зрительных каналов. Это пространство равномерно и в нем определены скалярные умножения. Основным законом цветовой фотометрии является аддитивность векторов. Предложена модель цветового зрения. Показано, что цветовые отклики могут быть описаны векторами в метрическом пространстве. В соответствии с предложенной моделью, основными величинами цветовой фотометрии являются амплитуды цветовых реакций и углы между векторами цветов. Гетерохромная яркость зависит от амплитуды хроматического отклика, а тон и насыщенность цвета зависят от углов.

Выводы

В разделе рассмотрены основные принципы базовой колориметрии. Однако, несмотря на то, что описанные методы давно устоялись и успешно применяются на протяжении десятилетий, для расширения базовой колориметрии до уровня эффективной спецификации цветового восприятия стимулов в широком диапазоне условий просмотра, необходимо дополнить учитываемые компоненты как минимум, данными, описывающими: статус хроматической адаптации; статус световой адаптации; уровень фотометрической яркости; цвет фона; цвет окружения и др.

Дальнейшее развитие колориметрии связано с разработкой цветовой фотометрии, в которой цветовая модель создается не в аффинном, а в метрическом векторном пространстве.

2Методы сегментации изображений

2.1Методы математической статистики

В этом разделе мы кратко рассмотрим методы математической статистики, знание которых необходимо при рассмотрении признаков объектов и проведении обработки данных выполненных экспериментальных исследований [12].

2.1.1 Распределение дискретной случайной величины

Распределением дискретной случайной величины x является вероятность появления всех возможных значений случайной величины, то есть p(xi ) = P(x = xi ), i=1,2,...

52

Интегральная функция распределения определяет вероятность того, что случайная величина x ≤ xi :

F (xi ) = P(x ≤ xi ) = ∑ p(xi ).(2.1) x≤ xi

Из (2.1) следует: 0 ≤ F (xi ) ≤ 1 для всех xi ; F (xi ) ≥ F (x j ) для всех xi ≥ x j ;

∑ p(xi ) = 1. i

На рис. 2.1 представлена гистограмма яркостей изображения, которая является примером функции распределения значений яркости в изображении.

Рисунок 2.1 Функция распределения яркости в изображении

2.1.2 Параметры, характеризующие центр распределения

Характеристика распределения, определяющая значение, вокруг которого группируется распределение, может быть определена как среднее значение, медиана или мода распределения.

Среднее значение, или математическое ожидание функции распределения определяется в соответствии с уравнением:

изображении, C( fi )-число отсчетов в изображении, имеющих значение fi .

53

Медиана равна тому значению непрерывной случайной величины, которое делит площадь под кривой плотности распределения пополам. Для дискретной случайной величины точное равенство может быть достигнуто только в частном случае. Для оценки медианы функции распределения случайной величины от 0 до некоторого значения xk , для которого выполняется условие:

k

∑ p(xi ) = 0,5 . i =0

В этом случае медиана равна: xmed = xk .

Мода – это значение случайной величины, имеющей максимальную вероятность. Мода равна значению, соответствующему максимуму функции распределения.

На рис. 2.2 представлена гистограмма распределения, и показаны положения среднего значения x =129 (белый визир), медианы xmed (красный визир) и две белые стрелки, указывающие положения распределения xmod1 = 121 и xmod2 = 181.

Рисунок 2.2 Параметры распределения.

2.1.3Моменты распределения

Распределение является полностью заданным, если известны все его моменты. На практике для характеристики распределения во многих случаях достаточно иметь оценки не более 4 моментов распределения.

Момент распределения вычисляется в соответствии с формулой:

k = E(x)k = ∑ (xi )k p(xi ).

i

k -ый момент относительно математического ожидания называется k - ым центральным моментом и вычисляется в соответствии с:

54

Корень квадратный из дисперсии называется средним квадратическим отклонением (СКО) и обозначается символом σ :

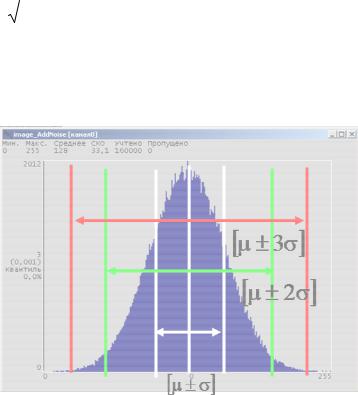
99,7%, как показано на рис. 2.3.

Рисунок 2.3 Нормальный закон распределения случайной величины

Если закон распределения отличается от нормального, то число отсчетов в интервале µ1' ± kσ определяется в соответствии с:

[1 − (1k 2 )]×100%

Третий центральный момент вычисляется в соответствии с уравнением:

55

Если распределение унимодальное, то при µ3 < 0 оно имеет левостороннюю асимметрию, если µ3 > 0 , то распределение имеет правостороннюю асимметрию (рис. 2.4), иначе распределение симметрично.

Рисунок 2.4 Правосторонняя асимметрия распределения

Чтобы сравнивать два распределения с разными моментами в качестве оценки асимметрии вычисляется нормированный коэффициент асимметрии как отношение асимметрии распределения к мере рассеяния:

Четвертый центральный момент связан с островершинностью и вычисляется в соответствии с:

µ4 = E(x −µ′1)4 =µ′4−4µ′3µ′1+6µ′2 (µ′1)2 − 3(µ′1)4

Относительный показатель эксцесса вычисляется в соответствии с:

α4 = µ4 µ22 .

Функции распределений случайной величины по нормальному и равномерному законам показаны на рис. 2.5.

В качестве стандарта принято значение отношения 4-го центрального момента к квадрату 2-го центрального момента для нормального распределения, оно равно 3. В связи с этим относительный показатель

2.1.4Оценка центральных моментов по результатам наблюдений

Если закон распределения случайной величины не известен, то оценки центральных моментов можно вычислить, заменяя µ'k на

56

N

mk' = (1/ N )∑ xik , (2.11)

i =1

где xi , - значения наблюдений; i [1,..., N ].

Рисунок 2.5 Функции распределений по нормальному и равномерному законам распределения

Оценка 2-го центрального момента вычисляется в соответствии с (2.6):

Уравнение (2.12) дает смещенную оценку дисперсии наблюдений. Несмещенная оценка вычисляется в соответствии с:

где x = m1' - эмпирическое среднее значение случайной величины. Эмпирическая оценка СКО получается как корень квадратный из оценки

дисперсии.

Оценка третьего центрального момента вычисляется по аналогии с (2.4):

Аналогично (2.10) относительный показатель эксцесса вычисляется по формуле:

57

2.1.5Квантили

Важной характеристикой при представлении информации о распределении является значение квантилей. Для непрерывной случайной величины с плотностью распределения p(x) q -квантилем является такое значение случайной величины z(q), при котором интегральная функция распределения равна q . То есть квантиль равен такому значению, при котором:

−∞

При определении квантиля для дискретной случайной величины в (2.18) интегрирование заменяется суммированием. Точного равенства в общем случае получить невозможно.

2.1.6Правила определения оценок и доверительных границ для параметров нормального распределения

При оценке результатов экспериментальных исследований необходимо оценить достоверность полученных данных. Рассмотрим правила определения доверительных границ при получении оценок моментов распределения случайных величин для случая нормального распределения. Она производится в соответствии с ГОСТ [13].

Определение доверительных границ для генеральной средней при неизвестной дисперсии. Определение нижней и верхней границы двустороннего доверительного интервала (mН , mВ ) для генеральной средней x осуществляется при заданной доверительной вероятности γ по случайной выборке объема N в соответствии с формулами:

t1+ γ (ν)

v=N-1 степенями свободы.

Значения величины 1 t1+ γ (ν) указаны в табл. 1 Приложения А для

N

2

q = (1 + γ)/ 2 .

58

Определение доверительных границ для генеральной дисперсии. Определение нижней и верхней границы двустороннего доверительного интервала (σ2 Н ,σ2 В )для генеральной дисперсии σ2 при заданной доверительной вероятности γ по случайной выборке объема N в

формуле

χq (ν) = 2ν2ν − 1 + uq ,

где uq - q -ый квантиль стандартизованного нормального распределения,

которую находят по табл. 2.1.

Доверительные границы для генерального среднего квадратического отклонения σ равны квадратным корням соответствующих доверительных границ для генеральной дисперсии, полученным по формулам (2.21), (2.22).

Выводы

Создание моделей цифровых изображений, разработка некоторых методов обработки изображений, обработка результатов экспериментальных исследований требуют знания теории вероятностей и математической статистики. В разделе дается основное представление о случайных величинах и распределениях. Приведены оценки моментов распределений. Большое внимание уделено нормальному закону распределения. Изложены правила определения оценок и доверительных границ параметров нормального распределения.

59

2.2Методы сегментации текстур

2.2.1Описание текстур

Текстура является важной характеристикой изображения. Проблема анализа текстур включает в себя такие аспекты, как описание текстур, их классификация, то есть формирование кластеров (при этом под кластером понимают обычно группу объектов, образующих в пространстве описания компактную в некотором смысле область), и сегментация, то есть разбиение изображения на области, однородные относительно одной или нескольких характеристик, или принадлежащие некоторому кластеру. Харалик [14] выделяет два подхода к описанию текстур: статистический и структурный. Сегодня можно сказать, что развит и получил распространение третий подход к описанию текстур - фрактальный. Более подробно эти подходы представлены в [1, 14, 15]. В [1] приведено определение текстуры, основанное на статистическом подходе к описанию текстур: «Под текстурами понимают такие типы изображений, класс которых обладает свойством эргодичности, то есть любое изображение данной текстуры является типовым и полностью характеризует все другие изображения, относящиеся к этому классу».

Такой подход позволяет выявлять статистические характеристики образца текстуры и считать их соответствующими любым другим образцам этой текстуры. В дополнение к методам оценки признаков текстур, рассмотренным в [1], более подробно остановимся на следующих методах формирования признаков текстур.

2.2.2Метод описания текстур моментами функции распределения яркости

Метод описания текстур моментами функции распределения яркости основан на оценке гистограммы изображения текстуры и определении моментов функции распределения яркости изображения. Такими моментами являются, прежде всего: математическое ожидание (МО) и дисперсия (СКО - среднее квадратическое отклонение, равно корню квадратному из дисперсии). Наряду с этим оцениваются минимальное и максимальное значение яркости изображения. В табл. 2.2 представлены оценки этих значений для некоторых текстур из альбома Бродатца [17]. На рис. 2.6 представлены эти текстуры.

Это один из самых простых методов описания текстуры, однако он не позволяет учитывать пространственные характеристики текстур.

Таблица 2.2 Яркостные характеристики текстур