
Luciv / МКОИ_пособие
.pdf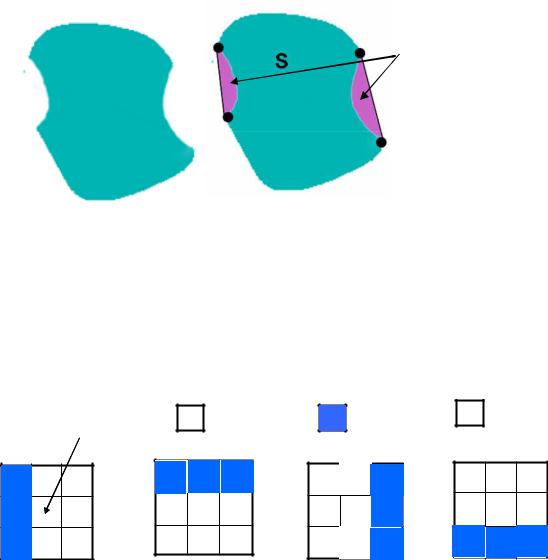
4.4Метод построения выпуклой оболочки границы
Для описания объектов используется построение выпуклой оболочки области интереса. Понятие выпуклой оболочки основано на определении выпуклого множества. Множество A называется выпуклым, если отрезок прямой, соединяющий любые две точки множества А, целиком лежит внутри А. Выпуклой оболочкой множества S называется наименьшее выпуклое множество H, содержащее S. На рис. 4.8 представлено множество S и его выпуклая оболочка H.
Множество D, полученное как разность множества H и множества S, называется дефектом выпуклости S:
D = H | S .
H
D
S
Рисунок 4.8 Определение выпуклой оболочки области.
Построение выпуклой оболочки выполняется по следующему морфологическому методу. Для каждого из 4-х структурирующих элементов (примитивов) Bi итеративно к множеству S применяется операция «успех/неудача» с последующим объединением с множеством S. Критерий останова: полученные множества на двух последовательных итерациях равны. Объединение полученных для каждого примитива множеств формирует выпуклую оболочку. Примитивы представлены на рис. 4.9.
|
|
|
|
=-1 |
|
|
центр |
|
|
X |
X |
|
|
|
|
X |
X |
|
X |
X |
X |
X |
X |
X |
|
= 1 |
X = 0 |
|
|
|
X |
X |
X |
X |
X |
X |
|
X |
|
X |
X |
X |
|
|
|
B1 |
B2 |
B3 |
B4 |
Рисунок 4.9 Структурирующие элементы морфологического алгоритма формирования выпуклой оболочки.
101

Операция «успех/неудача» выполняется в соответствии с (). На рис. 4.9 показано, как формируются примитивы B1 и B2 , используемые в ( ). Обращение к процедуре MATLAB bwhitmiss [] имеет вид:
BW2 = bwhitmiss (BW1, INTERVAL)/
Однако такой алгоритм приведет к построению выпуклой оболочки, но не минимальной.
В этом случае вместо двух массивов B1 и B2 передается один массив
INTERVAL. А примитивы B1 и B2 формируются логической операцией проверки равенства 1 и -1 соответственно. Например, для первого примитива массив INTERVAL имеет вид:
|
0 |
0 |
|
1 |
|
||
|
− 1 |
|
|
1 |
0 . |
||
1 |
0 |
0 |
|
|
|
|
|
Необходимо усложнить обработку, чтобы уменьшить увеличение области, например, ограничив разрастание области областью, построенной как описывающий область S прямоугольник R. С учетом этого можно представить алгоритм построения выпуклой оболочки в следующем виде.
Для каждого примитива i = [1,4] выполняются следующие действия:
Xi |
= S |
|
0 |
= [(Xi |
* Bi )U S]I R . |
Xi |
||
k |
k −1 |
|
Критерий останова по k равенство множеств на двух последовательных
итерациях: Xi |
= Xi |
, k = k |
F |
. |
k |
k −1 |
|
|
|
Di = Xi . |
|
|
|
|
k F |
|
|
|
|
4
Формирование выпуклой оболочки: H = UDi .
i =1
4.5Методы разбиения границы на сегменты
Для упрощения описания границы выполняют ее разбиение на отдельные сегменты. При этом описание границы сокращается. Мы рассмотрели методы разбиения границы 4.2.2 и 4.2.3, которые позволяют разбить границу и аппроксимировать ее отрезками прямой.
Данный метод разбиения границы связан с построением выпуклой оболочки области, как показано на рис. 4.8. Опорные точки, по которым производится разбиение границы на сегменты, определяются как точки границы, в которых происходит вход в область дефекта и выход из области дефекта. На рис. 4.8 эти точки отмечены черным цветом. Они позволяют разбить границу на участки выпуклости и вогнутости. Такой метод чувствителен к малым возмущениям границы и может породить много несущественных сегментов. Поэтому границу следует сгладить перед применением этого метода.
102
4.6Преобразование к главным осям
Преобразование к главным осям позволяет определить срединные оси области, то есть построить совокупности точек, равноудаленных от границы области на минимальное расстояние. Алгоритм состоит в итерационном удалении элементов границы при соблюдении выполнения следующих условий: элементы не являются концевыми, область остается связной после удаления элемента, не производится эрозии внутрь области.
Выполнение этих условий обеспечивается при одновременном выполнении условий (4.3) и последующем одновременном выполнении условий (4.4):
2 ≤ N ( p1 ) ≤ 6 |
||||||
|
T ( p1 ) = 1 |
|||||
|
||||||
|
|
|
|
|
|
(4.3) |
p2 p4 p6 |
= 0 |
|||||
|
p |
4 |
p |
6 |
p |
= 0 |
|
|
|
8 |
|
||
где N ( p1 ) - число ненулевых соседей элемента p1 ; T ( p1 ) - число переходов из 0 в 1 при обходе окрестности по часовой стрелке от элемента p2 до p2 .
Обозначения элементов окрестности элемента |
p1 представлены на рис. 4.10 |
|||||||||||||
а). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 ≤ N ( p1 ) ≤ 6 |
|
|
|
|
|
|
|
|
||||||
|
T ( p1 ) = 1 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
(4.4) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
p2 p4 p8 = 0 |
|
|
|
|
|
|
|
|
||||||
|
p |
2 |
p |
6 |
p = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p9 |
p2 |
p3 |
|
0 |
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p8 |
p1 |
p4 |
|
1 |
p1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) б) |
p7 |
p6 |
p5 |
|
1 |
0 |
|
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Рисунок 4.10 а) Обозначение элементов в окрестности элемента p1 ; б) |
|||||||||||
пример окрестности в бинарном изображении. |
|
|
||||||||||||
|
|
|
В примере, представленном на рис. 4.10 б) N ( p1 ) = 4 , T ( p1 ) = 3 . |
|||||||||||
|
|
|
Условия (4.3) |
выполняются |
для |
граничных элементов, которые |
||||||||
находятся на нижней или правой границе или в левом верхнем угле границы. Аналогично условие (4.4) выполняются для граничных элементов, которые находятся на верхней или левой границе или в правом нижнем угле границы (рис. 4.11). В этих случаях элемент p1 подлежит удалению.
Ограничение, накладываемое на значение N ( p1 ), предотвращает эрозию внутрь области (рис. 4.12 а) и не позволяет удалять концевые элементы (рис.
103
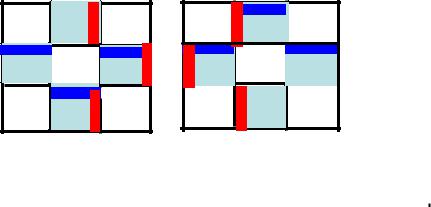
4.12 б). Ограничение, накладываемое на T ( p1 ), не позволяет нарушить связность (рис. 4.12 в).
p9 |
p2 |
p3 |
p9 |
p2 |
p3 |
p8 |
p1 |
p4 |
p8 |
p1 |
p4 |
|
|||||
p7 |
p6 |
p5 |
p7 |
p6 |
p5 |
а) б) |
|
|
|
|
|
Рисунок 4.11 а) Конфигурация элементов для условий (4.3); б) Конфигурация элементов для условий (4.4).
|
1 |
1 |
|
1 |
|
0 |
0 |
0 |
|
0 |
|
0 |
1 |
|
1 |
p1 |
|
0 |
|
1 |
p1 |
0 |
|
0 |
|
p1 |
0 |
|
|
|
|
|
|
0 |
0 |
0 |
|
1 |
|
0 |
0 |
а) б) в) |
1 |
1 |
|
1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 4.12 а) предотвращение эрозии внутрь области; б) элемент p1 является концевым; в) нарушение связности.
В соответствии с алгоритмом итерационно выполняется два прохода. При первом проходе рассматриваются все граничные элементы, проверяется выполнение (4.3), помечаются для удаления элементы p1 , для которых условие выполняется, после выполнения прохода помеченным элементам присваивается значение 0. При втором проходе проверяется выполнение условия (4.4) для оставшихся элементов границы, помечаются элементы для удаления, в которых выполняется условие (4.4), помеченным элементам присваивается значение 0. Критерий останова: нет элементов, помеченных для удаления.
Эта процедура позволяет построить остов области, в котором не нарушена связность.
4.7Методы описания области
После выполнения селекции связных областей по бинарному изображению, позволяющей промаркировать каждую область, формируются признаки этих областей. К ним относятся следующие признаки: геометрические признаки, характеристика формы; яркостные характеристики; цветовые характеристики; текстурные свойства. Геометрические признаки, цветовые характеристики были рассмотрены в [1].
104

4.7.1 Топологические дескрипторы областей
Для преобразований, при которых не происходит разрывов и склеек, топологические характеристики обладают инвариантностью к преобразованиям. Топологические характеристики определяются через число связных компонентов, число отверстий. На рис. 4.13 представлено изображение одной и той же области, подвергнутой деформациям.
Для этой области число связных компонентов равно 1, число отверстий равно 2. Область характеризуется числом Эйлера E в соответствии с уравнением:
E = C − H ,(4.4),
где С- число связных компонентов, Н- число отверстий.
а) б) в)
Рисунок 4.13 Топологические дескрипторы области а) исходное изображение; б) повернутое изображение а); в) растянутое по горизонтали и сжатое по вертикали изображение а).
Для области на рис. 4.13 число Эйлера равно -1.
Области, образованные отрезками прямых, также описывают числом Эйлера. В этом случае вводятся понятия вершин, ребер граней и отверстий, как показано на рис. 4.14.
грань
вершина
ребро
 отверстие
отверстие
Рисунок 4.14 Область, образованная отрезками прямой.
105
Если обозначить F- число граней, V- число вершин, Q – число ребер, то их соотношение с числом Эйлера устанавливается в соответствии с
формулой Эйлера: |
|
V − Q + F = C − H . |
(4.5) |
У области, показанной на рис. 4.14, число вершин равно 7, число ребер равно 12, число граней равно 2. Число Эйлера в соответствии с (4.5) равно: E=7–12+2=1-4=-3.
Кроме того, при описании области бывает полезным знать координаты описывающего прямоугольника, который является минимальным прямоугольником, содержащим эту область. Описывающий прямоугольник ориентирован вдоль координатных осей (x,y).
К геометрическим характеристикам относятся такие характеристики, как площадь, центр тяжести, координаты описывающего прямоугольника и периметр. Площадь равна количеству элементов изображения, принадлежащих области. Обозначим множество единичных отсчетов g(x,y) с координатами (x, y), принадлежащих области A, заданной в плоскости изображения как:
1, (x, y) A
g(x, y) = . (4.6)
0, иначе
Пусть координаты левого верхнего и правого нижнего углов прямоугольника, описывающего область, равны (X min ,Ymin ) и (X max ,Ymax ) соответственно. Тогда площадь вычисляется в соответствии с формулой:
Ymax |
X max |
|
S= ∑ |
∑g(x, y) . |
(4.7) |
y =Ymin x = Xmin |
|
|
Центр тяжести области задается координатами (X c ,Yc ) , определяемыми |
||
как среднее значение (x, y) координат, принадлежащих области в соответствии с уравнением:
X c = |
1 |
∑ x |
|
|
||
S |
|
|
||||
|
|
(x, y ) A |
. |
(4.8) |
||
|
1 |
|
|
|||
Yc = |
|
∑ y |
|
|
||
S |
|
|
||||
|
(x, y ) A |
|
|
|||
Определение координат центра тяжести объекта позволяет нормализовать положение объекта, определив положение начала координат в плоскости изображения, относительно которого положение объекта является центральным.
Если число граничных отсчетов области равно N, то длина периметра P равна сумме расстояний между соседними граничными точками:
N |
|
P = ∑ ri , |
(4.9) |
i=1
106

r = (x |
i+1 |
−x |
i |
)2 |
+ (y |
i+1 |
− y |
i |
)2 . |
(4.10) |
i |
|
|
|
|
|
|
Второй метод состоит в оценке периметра как числа граничных отсчетов области:
P = N . |
(4.11) |
Именно этот способ использован в пакете «Magisoft» [27]. Отсчет является граничным, если хотя бы один элемент из его окрестности не принадлежит области A.
В качестве характеристики формы используют оценку коэффициента
формы, определяемую как отношение квадрата периметра к площади: |
|
K = P2 S . |
(4.12) |
Для нормализации ориентации объекта при анализе бинарных изображений используется статистический подход [27, 28]. Объект описывают некоторым эллипсом рассеяния. В качестве ориентации выбирают направление собственного вектора x матрицы ковариации B координат отсчетов ненулевой яркости, то есть принадлежащих области A. Собственный вектор должен соответствовать максимальному собственному значению λ матрицы ковариации. Пусть матрица ковариации имеет вид:
B= B11 |
B12 , |
|
(4.13) |
B12 |
B22 |
|
|
где B ij - центральные моменты второго |
порядка: B11- |
дисперсия x- |
|
координаты ненулевых отсчетов яркости, |
B22 - дисперсия |
y-координаты |
|
ненулевых отсчетов яркости, B12 - ковариация (x,y)-координат |
ненулевых |
отсчетов яркости. |
|
Возможные собственные значения λ находятся из уравнения |
|
(B- λ E) x λ =0, |
(4.14) |
где E- единичная матрица, x λ -собственный вектор, соответствующий числу
λ .
Значения λ определяем из уравнения
B- λ E=0:
|
B11 |
|
B12 |
|
- λ |
1 |
|
0 |
|
=0 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
B12 |
|
B22 |
|
|
|
|
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B11 − λ |
|
|
B12 |
|
=0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
B12 |
|
B22 − λ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
(B − λ)(B − λ) − B |
2 |
|
= 0 ; |
|
|
|
|
|
|
|||||||||||||||||
11 |
|
|
22 |
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|||||
|
|
|
B |
|
|
+ B |
|
|
|
|
|
|
B |
|
|
+ B |
|
2 |
|
|
|
|
||||
λ |
= |
11 |
|
|
|
22 |
± |
|
|
|
|
|
11 |
22 |
|
− B |
B |
+ B 2 . |
(4.15) |
|||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
1,2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
11 |
22 |
12 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Собственные векторы находятся из уравнения (4.14): |
|
|||||||||||||||||||||||
|
B11 − λ1 |
|
|
B |
B12 |
|
|
|
|
× |
|
x1 |
|
= 0 ; |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
B |
|
|
|
|
|
− λ |
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|||||
|
12 |
|
22 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
107 |
|
|
|
|

(B11 − λ1)x1 +B12 x 2 = 0 ;
|
x1 = −B12 |
; |
||
x |
2 |
= B |
− λ |
|
|
11 |
1 |
|
|
tg ϕ = x 2 . x1
Размеры полуосей эллипса определяются Определяется соотношение собственных чисел (полуосей эллипса):
k = abs(λ2 ) ,
λ1
(4.16)
следующим образом. матрицы ковариации
где λ1 - большее собственное значение, λ2 - меньшее собственное значение. Площадь эллипса Square = πab . Отношение малой и большой полуосей
эллипса равно |
|
|
a / b = k . |
(4.17) |
|
Тогда Square = πkb2 . Большая полуось эллипса равна: |
||
|
|
|
b = Square /πk |
, |
|
где Square=S - площадь бинарного изображения (количество отсчетов с ненулевой яркостью).
Малая полуось эллипса определяется из уравнения (4.17): a= kb .
По бинарному изображению оцениваются параметры аппроксимирующего эллипса (в соответствии с рисунком 4.1): малая полуось a (в пакете «Magisoft» принято обозначение Dmin = 2a ), большая полуось b
(в пакете «Magisoft» |
принято обозначение Dmax = 2b ) и угол наклона |
большой оси эллипса |
ϕ (в пакете «Magisoft» принято название «Угол») в |
соответствии с описанным статистическим подходом к нормализации бинарного изображения объекта.
II |
|
|
I |
ϕ < 0 |
|
|
|
|
|||
|
|
|
b |
|
ϕ |
|
|
|
|
|
|
|
|
a |
x |
||
|
|
|
|||
III |
y |
|
|
IV |
ϕ > 0 |
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 4.15 Определение ориентации по собственному вектору матрицы ковариации.
108

4.8Выбор признаков. Анализ главных компонентов
Взадачах классификации важна роль выбора признаков объектов [29, 30]. Необходимо получить минимальный набор признаков, позволяющих идентифицировать исходные данные. Этого достигают при использовании метода главных компонентов, позволяющего выполнить декорреляцию признаков объектов.
Аннулирование корреляций между координатами. Для заданной n-
мерной случайной величины X найти такой ортонормированный базис, {a1,..., an }, в котором коэффициент ковариации между различными
координатами равен нулю. После преобразования к этому базису: cov(X i , X j )= 0 для i ≠ j ,
где cov(X i , X j )= E[(X i − X i )(X j − X j )] - коэффициент ковариации.
Диагонализация ковариационной матрицы. Все задачи о главных компонентах приводят к задаче диагонализации ковариационной матрицы или выборочной ковариационной матрицы. Эмпирическая или выборочная ковариационная матрица, это
C = [cij ],
|
1 |
m |
|
|
|
|
|
cij = |
∑ (xli − X i )(xlj − X j ). |
||||||
|
|||||||
|
|||||||
|
m − 1l =1 |
||||||
Векторы главных компонентов для задач о наилучшей аппроксимации и о поиске ортогональных проекций с наибольшим рассеянием - это ортонормированный набор {a1,..., an } собственных векторов эмпирической ковариационной матрицы C, расположенных в порядке убывания собственных значений λ : λ1 ≥ λ2 ≥ ... ≥ λn ≥ 0 . Эти векторы служат оценкой для собственных векторов ковариационной матрицы cov(X i , X j ). В
базисе из собственных векторов ковариационной матрицы она, естественно, диагональна, и в этом базисе коэффициент ковариации между различными координатами равен нулю.
Ортонормированный базис собственных векторов существует всегда, а собственные числа ковариационной матрицы всегда вещественны и неотрицательны.
Матрица преобразования к главным компонентам. Матрица A преобразования
данных к главным компонентам строится из векторов главных компонентов:
A = {a1,..., an }T . Здесь a j - ортонормированные векторы-столбцы главных
компонентов, расположенные в порядке убывания собственных значений, верхний индекс T означает транспонирование. Матрица A является ортогональной:
AT A = 1.
После преобразования большая часть вариации данных будет сосредоточена в первых координатах, что даёт возможность отбросить
109

оставшиеся и рассмотреть пространство уменьшенной размерности. Мы определим набор признаков со следующими свойствами:
Признаки независимы, поскольку собственные векторы ортогональны;
Проекция в базис {a1,..., ak } дает k-мерный набор линейных признаков, максимально передающих свойства исходного набора (имеющих максимальную дисперсию).
Нормировка после приведения к главным компонентам. После проецирования на
первые k главных компонентов с λ1 ≥ λ2 ≥ ... ≥ λn ≥ 0 удобно произвести нормировку на единичную (выборочную) дисперсию по осям. Дисперсия вдоль i-ого главного компонента равна λi > 0, (1 ≤ i ≤ k ), поэтому для нормировки надо разделить соответствующую координату на 
 λi . Это преобразование не является ортогональным и не сохраняет
λi . Это преобразование не является ортогональным и не сохраняет
скалярного произведения. Ковариационная матрица проекции данных после нормировки становится единичной, проекции на любые два ортогональных направления становятся независимыми величинами, а любой ортонормированный базис становится базисом главных компонентов. Отображение из пространства исходных данных на первые k главных компонентов вместе с нормировкой задается матрицей
|
a |
a |
|
|
|
|
a |
|
|
|
T |
|||||
|
2 |
|
|
k |
|
|
||||||||||
K = |
|
1 |
|
, |
|
|
|
,..., |
|
|
|
, |
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
λ |
|
λ |
2 |
|
|
|
λ |
|
|
|
||||
|
1 |
|
|
|
|
|
|
|
|
|
|
k |
||||
где |
a j |
|
- |
|
|
векторы-столбцы, верхний индекс T означает |
||||||||||
транспонирование.
Именно это преобразование чаще всего называется преобразованием Карунена-Лоэва.
5Основные понятия распознавания образов
Основные функции системы распознавания образов заключаются в обнаружении и выделении общих признаков образов, описывающих объекты, принадлежащие к одному и тому же классу образов, узнавании этого образа в любой другой обстановке и отнесении его к одному из заданных классов [31].
5.1Основные задачи систем распознавания образов
Первая задача состоит в представлении исходных данных, полученных как результаты измерений распознаваемого объекта. Когда измерения приводят к информации, представленной действительными числами, векторы образов можно рассматривать, как точки n-мерного евклидова пространства. Множество образов, принадлежащих одному классу, соответствует совокупности точек расположенных в некоторой области пространства измерений. Измеряемые параметры позволяют разделить множество образов на классы тогда, когда они формируют в евклидовом пространстве непересекающиеся множества.
110
