
Luciv / МКОИ_пособие
.pdfВторая задача распознавания образов связана с выделением характерных признаков или свойств из полученных данных и снижением размерности вектора образов. Признаки класса образов представляют собой характерные свойства, общие для всех образов данного класса. Признаки, характеризующие различия между отдельными классами, можно интерпретировать как межклассовые признаки. Задача состоит в выделении межклассовых признаков, позволяющих выполнить распознавание образов.
Третья задача состоит в отыскании оптимальных решающих процедур, необходимых при классификации. Пусть необходимо различить M классов, обозначенныхCi , i = [1, M ]. В этом случае пространство образов состоит из М областей, каждая из которых содержит точки, соответствующие образам из одного класса. Задача распознавания – построить границы областей решений, разделяющих M классов. Пусть эти границы определены решающими функциями di (x), i = [1, M ], где x -вектор образа. Эти функции, называемые дискриминантными функциями, являются скалярными и однозначными функциями образа x . Если di (x) > d j (x) для всех i, j = [1, M ] при j ≠ i , то
образ x принадлежит классу Ci . Структурная схема автоматической классификации представлена на рис. 5.1. БВРФ – блок вычисления решающих функций. Решающие функции определяются на основе априорной информации о распознаваемых образах. Если априорная информация неполная, создают систему последовательных корректировок решающих функций. В таких случаях используют обучающую процедуру. Первоначально выбирают произвольные решающие функции, а затем итеративно корректируют их, чтобы выполнить требования, предъявляемые к классификации.
Распознающая система должна адаптироваться к изменению распознаваемых объектов, обеспечивать помехоустойчивость работы. Цель распознающей системы состоит в отнесении каждого объекта к классу, признаки которого соответствуют признакам объекта.
5.2Концепции и методологии распознавания образов
При построении систем распознавания реализуют следующие принципы. Если класс характеризуется перечнем входящих в него членов, то система распознавания образов строится на принципе принадлежности этому перечню. Если класс характеризуется некоторыми общими свойствами, то построение системы распознавания основывается на принципе общности свойств. Если образы в пространстве описания образуют компактную в некотором смысле область, построение системы основывается на принципе кластеризации.
5.2.1Принцип общности свойств
Задание класса общностью свойств образов предполагает реализацию автоматического распознавания путем выделения подобных признаков. Общие свойства, или признаки, вводятся в память системы. При поступлении
111
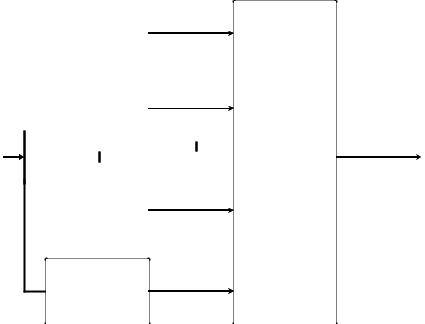
образа на вход системы, производится вычисление признаков и сравнение с признаками, заложенными в память. Образ относят к классу, описанному признаками, подобными признакам этого образа.
|
|
|
|
|
d1(x) |
|
|
|
|
|
|
БВРФ |
d2 (x) |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
БВРФ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
Блок |
x Ci |
|
|
|
|
||||
|
|
|
|
|
|
||
|
|
|
|
|
|
принятия |
di (x) = |
|
|
|
|
|
dM −1(x) |
решения |
|
|
|
|
|
|
|||
|
|
|
|
|
|
max [dk (x)] |
|
|
|
|
|
БВРФ |
|
|
|
|
|
|
|
|
|
k =[1,M ],k ≠i |
|
|
|
|
|
|
|
|
|
dM (x)
БВРФ
Рисунок 5.1 Структурная схема системы классификации образов
Эта концепция превосходит концепцию распознавания по принципу перечисления членов класса. Во-первых, для запоминания признаков необходимо меньше памяти, чем для запоминания всех образов, входящих в класс. Во-вторых, учитывая инвариантность признаков, обеспечивается правильная классификация при изменении характеристик образа. Если все признаки, определяющие класс, можно найти по имеющейся выборке образов, то процесс распознавания сводится просто к сопоставлению по признакам.
5.2.2Принцип кластеризации
Когда образы некоторого класса представляют собой векторы, компонентами которых являются действительные числа, этот класс можно рассматривать как кластер и выделять только его свойства в пространстве образов кластера. Системы распознавания определяют взаимное пространственное расположение кластеров. Если кластеры разнесены друг от друга, то применяется классификация по принципу минимального расстояния. Если кластеры пересекаются, то используются методы классификации с помощью функций правдоподобия, построения дискриминантных функций по заданной выборке образов с помощью итеративных обучающих алгоритмов. Методы основаны на детерминистском и статистическом подходах.
5.3Методы классификации
Существует три методологии построения систем распознавания: эвристическая, математическая и лингвистическая.
112
5.3.1Эвристические методы
Эти методы используют интуицию и опыт человека, основаны на принципах перечисления членов класса и общности свойств. Решение каждой задачи требует использования специфических приемов разработки системы. Структура и качество системы в значительной степени определяются опытом и знаниями разработчика.
5.3.2Математические методы
В основу положены правила классификации, которые формулируются и выводятся в рамках определенного математического формализма с помощью принципов общности свойств и кластеризации. Математические методы построения систем распознавания делятся на 2 класса: детерминистские и статистические.
Детерминистский подход основан на математическом аппарате, не использующем в явном виде статистические свойства классов образов.
Статистический подход основан на математических правилах классификации, которые формулируются в терминах математической статистики. Построение статистического классификатора предполагает использование байесовского классификационного правила и его разновидностей. Это правило обеспечивает получение оптимального классификатора, когда известны плотности распределения совокупности образов и вероятности появления образов для каждого класса.
5.3.3Лингвистические (синтаксические) методы
Если описание образов производится с помощью непроизводных элементов и их отношений, то для построения автоматических систем распознавания применяется синтаксический подход с использованием принципа общности свойств. Образ описывают как иерархическую структуру непроизводных элементов, аналогично структуре языка. Что позволяет использовать для распознавания теорию формальных языков. Грамматика образов содержит конечное множество элементов, называемых переменными, непроизводные элементы и правила подстановки.
Если существуют репрезентативные образы каждого рассматриваемого класса, используют методы «обучения с учителем». В этом случае система «обучается» распознавать образы с помощью адаптивных схем по обучающему множеству образов, классификация которых известна.
Если принадлежность элементов обучающего множества к определенным классам неизвестна, то такие методы называются распознаванием «без учителя».
В системах «обучения» адаптация производится на этапе обучения, далее система работает по критериям, отработанным на этом этапе. Качество распознавания определяется тем, насколько хорошо обучающие образы представляют реальные данные, с которыми система работает в процессе эксплуатации.
113
5.4Решающие функции
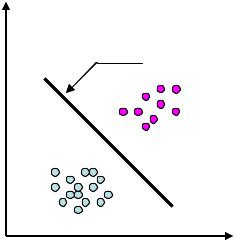
Основным назначением системы распознавания образов является отыскание решений о принадлежности предъявляемых образов некоторому классу. Один из подходов предполагает использование решающих функций. Пусть точками в двумерном пространстве признаков представлены образы 2 классов. На рис. 5.2 представлены две совокупности образов.
x2
d (x)
ω2 



 ω1
ω1
x1
Рисунок 5.2 Дискриминантная функция для случая 2 классов
Уравнение разделяющей прямой может быть представлено в виде:
d (x) = ω1x1 + ω2 x2 + ω3 = 0 , |
(5.1) |
||||
где ωi - параметры, xi -переменные. |
|
||||
|
Функцию d (x) можно использовать в качестве дискриминантной, |
||||
поскольку для каждого неизвестного образа x выполняются условия: |
|
||||
|
x ω1 |
, |
если |
d (x) > 0 |
|
|
x ω2 |
|
|
d (x) < 0 |
|
|
, |
если |
(5.2) |
||
не |
определено |
иначе |
|
|
|
Этот метод справедлив и для большего числа классов. Успех применения зависит от 2-х факторов: вида дискриминантной функции и практической возможности определения ее коэффициентов. Если рассматриваемые классы разделяются некоторыми решающими функциями, то для отыскания их коэффициентов можно использовать заданную выборку образов.
5.4.1 Линейные решающие функции
Функция (5.1) может быть обобщена на n-мерный случай.
d (x) = ω1x1 + ω2 x2 + ... + ωn xn + ωn +1 = w′x + ωn +1 |
(5.3) |
где = (ω1,ω2 ,...,ωn )- параметрический вектор. |
|
Если ввести в вектор образов x еще один компонент, равный 1, то есть представить:
x = (x1, x2 ,..., xn ,1) |
(5.4) |
|
114 |
= (ω ,ω |
2 |
,...,ω |
n |
,ω |
n +1 |
)′ , |
|
|
|
|
(5.5) |
|||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||
то решающая функция записывается в виде: |
|
|
|
|||||||||||||
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.6) |
d (x) = x . |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Вид решающих функций зависит от взаимного расположения классов. |
||||||||||||||
На рис. 5.3 показан пример, когда каждый класс отделяется от остальных с |
||||||||||||||||
помощью одной разделяющей границы (вариант 1): |
|
|
||||||||||||||
|
|
|
′ |
> 0, |
x |
ωi |
|
|
|
|
|
|||||
di (x) = i x |
|
|
x ωi |
|
|
|
|
(5.7) |
||||||||
|
|
|
|
|
< 0, |
|
|
|
|
|
||||||
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d2 (x) = 0 |
|
|
|
|
|
|||||
|
|
|
|
- |
|
+ |
|
|
d1(x) = 0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
+ |
- |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
ω1 |
|
|
|
ω2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
ОНР |
- |
(x) = 0 |
|
|
|
||
|
|
|
|
|
|
|
|
|
d3 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
x + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω3 |
|
|
|
|
|
Рисунок 5.3 Дискриминантные функции для 1 варианта |
|
|
||||||||||||||
ОНР – область неопределенности решения. |
|
|
|
|||||||||||||
|
|
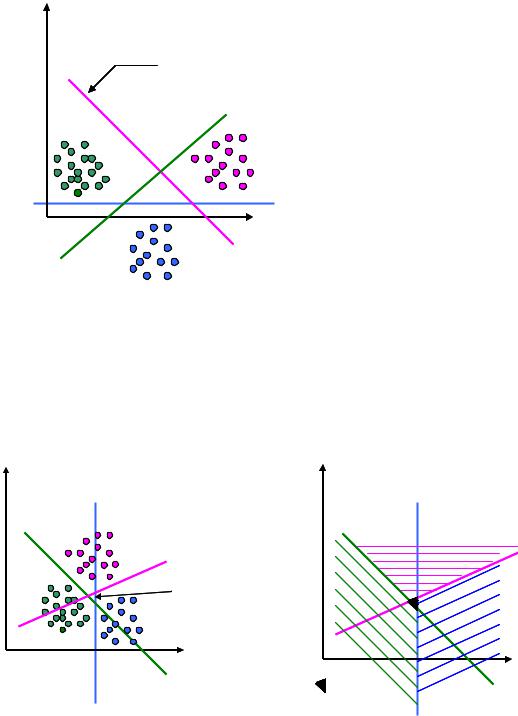
На рис. 5.4 показан пример, когда каждый класс отделяется от любого |
||||||||||||||
другого с помощью индивидуальной разделяющей поверхности (вариант 2- |
||||||||||||||||
классы разделимы попарно): |
|
|
|
|
||||||||||||
d |
ij |
(x) = w′ |
x |
|
|
|
|
|
|
|
|
|
|
(5.8) |
||
|
|
|
ij |
|
|
|
|
|
|
|
|
|
|
|
|
|
dij (x) > 0, |
x ωi , |
|
j ≠ i |
|
|
|
|
(5.9) |
||||||||
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
d12 (x) = 0 |
|
|
|
ω2 |
|
|
|
|
d12 (x) = 0 |
|
|
|||
|
|
+ - |
|
|
|
|
|
|
d23(x) = 0 |
+ - |
|
ω2 |
d23(x) = 0 |
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
+ |
- |
|
|
|
|
|
+ |
- |
|
|
ω1 |
|
|
|
|
|
|
|
ОНР |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
ω1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
ω3 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω3 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
- |
|
|
|
x1 |
|
|
|
|
x1 |
||
|
|
|
|
|
|
|
|
|
- ОНР |
+ |
- |
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
d13(x) = 0 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
Рисунок 5.4 Дискриминантные функции для 2 варианта |
d13(x) = 0 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
115 |
|
|
|
|
При этом выполняется условие: |
|
dij (x) = −d ji (x). |
(5.10) |
Если существуют такие дискриминантные функции, то классы ωi называются линейно разделимыми.
5.4.2Обобщенные решающие функции
Обобщение линейной решающей состоит во введении решающих функций вида:
|
|
|
K +1 |
|
|
|
d (x) = ω1 f1(x) + ω2 f2 (x) + ... + ωK f K (x) |
+ ωK +1 = |
∑ ωi fi (x), |
(5.11) |
|||
|
|
|
i =1 |
|
|
|
где {fi (x)}, |
i = [1, K ]- |
вещественные |
однозначные |
функции |
образа x , |
|
f K +1(x) = 1, |
K + 1 - число членов разложения. |
|
|
|
||
Если функции |
fi (x) - нелинейные, то |
и |
(5.11) – |
нелинейное |
||
преобразование. Уравнение (5.10) можно представить в виде линейной
функции нового образа x* , |
если выполнить преобразование образа x в этот |
|||||||||||
образ в соответствии с уравнением: |
|
|||||||||||
x* = [ f (x) |
f |
2 |
(x) . . |
. f |
K |
(x) 1]' . |
(5.12) |
|||||
1 |
|
|
|
|
|
|
|
|
|
|||
В этом случае уравнение (5.11) запишется в виде: |
|
|||||||||||
′ * |
, |
|
|
|
|
|
|
|
|
|
|
(5.13) |
d (x) = x |
|
|
|
|
|
|
|
|
|
|
||
где = (ω ,ω |
2 |
,...,ω |
K |
,ω |
K +1 |
)′ . |
|
|
||||
1 |
|
|
|
|
|
|
|
|
||||
При этом изменяется размерность нового вектора образа, если |
x - n- |
|||||||||||
мерный вектор, то x* - K-мерный, причем n может быть больше K. Решающие функции строят по репрезентативным выборкам образов
всех анализируемых классов.
5.5Классификация образов с помощью функций расстояния
Классификация образов с помощью функций расстояния - это система классификации, построенная на эвристическом подходе. Мерой сходства векторов образов, описываемых как точки в евклидовом пространстве, является их близость в этом пространстве. Критерий, принятый в соответствии с этой мерой – критерий минимума расстояния (от анализируемого образа до класса).
5.5.1Классификация образов по критерию минимума расстояния
Этот метод эффективен, когда изменчивость образов невелика, а влияние помех удается учесть.
Случай единственности эталона. Классификация эффективна, когда классы компактны.
Пусть есть M классов, каждый класс можно представить 1 эталонным образом zi , i = [1, M ]. Евклидово расстояние между вектором образа x и эталоном zi определяется в соответствии с:
116
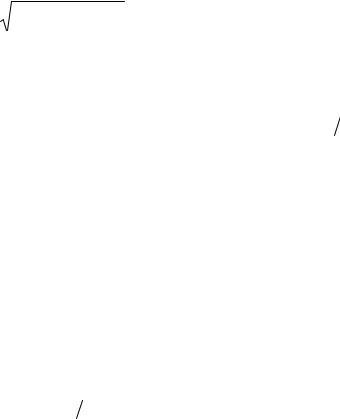
D = |
|
i |
|
= (x − z |
i |
)′ |
(x − z |
i |
) |
|
|
|
|
|
|
|
|
|
|
(5.14). |
||||||||||||||
x − z |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Образ x ωi , если j ≠ i Di |
< D j . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
Формулу (5.14) преобразуют к более удобному виду путем возведения в |
|||||||||||||||||||||||||||||||
квадрат обеих частей уравнения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
D2 |
= (x − z |
i |
)′ (x − z |
i |
) = x′x − 2x′z |
i |
+ z′ z |
i |
= x′x − 2[x′z |
i |
− (1 2)z′ z |
i |
]. |
|
(5.15) |
|||||||||||||||||||
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
i |
|
|
|
|
|
|
|
|||||||
|
|
|
Выбор min(D ) эквивалентен выбору min(D 2 ). Слагаемое x′x не зависит |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
i |
|
1 |
|
i |
i |
от номера класса, |
поэтому min(D 2 ) эквивалентен выбору max x′z |
|
− |
z |
′ z |
. |
||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
Дискриминантные функции определяются как |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
d |
|
(x) = x′z |
|
− |
1 |
z′ z |
|
, i = [1, M ]. |
|
|
|
|
|
|
|
|
|
|
(5.16) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
i |
|
|
|
i |
|
2 |
|
i |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Классификация выполняется в соответствии с: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
x ωi , если |
|
|
di (x) > d j (x) |
|
|
j ≠ i . |
|
|
|
|
|
(5.17) |
||||||||||||||||||||||
|
|
|
Дискриминантная функция di (x) является линейной. Покажем это. |
|||||||||||||||||||||||||||||||
Обозначим компоненты эталонных образов zij , |
j = [1, n].ωij = zij , |
|
j = [1, n]. |
|||||||||||||||||||||||||||||||
Обозначим ω |
i(n +1) |
= −1 2z′ z |
i |
. Дополним образ x единичным компонентом в |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
соответствии с (4.4). Тогда (5.15) можно представить в виде |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
= ∑ ωij x j . |
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.18) |
||||||||||||||
di (x) = i x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
j =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Линейная поверхность, разделяющая все пары эталонных точек zi , |
z j - |
||||||||||||||||||||||||||||||
это гиперплоскость, представляющая собой место точек, равноудаленных от эталонных точек.
Поскольку классификатор относит образы по критерию минимального расстояния, следовательно, анализируется наиболее полное совпадение образа с эталоном. Этот подход называют также корреляцией или сопоставление с кластером.
Множественность эталонов. Если класс определяет не один эталон, а
группа эталонов zli , то расстояние между анализируемым образом и классом
ωi |
оценивается по формуле: |
|
|
|
|||||||||
D = min |
x − zl |
|
, l = |
[1, N |
i |
], |
|
|
|
(5.19) |
|||
i |
l |
i |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где Ni - число эталонов для класса ωi . |
|
||||||||||||
|
|
Аналогично (5.16) решающие функции имеют вид: |
|
||||||||||
|
|
|
|
|
|
1 |
′ |
|
|
|
|
|
|
d |
(x) = max x′zl |
− |
|
(zl ) zl |
, l = [1, N |
i |
]. |
(5.20) |
|||||
|
|||||||||||||
i |
|
|
l |
i |
|
2 |
i |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Классификация производится в соответствии с (5.17).
117
Выявление кластеров. Умение находить в заданном наборе данных эталоны или центры кластеров играет главную роль в построении классификаторов по принципу минимума расстояния. В качестве меры расстояния мы использовали евклидово расстояние (5.14).
Существуют и другие меры сходства. Например, расстояние Махаланобиса. Расстояние Махаланобиса определяется для образов x и m в соответствии с уравнением при использовании статистического описания образов:
D = (x − m)′C −1(x − m), |
(5.21) |
где C -ковариационная матрица образов, m -вектор средних значений. Используются также неметрические функции сходства, например:
s(x, z) = |
|
x |
′ |
z |
|
= |
|
x′z |
. |
(5.22) |
|
|
|
|
|
|
|
|
|
||||
|
x |
|
z |
|
|
|
(x′x)(z′z) |
||||
|
|
|
|
|
|
|
|
||||
s(x, z) |
представляет |
собой косинус угла между векторами |
x и z |
||||||||
(рис.5.5).
Образ x будет отнесен к классу ωi , поскольку cos(θ1 ) > cos(θ2 ). Критерии кластеризации. Одним из показателей качества
кластеризации является сумма квадратов ошибки:
M |
2 , |
|
J = ∑ ∑ x − mi |
(5.23) |
i =1x Si
где M-число кластеров, Si - множество образов, принадлежащих i -му кластеру,
mi = |
1 |
∑ x |
(5.24) |
|
|||
|
Ni x Si |
|
|
где mi - вектор выборочных средних значений образов для множества Si , Ni -число образов, составляющих множество Si .
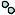

 z1
z1
x


 ωi
ωi
θ1
θ 2 |
z2 |
|
ω j |
Рисунок 5.5 Оценка сходства по косинусу угла θ между образом и эталоном
118
В качестве показателей качества могут быть выбраны такие показатели как: среднее значение квадратов расстояний между образами в кластере, среднее квадратов расстояний между образами, входящими в разные кластеры и др.
Примером выявления кластеров, например, является рассмотренный ранее алгоритм К внутригрупповых средних.
Оценка результатов кластеризации. При интерпретации результатов кластеризации полезно составить таблицу расстояний между центрами кластеров. Таблица 5.1 является примером таблицы расстояний.
Таблица 5.1 Таблица межкластерных расстояний
№ |
1 |
2 |
3 |
4 |
кластера |
|
|
|
|
1 |
0 |
5,1 |
20,1 |
30,8 |
2 |
|
0 |
25,1 |
12,3 |
3 |
|
|
0 |
10,6 |
4 |
|
|
|
0 |
Из табл. 5.1 следует, что расстояние между кластерами 1 и 2 существенно меньше расстояния между кластером 1 и другими кластерами. Дополнительно используют информацию о количестве образов, отнесенных к данному кластеру. В случае малого размера кластера решается вопрос о слиянии кластера или исключении его как принадлежащего шуму.
Кластеры сливаются в один, если расстояние между ними мало, и при этом число образов в одном кластере существенно меньше, чем в другом.
Важно учитывать дисперсию внутрикластерных отклонений, представляемую как n-мерный вектор, компонентами которого являются внутрикластерные дисперсии, вычисленные для каждого признака.
Существует много других методов оценки качества кластеризации. Распознавание кластеров можно рассматривать как задачу
распознавания образов без учителя. Пусть для заданного множества образов число классов неизвестно. С помощью алгоритмов кластеризации идентифицируют центры кластеров. Полученные кластеры считают классами образов. Эти классы могут быть использованы для получения дискриминантных функций с помощью алгоритмов обучения либо эти классы используют при классификации по функции минимума расстояния.
Таким образом, рассмотрена схема классификатора, действующего по принципу минимума расстояния в варианте с одним эталоном. Эта схема обобщена на случай многих эталонов. Подчеркнута важность проблем отыскания кластеров и задания эталонов. Когда принадлежность некоторому классу заданной выборки образов не известна, решается задача обучения без учителя. При этом в заданной выборке образов выделяются кластеры образов. Эти кластеры используются в качестве классов образов и используются для построения классификаторов.
119
5.6Классификация с помощью функций правдоподобия
Классификация с помощью функций правдоподобия основана на статистическом подходе. Этот подход применяется в тех случаях, когда случайные факторы влияют на порождение образов. Методы статистического анализа позволяют построить классификационное правило, позволяющее
получить наименьшую ошибку классификации в среднем. |
равна p(ωi |
|
x). |
|||
Пусть вероятность принадлежности образа x классу ωi |
|
|||||
|
||||||
При классификации образа x |
как образа, принадлежащего классу ω j |
|||||
обозначаются как Lij . Математическое ожидание потерь, |
связанных |
с |
||||
отнесением образа x к классу |
ω j , при числе классов M вычисляется |
в |
||||
соответствии с: |
|
|
|
|
|
|
M |
|
|
|
|
|
|
r j (x) = ∑ Lij p(ωi |
x). |
|
(5.25) |
|||
i =1
Эту величину называют средним риском, или условным средним риском. Образ x относят к классу, для которого средний риск минимален, а, следовательно, минимально математическое ожидание полных потерь. Классификатор, минимизирующий математическое ожидание общих потерь, называется байесовским.
В соответствии с формулой Байеса:
p(ω |
i |
|
x) = |
p(ωi )p(x |
|
ωi ) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.26) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
p(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
С учетом (5.26) выражение (5.25) можно записать в виде: |
|||||||||||||||||||||||||||||||
|
|
|
|
1 |
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
r j (x) = |
∑ Lij p(ωi )p(x |
ωi ) |
|
|
|
|
|
|
|
|
|
|
|
(5.27) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
p(x)i =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Функция p(x |
|
ωi ) называется функцией правдоподобия для класса ωi . |
|||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||
|
|
Общий для средних рисков множитель 1 p(x) можно не учитывать: |
|||||||||||||||||||||||||||||||
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r j (x) = ∑ Lij p(ωi )p(x |
|
ωi ) |
|
|
|
|
|
|
|
|
|
|
|
(5.28) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
i =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для случая M=2 средние риски равны: |
|
|
|||||||||||||||||||||||||||||
r (x) = L p(ω )p(x |
|
ω ) |
+ L p(ω |
2 |
)p(x |
|
ω |
2 |
), |
|
|
|
|
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
1 |
|
|
|
11 |
1 |
|
|
|
|
1 |
|
21 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
r2 (x) = L12 p(ω1 )p(x |
|
ω1 ) + L22 p(ω2 )p(x |
|
ω2 ). |
|
|
|||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
|
Образ x относится к классу ω , если r (x) < r |
(x), то есть: |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
2 |
|
(L21 − L22 )p(ω2 )p(x |
|
ω2 )< (L12 − L11 )p(ω1 )p(x |
|
ω1 ). |
|
(5.29) |
|||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||
Так как Lij > Lii , первые коэффициенты в обеих частях неравенства
положительны, следовательно, и обе части неравенства положительны. Из (4.28) следует
120
