FAQ_Print

('ABC','ABC') = 0

('ABC','ABCDEF') = 3 ('ABC','BCDE') = 3 ('BCDE','ABCDEF') = 2

Расстояние Левенштейна позволяет субъективно оценить, насколько строки не похожи друг на друга.

Для того чтобы получить дистанцию Левенштейна между строк s и t (длиной m и n соответственно, индексация начинается с нуля) и редакционное предписание (какие именно правки нужно вносить), рассчитывается матрица расстояний D (размерность m+1 * n+1), каждый элемент D[i, j] содержит дистанцию между первыми i символами строки s и первыми j символами строки t. Например, матрица дистанций Левенштейна для строк s='ABC' и t='ABF' (добавлены последние символы подстрок, чтобы соответствие было явно видно):

Столбцы соответствуют подстрокам строки t, а строки матрицы — подстрокам s. Строка и столбец с нулевым индексом соответствуют пустым подстрокам s и t. Каждый элемент этой матрицы содержит расстояние между подстроками соответствующих его индексам. Например, D[3,2] = 1 это расстояние между ABC и AB (всего одна правка — удалить C). Таким об-

разом, D[3,3] = 1 это и есть искомая дистанция между ABС и ABF. (замена C на F). Кроме дистанции эта матрица содержит в себе информацию о тех правках, которые необходимо внести в строку s чтобы получить строку t — редакционное предписание.

Построение матрицы дистанций похоже на прокладывание маршрута через лабиринт: начинаем из левого верхнего угла матрицы-карты и должны попасть в правый нижний. Часть матрицы можно заполнить без вычислений: столбец и строка с нулевыми индексами заполняются числами по порядку, начиная с нуля. Это просто объяснить тем, что для того, чтобы из пустой строки получить некую строку T (длиной k), нужно ровно k вставок — по одной на каждый символ. Аналогично и в обратную сторону: для того, чтобы из строки S длиной l получить пустую строку, нужно ровно l удалений. Таким образом, числа в нулевой строке и колонке не зависят от содержимого сравниваемых строк.

Остальные значения заполняются по следующим правилам:

Относительно ячейки D[i, j], ячейка, располагающаяся слева сверху от нее, D[i-1, j-1], представляет собой «пройденную дистанцию» — правки необходимые для того, чтобы первые i-1 символов строки s превратить в первые j-1 символов t.

Если s[i-1] = t[j-1], то значение можно скопировать из ячейки слева-сверху. Если же символы s[i-1] ≠ t[j-1], то возможны три варианта, из которых выби-

241

рается один с минимальной дистанцией:

Операция замены: символ s[i-1] нужно заменить на t[j-1]. В таком случае дистанция равна дистанции слева-сверху + 1.

Операция вставки: символ t[j-1] нужно вставить после на s[i-1] . Дистанция равна пройденной на образования t[0..j-2] из s[0..i-1] + одна операция вставки. Это движение вправо по карте. D[i, j] = D[i, j-1] + 1

Операция удаления: символ s[i-1] нужно удалить. Дистанция равна правкам, затраченным для образование t[0..j-1] из s[0..i-2] + 1 правка, отражающая удаление. Это можно сравнить с движением вниз по карте. D[i, j] = D[i -1, j] + 1

Пример:

A-A: символы совпадают, значение берем слева-сверху = 0

A-AB: символы различаются, слева 0, сверху-слева 1, сверху 2. берем минимальное значение + 1 = 1. Минимальное было слева, значит оптимальная операциявставка. Все

просто, чтобы A превратить в AB нужно вставить B.

A-ABF: A и F различаются, выбираем минимальное из 1, 2 и 3 и прибавляем 1. ( = 2) Минимальное зна-чение опять было слева, следовательно операция — снова вставка. Чтобы превратить A в ABF, нужно сначала получить AB (вставка) потом ABF(еще вставка)

Строка 2

AB-A: минимальное значение сверху (0), значит операция удаления (+1), итого правок 1. Чтобы из AB получить A нужно удалить B.

AB-AB: B и B совпадают, копируем дистанцию слева-сверху (0). Чтобы из ABполучить

AB никаких правок не нужно

AB-ABF: Вставка F + значение AB-AB = 0 + 1 = 1. Строка 3

ABC-A: минимальное значение сверху (1), добавляется опе-рация удаления (+1), итого 2 удаления: из ABС нужно уда-лить BC и получится A.

ABC-AB: снова минимальное значение

сверху(0), так как, чтобы ABC превратить в AB, нужно стереть C. Итого 1 правка.

242

ABС-ABF: слева-сверху 0 правок, слева 1, сверху тоже 1 правка. Выбирая наименьшее, мы выполняем замену C на F, что дает результирующее число правок равное 0+1 = 1

Искомая дистанция Левенштейна в этой матрице находится в правом нижнем углу, и вычисляется последней.

Редакционное предписание

Редакционное предписание — называется последовательность действий, необходимых для получения из первой строки второй кратчайшим образом. Обычно действия обозначаются так: D (англ. delete) — удалить, I (англ. insert) — вставить, R (replace) — заменить, M (match) — совпадение. Для строк ABC и ABF редакционное предписание будет выглядеть так:

M M R

A B C

A B F

10. Классификация образов на основе байесовской теории принятия решений.

Теорема. Формула Бейеса. (формула гипотез) Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, деленному на полную вероятность этого события.

В процессе регистрации объекта и измерения его характерных признаков получают множество чисел, которые составляют вектор наблюдения. Будем считать, что этот вектор наблюдений представляет собой случайный вектор с условной плотностью вероятности, зависящей от принадлежности этого вектора определенному классу. При распознавании объектов задачу формально сводят к

вероятностей этих гипотез заданы, т. е. известно, с какой вероятностью объект может принадлежать классу (или как часто появляется объект данного класса).

Пусть при реализации игры между природой и классификатором природа вы-

бирает класс - (стратегию игры) и предъявляет объект . Вероятность принад-

243

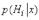лежности объекта классу обозначим как . Если классификатор прини-

мает решение о том, что объект принадлежит классу , когда на самом деле он

принадлежит классу , то классификатор несет потери, равные .Так как объект может принадлежать любому из рассматриваемых классов, то математическое ожидание потерь, связанных с отнесением наблюдаемого объекта к классу

, определяется следующим выражением:

в теории статистических решений эту величину часто называют условным средним риском или условными средними потерями.

При распознавании каждого объекта, предъявляемого природой, классификатор может отнести его к одному из возможных образов. Если для каждого объекта вычисляются значения условных средних потерь и классификатор причисляет объект к классу, которому соответствуют наименьшие условные потери, то очевидно, что и математическое ожидание полных потерь на множестве всех решений также будет минимизировано. Классификатор, минимизирующий математическое ожидание общих потерь, называется байесовским.

Пусть есть плотность распределения элементов вектора при условии, что он принадлежит классу . Вероятность принадлежности классу определяется формулой Байеса

безусловная плотность распределения (полная вероятность):

Принято считать (и это соответствует здравому смыслу), что потери от ошибочно принятого решения выше «потерь» при правильном выборе.

244

Байесовское решающее правило

Величину называют отношением правдоподобия,

величину пороговым значением критерия отношения правдоподобия.

11. Принципы работы и математический аппарат деревьев решений.

Что такое дерево решений и типы решаемых задач

Деревья решений – это способ представления правил в иерархической, последовательной структуре, где каждому объекту соответствует единственный узел, дающий решение.

Под правилом понимается логическая конструкция, представленная в виде "если ... то ...".

Область применения деревья решений в настоящее время широка, но все задачи, решаемые этим аппаратом могут быть объединены в следующие три класса:

•Описание данных: Деревья решений позволяют хранить информацию

оданных в компактной форме, вместо них мы можем хранить дерево решений, которое содержит точное описание объектов.

•Классификация: Деревья решений отлично справляются с задачами

классификации, т.е. отнесения объектов к одному из заранее известных классов. Целевая переменная должна иметь дискретные значения.

245

• Регрессия: Если целевая переменная имеет непрерывные значения, деревья решений позволяют установить зависимость целевой переменной от независимых(входных) переменных. Например, к этому классу относятся задачи численного прогнозирования(предсказания значений целевой переменной).

Первый узел нашего дерева "Возраст > 40?" является корнем дерева. При положительном ответе на вопрос осуществляется переход к левой части дерева, называемой левой ветвью, при отрицательном - к правой части дерева. Таким образом, внутренний узел дерева является узлом проверки определенного условия. Далее идет следующий вопрос и т.д., пока не будет достигнут конечный узел дерева, являющийся узлом решения.

Как мы видим, внутренние узлы дерева (возраст, наличие недвижимости, доход и образование) являются атрибутами описанной выше базы данных. Эти атрибуты называют прогнозирующими, или атрибутами расщепления (splitting attribute).

Каждая ветвь дерева, идущая от внутреннего узла, отмечена предикатом расщепления. Последний может относиться лишь к одному атрибуту расщепления данного узла. Характерная особенность предикатов расщепления: каждая запись использует уникальный путь от корня дерева только к одному узлу-решению. Объединенная информация об атрибутах расщепления и предикатах расщепления в узле называется критерием расщепления.

Преимущества деревьев решений

Интуитивность деревьев решений. Классификационная модель, представленная в виде дерева решений, является интуитивной и упрощает понимание

решаемой задачи. Результат работы алгоритмов конструирования деревьев решений легко интерпретируется пользователем.

Деревья решений дают возможность извлекать правила из базы данных на

естественном языке.

Алгоритм конструирования дерева решений не требует от пользователя выбора входных атрибутов (независимых переменных). На вход алгоритма можно подавать все существующие атрибуты, алгоритм сам выберет наиболее значимые среди них, и только они будут использованы для построения дерева.

Точность моделей, созданных при помощи деревьев решений, сопоставима с

другими методами построения классификационных моделей (статистические методы, нейронные сети).

Разработан ряд масштабируемых алгоритмов, которые могут быть использованы для построения деревьев решения на сверхбольших базах данных; масштабируемость здесь означает, что с ростом числа примеров или записей базы дан-

ных время, затрачиваемое на обучение, т.е. построение деревьев решений, растет линейно.

246

Быстрый процесс обучения. На построение классификационных моделей при помощи алгоритмов конструирования деревьев решений требуется значительно меньше времени, чем, например, на обучение нейронных сетей.

Большинство алгоритмов конструирования деревьев решений имеют возможность специальной обработки пропущенных значений.

Процесс конструирования дерева решений

Напомним, что рассматриваемая нами задача классификации относится к стратегии обучения с учителем, иногда называемого индуктивным обучением. В этих случаях все объекты тренировочного набора данных заранее отнесены к одному из предопределенных классов.

Алгоритмы конструирования деревьев решений состоят из этапов "построение" или " создание " дерева (tree building) и "сокращение " дерева (tree pruning). В ходе создания дерева решаются вопросы выбора критерия расщепления и остановки обучения (если это предусмотрено алгоритмом). В ходе этапа сокращения дерева решается вопрос отсечения некоторых его ветвей.

Критерий расщепления

Процесс создания дерева происходит сверху вниз, т.е. является нисходящим. В ходе процесса алгоритм должен найти такой критерий расщепления, иногда также называемый критерием разбиения, чтобы разбить множество на подмножества, которые бы ассоциировались с данным узлом проверки. Каждый узел проверки должен быть помечен определенным атрибутом. Существует правило выбора атрибута: он должен разбивать исходное множество данных таким образом, чтобы объекты подмножеств, получаемых в результате этого разбиения, являлись представителями одного класса или же были максимально приближены к такому разбиению. Последняя фраза означает, что количество объектов из других классов, так называемых "примесей", в каждом классе должно стремиться к минимуму.

Существуют различные критерии расщепления. Наиболее известные - мера энтропии и индекс Gini.

Энтропийный подход

Предположим что имеется множество А из n-элементов, m из которых облада-

ет свойством S. Тогда энтропией множества S называется соотношение H(A,S)= - m/n log(m/n) – (n-m)/n log((n-m)/n))

Энтропиясреднее количество битов, которое требуется чтобы закодировать атрибут S у элемента множества A (мера неопределенности)

Чем изменение энтропии больше, тем у атрибута больше шансов стать узлом. Предположим, что множество А элементов некоторые из которых обладают

247

свойством S классифи-цированы по средствам атрибута Q имеющее q возможных значений тогда приростA,S)-Ʃ(|Ai|/|A|)*H(информации определяется выражением

Gain(A,Q)=H( A,S)

Иначе говоря, на каждом шаге мы должны вычислить прирост информации и выбрать тот атрибут, при котором прирост максимальный.

Индекс Gini

Если дано множество T, включающее примеры из n классов, индекс gini(T), определяется по формуле:

где T - текущий узел, pj - вероятность класса j в узле T, n - количество классов.

Какой размер дерева может считаться оптимальным? Дерево должно быть достаточно сложным, чтобы учитывать информацию из исследуемого набора данных, но одновременно оно должно быть достаточно простым. Другими словами, дерево должно использовать информацию, улучшающую качество модели, и игнорировать ту информацию, которая ее не улучшает.

Тут существует две возможные стратегии. Первая состоит в наращивании дерева до определенного размера в соответствии с параметрами, заданными пользователем. Определение этих параметров может основываться на опыте и интуиции аналитика, а также на некоторых "диагностических сообщениях" системы, конструирующей дерево решений.

Вторая стратегия состоит в использовании набора процедур, определяющих "подходящий размер" дерева. Процедуры, которые используют для предотвращения создания чрезмерно больших деревьев, включают: сокращение дерева путем отсечения ветвей ; использование правил остановки обучения.

Остановка построения дерева

Рассмотрим правило остановки. Оно должно определить, является ли рассматриваемый узел внутренним узлом, при этом он будет разбиваться дальше, или же он является конечным узлом, т.е. узлом решением.

Один из вариантов правил остановки - "ранняя остановка" (prepruning), она

определяет целесообразность разбиения узла. Преимущество использования такого варианта - уменьшение времени на обучение модели. Однако здесь возникает риск снижения точности классификации. Поэтому рекомендуется "вместо остановки использовать отсечение" (Breiman, 1984).

Второй вариант остановки обучения - ограничение глубины дерева. В этом

случае построение заканчивается, если достигнута заданная глубина.

Еще один вариант остановки - задание минимального количества примеров,

248

которые будут содержаться в конечных узлах дерева. При этом варианте ветвления продолжаются до того момента, пока все конечные узлы дерева не будут чистыми или будут содержать не более чем заданное число объектов.

Сокращение дерева или отсечение ветвей

Качество классификационной модели, построенной при помощи дерева решений, характеризуется двумя основными признаками: точностью распознавания и ошибкой.

Точность распознавания рассчитывается как отношение объектов, правильно классифицированных в процессе обучения, к общему количеству объектов набора данных, которые принимали участие в обучении.

Ошибка рассчитывается как отношение объектов, неправильно классифицированных в процессе обучения, к общему количеству объектов набора данных, которые принимали участие в обучении.

Отсечение ветвей или замену некоторых ветвей поддеревом следует проводить там, где эта процедура не приводит к возрастанию ошибки. Процесс проходит снизу вверх, т.е. является восходящим. Это более популярная процедура, чем использование правил остановки. Деревья, получаемые после отсечения некоторых ветвей, называют усеченными.

12. Основы построения систем защиты от угроз нарушения конфиденциальности информации.

Схема традиционно выстраиваемой эшелонированной защиты:

Рис. 1. Структура системы защиты от угроз нарушения конфиденциальности информации

Как видно из приведённой схемы, первичная защита осуществляется за счёт

249

реализуемых организационных мер и механизмов контроля физического доступа к АС. В дальнейшем, на этапе контроля логического доступа, защита осуществляется с использованием различных сервисов сетевой безопасности. Во всех случаях параллельно должен быть развёрнут комплекс инженерно-технических

средств защиты информации, перекрывающих возможность утечки по техническим каналам.

Организационные меры и меры обеспечения физической безопасности

Данные механизмы в общем случае предусматривают:

•развёртывание системы контроля и разграничения физического доступа к элементам автоматизированной системы.

•создание службы охраны и физической безопасности.

•организацию механизмов контроля за перемещением сотрудников и посетителей (с использованием систем видеонаблюдения, проксимити-карт и т.д.);

•разработку и внедрение регламентов, должностных инструкций и тому подобных регулирующих документов;

•регламентацию порядка работы с носителями, содержащими конфиденциальную информацию.

Идентификация и аутентификация

Под идентификацией принято понимать присвоение субъектам доступа уникальных идентификаторов и сравнение таких идентификаторов с перечнем возможных. В свою очередь, аутентификация понимается как проверка принадлеж-

ности субъекту доступа предъявленного им идентификатора и подтверждение его подлинности.

Всё множество использующих в настоящее время методов аутентификации можно разделить на 4 большие группы:

1.Методы, основанные на знании некоторой секретной информации. Классическим примером таких методов является парольная защита.

2.Методы, основанные на использовании уникального предмета.

3.Методы, основанные на использовании биометрических характеристик че-

ловека.

4.Методы, основанные на информации, ассоциированной с пользователем. Примером такой информации могут служить координаты пользователя, определяемые при помощи GPS. Данный подход вряд ли может быть использован в качестве единственного механизма аутентификации, однако вполне допустим в качестве одного из нескольких совместно используемых механизмов.

250