Кочубей СПЕКТРОСКОПИЯ РАССЕИВАЮЩИХ СРЕД

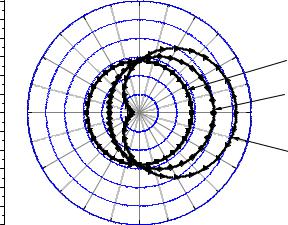
Рис. 15 представлена фазовая функция Эддингтона при различных значениях фактора анизотропии рассеяния. Хорошо видно, что фазовая функция Эддингтона значительно более изотропна по сравнению с фазовой функцией ХеньиГринштейна, что значительно ограничивает область ее применимости для моделирования распространения излучения в реальных биотканях.

Поскольку фазовые функции Хеньи-Гринштейна и Эддингтона являются наиболее часто используемыми при моделировании распространения света в биотканях, сравним их поведение при одних и тех же параметрах. На Рис. 16-18 представлены графики данных функций при различных значениях фактора анизотропии.

Рис. 15. Фазовая функция Эддингтона при различных значениях фактора анизотропии

распространения излучения в реальных биотканях, нужно очень внимательно подходить к выбору фазовой функции рассеяния.

Несмотря на столь явные различия в поведении этих функций несложно получить соотношения между параметрами данных функций позволяющие осуществлять переход от одной функции к другой. Раскладывая фазовую функцию

При разложении по полиномам Лежандра модифицированной функции Хеньи-Гринштейна

после приведения подобных членов, получим

39

Таким образом, уравнения (44) и (45) обеспечивают возможность пересчета параметров модифицированной фазовой функции Хеньи-Гринштейна в параметры фазовой функции дельта-Эддингтона. Так например, для фазовой

= 0.82

Переход от параметров фазовой функции дельта-Эддингтона к параметрам

процесс однократного рассеяния в биологических тканях более точно, чем функция Хеньи-Гринштейна. Функция Хеньи-Гринштейна является частным случаем функции Гегенбауэра при α=1/2.

Для функции Гегенбауэра фактор анизотропии g получается в соответствии с

равномерно распределенная в интервале (0; 1).

Для описания процесса однократного рассеяния на крупных частицах, примером которых могут служить эритроциты цельной крови человека, кроме

относительного коэффициента преломления n' рассеивателей.

Во многих случаях фазовую функцию рассеяния можно определить, используя результаты гониофотометрических измерений оптически тонкого образца ткани [42], а именно, измерить индикатрису однократного рассеяния

анизотропии подобной фазовой функции вычисляется следующим образом.

значения функции fn в точках, где экспериментальная информация отсутствует, используя процедуру сплайн-интерполяции, и вычислять значение фактора анизотропии численным интегрированием выражения (49).

Учет вклада рассеянного излучения в сигнал, регистрируемый детектором коллимированногопропускания

Используя закон Бугера, можно определить интенсивность света, прошедшего через рассеивающий и поглощающий образец без взаимодействий с рассеивателями или, другими словами, коллимированное пропускание образца. Однако, в действительности всякий детектор имеет ограниченное поле зрения, и поэтому нужно принимать во внимание вклад вперед рассеянного излучения в сигнал на детекторе коллимированного пропускания (рис. 19). В ситуациях, когда

многократно рассеянного света в измеряемый сигнал можно пренебречь и использовать для коррекций приближение однократного рассеяния теории переноса излучения. В случае оптически толстых образцов вклад многократно рассеянного света в "коллимированное" пропускание существенно возрастает и приближение однократного рассеяния уже не в состоянии адекватно скорректировать ситуацию. Если фактор анизотропии исследуемой среды достаточно высок, что характерно, например, для большинства биологических тканей, то для коррекций можно использовать малоугловое приближение теории переноса излучения.

42

внутри образца. Формула (54) не учитывает конечного размера падающего пучка и поэтому применима лишь для случая, когда rb>r1,r2 и d12>>rb, r1,r2 (см. рис. 20).

Рис. 19 Схематическое представление измерения коллимированного пропускания. rb - радиус падающего пучка, ds1 - расстояние между образцом и первой апертурой,d12 - расстояние между апертурами, r1 - радиус первой апертуры,r2 - радиус второй апертуры. Также на рисунке показан возможный "путь" квазибаллистического фотона.

В результате интегрирования (54) получается:

Полный поток однократно рассеянного света Fss, регистрируемый детектором дополнительно к ослабленному нерассеянному потоку F0, получается интегрированием лучевой интенсивности по принимающему углу детектора:

Эффективный приемный угол детектора рассчитывается с учетом разницы показателей преломления на пути между образцом и детектором. Наличие преломляющих поверхностей на пути света между образцом и детектором уменьшает угол приема детектора, если показатель преломления стекла ng выше показателя преломления окружающей среды na:

= ( ) (57)

Формула (57) не учитывает разницу показателей преломления образца и предметного стекла, что оправдано для большинства биотканей.

Интегрирование в формуле (56) осуществлялось численным методом Ньютона-Кортеса восьмого порядка.

43

рассеянного излучения в регистрируемый сигнал увеличивается. Если фактор анизотропии исследуемого образца довольно высок, а принимающий угол детектора коллимированного пропускания достаточно мал, то для учета вклада многократно рассеянного излучения можно использовать малоугловое приближение теории переноса излучения. Для экспериментальной конфигурации, показанной на рис. 20, можно использовать следующую формулу при вычислении лучевой интенсивности ISA рассеянного света в малоугловом приближении [44]:

== 1 −

Записывая уравнение (63), пренебрегают зависимостью коэффициента

рассчитывается численно.

Сигнал, регистрируемый детектором коллимированного пропускания, в

44

Многопотоковая теория Кубелки - Мунка

В условиях многократного рассеяния могут использьзоваться такие методы анализа распространения света, как, например, метод дисперсных ординат или многопотоковая теория Кубелки-Мунка [34, 65-67]. В многопотоковой теории можно выделить такие частные случаи, как двухпотоковая модель КубелкиМунка, трех-, четырех- и семипотоковая модели. Например, трехпотоковая модель включает два диффузных потока вперед и назад, а также коллимированный поток вперед, а семипотоковая модель состоит из 6-и диффузных потоков в трехмерном пространстве и коллимированного потока. Однако применимость модели Кубелки-Мунка и диффузного приближения ограничивается случаями, когда длина путей фотонов в среде не слишком мала и когда транспортный коэффициент рассеяния много больше коэффициента поглощения. Численные решения транспортного уравнения могут быть полезны только для сравнительно простых конфигураций объекта. Описание распространения света в более сложных моделях с помощью многопотоковой теории требует большого числа учитываемых потоков.

Для многослойных сред, в которых плоскопараллельные слои расположены по глубине образца, перпендикулярно направлению распространения света, используя простую трехпотоковую модель, значение толщины d, коэффициентов поглощения a и рассеяния s, параметра анизотропии g и показателя преломления n для каждого слоя, можно рассчитать распределение интенсивности в каждом слое. Примером таких объектов могут служить биологические образцы. Например, для 4-слойной модели кожи (эпидермис, верхняя дерма, кровеносные сосуды, нижняя дерма) расчеты показывают, что интенсивность света на =577 нм в эпидермисе примерно в два раза превышает интенсивность падающего пучка. В верхней дерме она падает от значения 1.75 до 0.3 от интенсивности падающего пучка, а в области кровеносных сосудов быстро падает до нуля.

В работе [68] рассмотрено использование трехпотоковой модели для исследования оптических свойств слизистой оболочки желудка. С этой целью были определены спектры коллимированного пропускания (Тс=F+(z)/Fco), полного пропускания (Td=F+(Z)/FCQ) И диффузного отражения от передней (Rd=Fo-/Fco) и задней границы (Rd2=F_(z)/Fco) ткани слизистой оболочки желудка. Здесь Fco - падающий световой поток; Fc(z) и F+(z) - соответственно прошедший коллимированный и диффузный потоки; Fo- и F_(z) — диффузные потоки, отраженные соответственно от передней и задней границы биологической ткани; z - толщина образца.

Экспериментальные данные (Td, Rd1,2, Тс) корректировались с учетом зеркального отражения на границе раздела воздух-стекло-биоткань по методике, описанной в [69]:

45

коэффициенты зеркального отражения на границе воздух-стекло и стеклобиоткань, соответственно равные ~ 0.0465 и ~ 0.004 [69]. Конечные данные диффузных измерений рассчитывались, используя следующие соотношения:

трехпотоковой модели Кубелки−Мунка [64] распределение света в среде представлено в виде дифференциально-разностных уравнений для трех потоков:

отражения, равный ~ 0.004 [6]; rid≈0.25, коэффициент внутреннего отражения от обеих границ биологической ткани, определенный как rid≈-1.44n-2+0.71n- 1+0.063n [70], п≈1.135, относительный показатель преломления на границе раздела образец-стекло [69].

В результате получено три выражения, связывающие потоки в среде у передней и задней границ объекта, в которых искомые величины (Td, Rd1,2, Тс) являются функциями этих потоков. Конечное решение может быть получено путем численного решения обратной задачи системы полученных уравнений (67) и (68), для чего в приведенной работе был использован метод Ньютона.

46

Диффузионное приближение теориипереноса излучения

Диффузионное приближение [71] оказывается хорошим приближением в случае малых значений фактора анизотропии однократного рассеяния (g≤0.1) и больших альбедо (∆→ 1). Например, для большинства биологических объектов g≈0.6-0.9, а для крови даже может достигать 0.995, это существенно ограничивает применимость диффузионного приближения. Считается, что при оптических толщинах объекта:

входе светового пучка, где преобладает однократное рассеяние. Основной идеей диффузионного приближения является разложение диффузной лучевой интенсивности в ряд Тейлора и ограничение ряда первыми двумя членами. Диффузионное приближение имеет ряд ограничений, наиболее существенными из которых являются следующие. Во-первых, для корректности диффузионного

говоря, может быть использовано лишь на больших оптических расстояниях от источников и границ. Это условие часто не выполняется для оптически тонких образцов биоткани. Однако корректный выбор соответствующих граничных условий в значительной мере снимает это ограничение, и дает достаточно хорошее согласование диффузионного приближения с экспериментальными данными и расчетами, выполненными с использованием более точных методов решения уравнения переноса излучения. В силу того, что диффузионное приближение позволяет получить достаточно строгое аналитическое решение уравнения переноса, что в свою очередь, обеспечивает требуемое быстродействие при проведении расчетов, оно широко используется в оптике биотканей и биомедицинской оптике.

Рассмотрим диффузионное приближение на примере плоского слоя сильно рассеивающего вещества, имеющего неограниченную ширину, длину и ограниченную толщину Слой равномерно освещается коллимированным светом, падающим по нормали к поверхности. Фазовая функция в данном случае выбрана в форме фазовой функции дельта-Еддингтона (35). Подстановка данной

47

Коллимированная составляющая включает как свет, рассеянный в направлении, параллельном падающему пучку, так и не рассеянный свет. Коллимированное излучение ослабляется со скоростью, пропорциональной

Углы падения и пропускания θ0 и θt связаны по закону Снелиуса:

=,

где ni и nt показатели преломления среды, из которой падает свет и среды, в

слое глубины z. Подставляя (71) в (70) и, упрощая с учетом (72) и (75), получим

48