
Кочубей СПЕКТРОСКОПИЯ РАССЕИВАЮЩИХ СРЕД
.pdf
излучения. Определим функцию перераспределения h u, как долю света,
рассеянного из конуса с углом u в конус с углом . Заметим, что функция перераспределения является оператором пропускания для единичного акта рассеяния. Функция перераспределения рассчитывается с помощью усреднения фазовой функции по всем возможным азимутальным углам при фиксированных углах u и .
|
|
|
|
h u, |
1 |
2 |
p u |
|
|
|
|
|
d |
|
|
|
|
|
|
|
1 u2 |
|
1 2 |
cos |
|
||||
|
|
|
|
2 |
(192) |
|||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||
v 1), |
Если косинус угла падения или выхода излучения равен единице (u 1 или |
|||||||||||||
то |
|
функция перераспределения |
|
эквивалентна |
фазовой |
функции |
||||||||
|
|
|
. В случае изотропного рассеяния функция |
перераспределения |
||||||||||
h 1, |
|
p |
|
|||||||||||
обращается в константу и равна h u, 1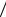 4 .
4 .
Для случая, когда для расчетов используется фазовая функция в форме Хеньи-Гринштейна, функция перераспределения может быть выражена в терминах полного эллиптического интеграла второго рода:
h u, |
|
1 g2 |
|
2 |
E k |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
. |
|
|
|
|||
где g - средний косинус угла рассеяния, E k |
|
|
|
|
|
|
|
|
||||||
|
- полный эллиптический интеграл |
|||||||||||||
второго рода и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 g2 2gu , 2g |
|
|
|
|
|
|
|
k |
2 |
|
|
|||
1 u2 |
|
1 2 , |
||||||||||||
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Применение других фазовых функций требует численного интегрирования уравнения (192). Если фазовая функция сильно анизотропна, то интегрирование по азимутальному углу несколько затруднено, и необходимо внимательно следить за точностью интегрирования. Это важно, поскольку ошибка при вычислении функции перераспределения прямо влияет на точность вычисления операторов отражения и пропускания для тонких слоев. Эти ошибки удваиваются при каждом успешном сложении слоев, и малая ошибка в процессе вычислений будет быстро возрастать.
Нормировка фазовой функции обеспечивает проверку точности квадратурного метода:
1 |
n |
h i, j h i |
, j |
|
|
wi |
1 |
|
|||
|
|
||||
2 i 1 |
|
|
, |
(193) |
|
|
|
||||
где n - число используемых квадратурных углов и знак "минус" во втором члене показывает "отраженную" компоненту рассеянного света. Если выражение (193) не удовлетворяется, то число квадратурных углов должно быть увеличено.
69
Отражение и пропускание тонкого слоя
Инициализация метода ДУ требует знания операторов отражения и пропускания для тонкого слоя. Функцию отражения R , можно определить
как количество излучения, отраженного слоем в направлении для света конически падающего от направления . Отражение нормируется на падающий диффузный поток излучения. Говоря другими словами, функция R , это
отношение подлинной функции отражения к функции отражения от идеально белой Ламбертовой поверхности. Функция пропускания определяется аналогичным образом.
Функция отражения (в случае однократного рассеяния) для тонких слоев описывается уравнением (194), за исключением случая, когда угол падения равен
углу преломления 0 0. В этом случае |
R a, ,0,0 . |
|
|
|
||||||||||||||||||
R a, , , 0 |
|
a h |
, 0 |
1 e |
|
0 |
|
|
||||||||||||||
|
0 |
|
|
|
|
|
|
(194) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Когда угол падения не равен углу |
преломления 0 , то |
функция |
||||||||||||||||||||
пропускания определяется как: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
T a, , , 0 |
a h , 0 |
|
e |
|
0 e |
|
|
|
|
|
||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
||||
Когда 0 , то основной луч (с конусом падения ) должен учитываться |
||||||||||||||||||||||
при расчете функции пропускания: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
T a, , , 0 |
|
a h , |
e |
|
|
1 |
e |
|
|
|
|
|||||||||||
|
|
|
|
|
|
2 |
|
. |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Заметим, что при 0 |
0 |
пропускание |
|
становиться |
нулевым: |
|||||||||||||||||
T a, ,0,0 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Отражение и пропускание слоя, образованного композицией двух тонких слоев
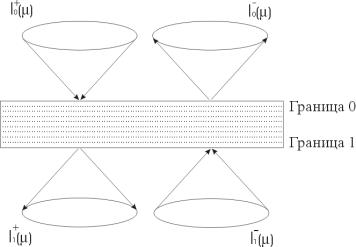
Определим Tnm и Rnm как операторы пропускания и отражения для света, падающего на сторону n и выходящего со стороны m одиночного слоя рассеивающей среды. Однородные слои биотканей не имеют избранных направлений, и, следовательно, матрицы Tnm и Rnm будут симметричными, т.е. Tnm Tmn и Rnm Rmn . Пусть вектор I0 определяет интенсивность излучения,
падающего со стороны 0 на слой 01, и пусть I1 интенсивность излучения,
падающего на слой со стороны 1 (Рис. 21). Аналогично определим I0 и I1 как интенсивности излучения, выходящего из слоя рассеивающей среды
70
соответственно через стороны 0 и 1. Излучение, идущее вниз от стороны 1, складывается из суммы прошедшего излучения, падающего со стороны 0, и излучения отраженного от стороны 1:
I T |
I R |
I |
(195) |
||
1 |
01 |
0 |
10 |
1 . |
|
Излучение, идущее вверх от стороны 0, складывается из излучения, |
|||||
прошедшего со стороны 1 и излучения, отраженного от стороны 0: |
|
||||
I T |
I R |
I |
(196) |
||
0 |
10 |
1 |
01 |
0 . |
|
Аналогичные формулы получаются для слоя 12. |
|
||||
I T |
I R |
I |
(197) |
||
2 |
12 |
1 |
21 |
2 |
|
I T |
I R |
I |
(198) |
||
1 |
21 |
2 |
12 |
1 |
|
Объединяя слои 01 и 12, получим комбинированный слой 02. Уравнения, описывающие интенсивность излучения, выходящего через верхнюю и нижнюю поверхности комбинированного слоя, будут иметь вид:
I T |
I R |
I |
(199) |
||
2 |
02 |
0 |
20 |
2 , |
|
I T |
I R |
I |
|
||
0 |
20 |
2 |
02 |
0 . |
|
При этом предполагается, что операторы отражения и пропускания для слоев 01 и 12 известны. Операторы отражения и пропускания для слоя 02 будут выражаться в терминах тех же операторов для слоев 01 и 12. Для этого умножим
уравнение (195) на R12 и сложим его с уравнением (198). Поскольку члены, |
|
содержащие I сокращаются, то получаем: |
|
1 |
|
E R12R10 I1 R12T01I0 T21I2 |
(200) |
. |
|
Умножая уравнение (200) на E R12R10 1 получим:
I1 E R12R10 1 R12T01I0 T21I2 .
Это уравнение определяет идущее вверх, через границу раздела двух слоев, излучение. Уравнение для излучения идущего вниз может быть получено аналогичным образом, с помощью уравнений (195) и (198):
|
|
|
I1 E R10R12 1 T01I0 R10T21I2 |
. |
|
(201) |
||||
|
|
|
|
|
|
|
|
|
||
Подставляя уравнение (201) в уравнение (197) получим: |
|
|
||||||||
|
|
|
E R10R12 |
1 |
|
|
1 |
|
|
|
I2 |
T12 |
|
T01 I0 |
T12 E R10R12 |
R10T21 |
R21 I2 |
||||
|
|
|
|
|
|
|
|
|
|
. (202) |
Сравнение уравнения (202) с уравнением (199) показывает, что:
|
T02 |
T12 E R10R12 1T01 |
, |
|
(203) |
|
|
|
|
|
|
||
R20 |
T12 E R10R12 1 R10T21 |
R21 |
. |
(204) |
||
|
|
|
|
|
||
Аналогично, подставляя уравнение (196) в уравнение (198) получим:
71
|
T20 |
T10 E R12R10 1T21 |
, |
|
(205) |
||
|
|
|
|
|
|
||
R02 |
T10 |
E R12R10 1 R12T01 |
R01 |
. |
(206) |
||
|
|
|
|
|
|
||
Уравнения (203-2 06) определяют операторы отражен ия и пропускания для слоя, состоящего из двух индивидуальных слоев, в терминах операторов отражения и пропускания каждого слоя.
Таким образом, п рименяя представленную последовательность действий требуемое число раз, мы можем найти отражение и пропускание слоя произвольной толщины.
Рис. 21 Распространение света через слой рассеивающей среды
Граничные условия
Пусть r - френелевское отражение на границе раздела двух слоев. Тогда
для света, проходящего из среды с показателем преломления n0 в среду с показателем преломлен ия n1, имеем:
|
R01 i |
, j |
|
r i |
|
ij |
|
|
|
|
|||||||||
|
2 i |
, |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
T |
|
|
|
|
1 r i |
n 2 |
|
|
|
||||||||||
, |
j |
|
|
|
|
|
|
|
1 |
|
|
ij |
|||||||
2 |
|
|
|
|
|||||||||||||||
01 |
i |
|
|
|
n |
|
|
||||||||||||
|
|
|
|
|
|
|
|
i |
|
|
0 |
. |
|||||||
Операторы отражения и пропускания, для света проходящего из среды 1 в |
|||||||||||||||||||
среду 0, будут определяться формулами: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
R10 i, j R01 |
i, j |
, |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T , |
j |
T |
|
|
|
n |
|
4 |
|
|
|||||||||
, |
|
|
|
0 |
|
|
ij |
||||||||||||
|
|
||||||||||||||||||
10 |
i |
|
|
01 |
i |
j n |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
. |
|||||||
72
Поскольку свет преломляется на границе, то необходимо контролировать, что бы падающие и преломленные потоки излучения соответствовали одним и тем же углам.
Если обеим сторонам слоя соответствуют одинаковые граничные условия, то, из-за симметрии, операторы отражения и пропускания, для света, проходящего сверху вниз и для света, проходящего снизу вверх, будут эквивалентны. Это дает возможность проведения быстрых вычислений для случая, когда граничные условия на верхней и нижней границах образца эквивалентны.
Рассмотрим трехслойную рассеивающую среду. Обозначим верхний слой среды как 01, средний слой 12 и нижний слой 23. Граничные условия на каждой стороне будут равны: R01 R32, R10 R23, T01 T32, T10 T23 . Например, свет, отраженный от слоя 01 (проходящий через границу 0 к границе 1), будет равен количеству света, отраженного от слоя 32, в силу отсутствия физических различий между этими двумя случаями. Данное переключение в нумерации следует из того, что свет, проходящий через среду наружу, через верхнюю поверхность, движется от 1 к 0, и от 2 к 3, при его прохождении через нижнюю границу. Отражение и пропускание композитного слоя, с учетом граничных условий, будут соответственно R30 и T03 .
T02 T12 E R10R12 1T01
R20 T12 E R10R12 1 R10T21 R21
T03 T10 E R20R10 1T02
R30 T10 E R20R10 1 R20T01 R01
Последовательность основных шагов метода ДУ Суммируя вышесказанное, сформулируем основные шаги представленного
метода.
Выбрать квадратурную схему интегрирования, т.е. определить число квадратурных точек. Необходимо отметить, выбор вами числа квадратурных точек определяет точность интегрирования и соответственно вычисления фазовой функции при каждом акте рассеяния. Квадратурный метод интегрирования в данном случае является аналогом разложения рассеянного излучения в ряд по сферическим гармоникам (так называемое PN приближение), рассмотренного в предыдущей главе. При этом, если число квадратурных точек N, то это соответствует PN 1 разложению, т.е. четыре квадратурные точки по точности соответствуют P3 аппроксимации.
Инициализировать оптически тонкий начальный слой.
73
Удваивая толщину начального слоя до получения требуемой толщины, рассчитать операторы отражения и пропускания слоя.
Выполнить данную процедуру для каждого слоя при моделировании многослойной среды.
Объединить слои с учетом граничных условий рассчитать отражение и пропускание многослойной среды.
Проверка метода показывает, что собственная погрешность метода не превышает 3% при использовании четырех квадратурных точек (метод механических квадратур) [72].
Инверсный метод добавления – удваивания представляет собой общее численное решение уравнения переноса излучения. Этот метод [73] был выбран, потому что он позволяет достаточно быстро получить решение на современных компьютерах, и достаточно гибок, для того чтобы можно было учитывать анизотропию рассеяния и внутреннее отражение, возникающее на границах образца. Другие решения уравнения переноса излучения, такие как: метод X и Y- функций Чандрасекара [74], метод дискретных ординат [75], метод статистического моделирования Монте-Карло [76-78], и многие другие – либо слишком медленны, либо недостаточно гибки, для того чтобы включать в себя граничные условия, необходимые для расчета распространения излучения в сильно рассеивающих средах, имеющих показатель преломления отличный от показателя преломления окружающей среды.
При использовании данного метода делают следующие предположения относительно уравнения переноса, формы образца и эксперимента:
1)уравнение переноса записывается в форме, не зависящей от времени;
2)образец состоит из однородных плоскопараллельных бесконечных слоев конечной толщины;
3)слои образца имеют однородные рассеивающие и поглощающие
свойства;
4)слои однородно освещаются коллимированым или диффузным светом. В основном эти предположения ограничивают тип и форму образцов, но
не противоречат известному характеру распространения света в них. Метод, ограниченный только этими предположениями будет пригоден для решения большого числа проблем оптики.
Недостатками метода добавления-удваивания являются:
невозможность расчета распределения излучения внутри исследуемой среды;
ограничения, накладываемые на форму образца, заключающиеся в том, что образец должен представлять собой равномерно освещенный бесконечный слой конечной толщины;
необходимость того, чтобы каждый слой был однороден по своим оптическим свойствам.
74
Несмотря на ограничения, которые метод добавления-удваивания накладывает на геометрию образца (образец должен состоять из однородных слоев и быть равномерно освещен), он весьма пригоден для итеративных вычислений, поскольку он обеспечивает точное вычисление коэффициентов диффузного отражения и полного пропускания образца, при сравнительно малых затратах машинного времени. Кроме того, его главным преимуществом перед диффузионным приближением теории переноса излучения (которое так же обеспечивает быстрое проведение расчетов коэффициентов диффузного отражения и полного пропускания в слоевой геометрии), является то, что соотношение коэффициентов поглощения и рассеяния исследуемой среды может быть практически любым, что позволяет проведение расчетов не только для сильно, но и для слабо рассеивающих сред.
Кроме вышеперечисленных ограничений необходимо, чтобы образец имел однородный показатель преломления, внутреннее отражение на границах раздела слоев подчинялось законам Френеля, образец не должен иметь внутренних источников излучения, и падающее на образец излучение должно быть неполяризованным.
Поскольку метод добавления-удваивания подразумевает азимутальную симметрию, то направление распространения световых лучей определяется углами, которые они образуют с нормалью к поверхности образца.
Метод Монте-Карло
Альтернативой аналитическому решению уравнения переноса является моделирование процесса распространения света в мутной среде методом МонтеКарло [79,80]. Алгоритм предназначен для определения величин диффузного отражения и полного пропускания, функций (r) и U(r), представляющих собой распределение освещенности внутри среды, а так же функций распределения прошедшего и отраженного излучения для плоской, многослойной, рассеивающей и поглощающей свет среды, на одну из поверхностей которой падает монохроматическое излучение. Каждый слой среды характеризуется следующим набором параметров ai , si , pi (sr,sr '),di ,ni , где di, ni - толщина и показатель преломления i-го слоя среды. Пространственно-угловое распределение падающего излучения можно представить в факторизованном виде:
S rr,sr A sr E rr , |
(207) |
где A sr описывает угловое распределение источника единичной мощности. Предполагается также, что падающий пучок имеет радиальную симметрию.
Блок-схема статистического метода моделирования Монте-Карло приведена на Рис. 22. Основные определения и этапы моделирования можно описать следующим образом.
75

Рис. 22 Блок-схема метода статистического моделирован ия Монте-Карло
Поскольку задача симметрична относительно сдвига в плоскости, параллельной поверхностям раздела между слоями, при м оделировании можно не учитывать пространственное распределение падающего излучения рассматривать точечный источник, помещенный в начало координат, с угловым распределением излучения A sr . Затем определяются функции Грина отклика среды на "точечное" внешнее воздействие G(rr), GT (rr), GR (rr) , которые определяют распределение полно й освещенности в среде, а так же поверхностное распределение прошедшего и отраженного света. Функции и U(r) вычисляются путем инте грирования:
76
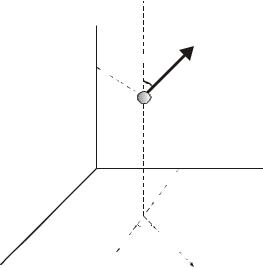
U(x, y,z) G(x , y ,z)E(x x , y y )dx dy , |
(208) |
i (x, y) Gi (x , y )E(x x , y y )dx dy , |
(209) |
где i R, T ; x,y,z - декартовы координаты радиус-вектора r .
Непосредственно статистическое моделирование включает в себя следующие шаги. Интересующая нас область разбивается на пространственные ячейки (i, j, k). Пределы этой области выбираются следующим образом. Пусть N -
N
число слоев среды, тогда d di - суммарная толщина всех слоев среды и
i 1
0 z d . Область в плоскости (x, y) выбирается так, чтобы часть излучения, попадающая за ее пределы, была пренебрежимо мала.
При инициализации фотон помещается в начало координат и ему присваивается исходный вес, равный W0. Каждый фотон характеризуется тремя координатами (x, y, z) и двумя углами ( , ), определяющими направление его движения (Рис. 23). Угол отсчитывается от положительного направления оси Z, а угол - от положительного направления оси X в плоскости (x, y). Если среда освещается коллимированным источником света, то начальное направление движения фотона считается совпадающим с направлением оси Z, которая направлена внутрь среды. Если же среда освещается диффузным источником света, то начальное направление распространения фотона выбирается случайным образом из всех направлений для которых косинус угла положителен.
Z
S

Фотон
Y
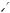


X
Рис. 23 Координаты фотона и углы, описывающие направление его движения
Затем вычисляются направление движения фотона и длина его пробега на данном шаге моделирования. Для этого используется формула:
77

|
p x dx |
|
xmin |
, |
(210) |
|
где - случайное число, равномерно распределенное в интервале (0,1), p(x) - функция плотности вероятности случайной величины x. xmin - минимальное значение x, xrnd - выбираемое значение x.
Для расчета длины свободного пробега фотона s используется функция плотности вероятности p( s) t exp( t s). Подставляя ее в формулу (210) и интегрируя, получаем формулу для расчета длины свободного пробега фотона:
s ln(1 )/ t .
Для определения направления движения фотона используются направляющие косинусы x, y , z между направлением движения фотона и
осями координат. Для фотона, локализованного в точке с координатами |
x, y,z , |
|
при перемещении его на расстояние s, в направлении |
x, y , z , |
новые |
координаты могут быть вычислены по формулам (211). |
|
|
x x x s |
|
|
y y y s |
|
|
z z z s |
|
(211) |
В случае рассеяния фотона на угол , от направления, в котором до этого происходило его распространение, новое направление распространения будет
определяться |
направляющими косинусами |
|
|
|
||||||||||
x |
, y , |
z , определяемыми |
||||||||||||
соотношением (212). |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
x |
sin |
|
|
x z cos y sin x cos |
||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
1 z2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
sin |
|
|
y z cos x sin y |
cos |
||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
1 z2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
z sin cos 1 z2 z |
cos |
|
(212) |
|||||||
|
|
|
Если угол, на который происходит рассеяние, близок к нормали к слою ( |
|||||||||||
|
z |
|
0.999999 ), |
то вместо формул (212) должно быть использовано выражение |
||||||||||
|
|
|||||||||||||
