Кочубей СПЕКТРОСКОПИЯ РАССЕИВАЮЩИХ СРЕД

Уменьшение относительной площади отверстий приводит к существенному увеличению коэффициента умножения сферы. Для относительной площади отверстий, большей 0.05, потери начинают превышать преимущества, которые дает высокий коэффициент отражения покрытия сферы. Таким образом, площадь открытых портов не должны превышать 5% площади сферы.

Реальные сферы изготавливаются с учетом диаметров отверстий. При этом размер отверстий обусловлен как размерами устройств, для которых эти отверстия изготавливаются, так и геометрией самой сферы.

Рассмотрим случай наличия двух отверстий единичного диаметра. Для относительной силы света можно записать:

Как правило, меньшие сферы обеспечивают большую яркость. Однако, т.к. интегрирующая сфера обычно используется для пространственного интегрирования светового потока, необходимо увеличивать размер сферы и уменьшать диаметр отверстий. Из рисунка 6 следует, что, для трех сфер с одинаковой величиной входящего светового потока, освещенности одинаковы и максимальны, если коэффициент отражения равен 1. Таким образом, высокое отражение покрытия интегрирующей сферы, например «Spectralon», может оптимизировать пространственные характеристики сферы при небольшом уменьшении освещенности.

Временной отклик интегрирующей сферы

Большинство интегрирующих сфер изготавливается как устройства для измерения стационарных световых потоков. Анализ их работы в большинстве вариантов использования показывает, что уровень освещенности внутри сферы постоянен в течение достаточно длительного времени, поэтому переходная характеристика не принимается во внимание. В случае измерения быстро изменяющегося светового сигнала, например, модулированного с высокой частотой, или коротких импульсов, выходной сигнал может быть значительно искажен вследствие множественных диффузных отражений света. Это приводит к уширению входящего импульса. Профиль выходящего сигнала определяется конволюцией входящего сигнала с переходной характеристикой интегрирующей сферы.

Переходная характеристика имеет форму:

Здесь ρ - усредненный коэффициент отражения стенок сферы; с - скорость света;

19

- диаметр интегрирующей сферы.

Постоянная времени большинства стандартных интегрирующих сфер лежит в диапазоне от нескольких наносекунд до нескольких десятков наносекунд.

Выбор покрытия интегрирующей сферы

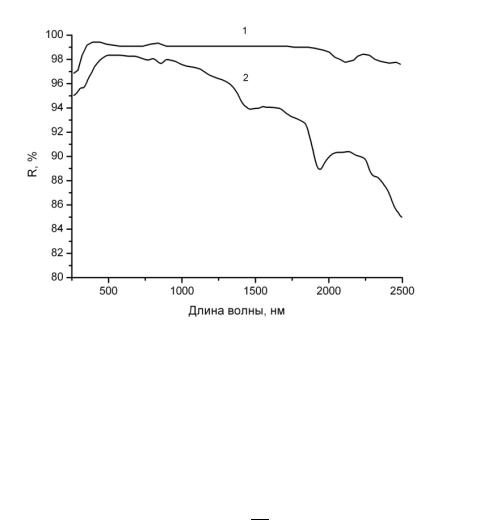
Коэффициент умножения сферы, продемонстрированный на рис 3, сильно зависит от отражения покрытия внутренней поверхности сферы. Выбор материала покрытия может дать существенные различия в яркости, полученной для одной и той же конструкции сферы. Фирмой Labsphere используются два материала покрытий, имеющих торговые марки «Spectraflect» и «Spectralon». Оба покрытия могут использоваться в спектральном диапазоне 250-2500 нм. Спектральная зависимость коэффициентов отражения данных материалов показана на рис. 6.

Рис. 6. Спектральная зависимость коэффициента отражения для покрытий: 1 - «Spectralon», и 2 - «Spectraflect»

Оба покрытия имеют высокий коэффициент отражения, близкий к 95%, в диапазоне 350-1350 нм. Следует отметить, что относительное увеличение яркости больше, чем относительное увеличение коэффициента отражения на величину,

Величина этого эффекта отображена на рисунке 7.

Так как «Spectralon» дает отражение на 2 — 15% больше, чем «Spectraflec» в одинаковом спектральном диапазоне, интегрирующая сфера с покрытием из

20

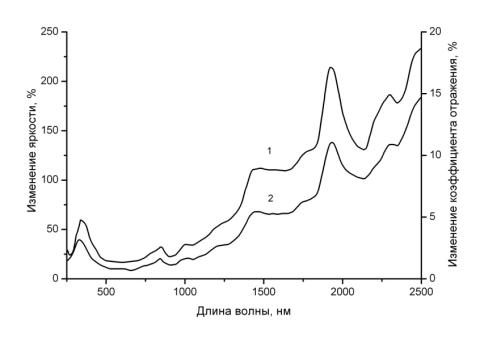
«Spectralon» будет давать силу света на 40 — 240% выше. Большая эффективность имеет место в ближнем ИК диапазоне выше 1400 нм.

Рис. 7. Спектральная зависимость изменения яркости (1) и коэффициента отражения (2) поверхности сферы при замене материала покрытия с

«Spectraflect» на «Spectralon»

Спектроскопия с использованием интегрирующих сфер

При проведении спектральных измерений рассеивающих образцов существенную роль играет тот факт, что получение однородного образца может представлять собой непростую задачу. Влияние возможных артефактов, связанных неоднородностями образцов, изучалось в работе [26].

Среди методов определения оптических свойств сильно рассеивающих неоднородных сред, один из наиболее широко используемых и точных методов - спектральные измерения с использованием интегрирующих сфер. Возможны различные конфигурации проведения измерений отражения и пропускания образца. Прежде всего, существуют два способа освещения образца: диффузный и коллимированный. В работе [24] было показано, что коллимированное освещение образца позволяет точнее определить оптические свойства исследуемой ткани. Однако, в ряде случаев, добиться освещения образца коллимированным излучением не удается, например, при использовании одновременно двух интегрирующих сфер. В этом случае необходим учет прохождения света через образец при диффузном освещении. При использовании двух интегрирующих сфер измерения отражения и пропускания можно осуществлять одновременно, в отличие от применения одной

21

интегрирующей сферы. В этом случае измерения проводят последовательно. Погрешности при измерениях неизбежны в обоих случаях. Так, например, при измерениях с одной интегрирующей сферой, при исследовании неоднородных образцов могут возникать ошибки из-за того, что отражение и пропускание измеряются для несколько разных участков образца. Это происходит вследствие того, что, при последовательных измерениях, необходимо менять положение образца относительно сферы: при измерении пропускания образец помещается перед входным отверстием, для измерения отражения – после выходного отверстия. В случае одновременных измерений с двумя интегрирующими сферами необходимо принимать во внимание тот факт, что, что часть света, прошедшего через образец во вторую сферу, может вернуться в первую сферу и наоборот. Таким образом, оказывается необходимым учет взаимодействия сфер [24, 25]. Выбор конкретной конфигурации эксперимента определяется, как правило, физическими свойствами образца и требованиями, предъявляемыми к получаемым результатам. Например, при определении оптических свойств образцов, меняющих свое состояние во времени (суспензий живых клеток или крови, же динамически просветляемых образцов, исследования протекания химических реакций), время, затрачиваемое на проведение измерений, является очень важным фактором. Поэтому измерения желательно проводить на спектрофотометре с двумя интегрирующими сферами [27-29]. Если же определяются оптические свойства однородного и стабильного образца с сильно анизотропным рассеянием, то предпочтительнее проводить измерения на спектрофотометре с одной интегрирующей сферой. При этом можно избежать описанного выше взаимодействия между сферами [30].

Интерпретация величин, измеряемых с помощью интегрирующих сфер, требует применения математической модели распространения оптического излучения в образце. Все современные методы обработки данных измерений с интегрирующей сферой основаны на теории переноса излучения или ее аппроксимациях. Более подробно эти теории будут рассмотрены в последующих разделах.

В ранних работах, [31, 32], использовалось так называемое приближение Кубелки-Мунка. Это приближение основано на представлении поля излучения внутри образца как суммы двух световых потоков, распространяющихся в противоположных направлениях [33]. Последующие исследования выявили ряд недостатков этой модели, в частности: неприменимость к средам с высокой анизотропией рассеяния [33], сложность учета преломляющих границ [34], трудность пересчета параметров Кубелки-Мунка в стандартные параметры теории переноса излучения [32].

Следующей моделью, предложенной для обработки спектров, полученных с помощью интегрирующих сфер, стало диффузионное приближение теории переноса излучения [35, 36]. В этом приближении лучевая интенсивность

22

излучения, распространяющегося в рассеивающей среде, может быть представлена как сумма ослабленной падающей компоненты и диффузной компоненты. Согласно диффузионному приближению, диффузная интенсивность формируется в результате взаимодействия падающего излучения со значительным количеством рассеивающих частиц среды. Вследствие этого ее угловое распределение лишь немного отличается от изотропного:

Диффузионное приближение также не свободно от ограничений. Во-первых, для корректности диффузионного приближения, необходимо выполнение условия, что не всегда справедливо. Во-вторых, диффузионное приближение, строго говоря, может быть использовано лишь на больших расстояниях от

источников и границ. Это условие часто не выполняется для тонких образцов.

В связи с этим, для интерпретации данных, полученных с использованием интегрирующих сфер, было предложено использовать метод сложения-удвоения [39, 40]. Метод сложения-удвоения представляет собой численный метод решения уравнения переноса, свободный от каких-либо предположений об оптических свойствах среды. Параллельно с этим разрабатывались первые версии инверсного метода Монте-Карло [41, 42], т.е. метода, который комбинирует какой-либо (обычно квазиньютоновский) алгоритм решения обратной задачи и метод Монте-Карло для решения прямой задачи. К 1993 году рядом исследователей было осознано еще два фактора, играющих важные роли в интерпретации данных, полученных с использованием интегрирующих сфер. Вопервых, боковые потери света на краях образца могут приводить к завышению определяемого коэффициента поглощения [34, 43, 47]. Во-вторых, вклад рассеянного излучения в измеряемый сигнал коллимированного пропускания может привести к занижению определяемой оптической толщины образца [4345]. Учет боковых потерь требует как минимум двумерной модели распространения излучения в среде. Реализация учета боковых потерь в рамках метода сложения-удвоения представляет собой сложную задачу, поскольку последний является существенно одномерной моделью. В связи с этим были

23

предложены двумерные версии инверсного метода Монте-Карло, явно учитывавшие роль краевых эффектов [46, 47].

С помощью спектрофотометрии с использованием интегрирующих сфер было исследовано огромное количество биотканей [5, 8, 10, 11, 13, 14, 26, 37, 39, 40, 42, 47-49]. Определялись оптические свойства кожи, печени, белого и серого вещества мозга, черепа человека и некоторых других тканей. Однако, результаты различных исследований зачастую противоречат друг другу [39]. Подобные различия можно объяснить различиями в экспериментальных условиях проведения измерений, различиями используемых моделей для определения оптических свойств ткани по данным измерений, а также различиями в приготовлении образцов тканей.

Анализ опубликованных работ по использованию спектрофотометрии интегрирующих сфер для биомедицинских исследований показывает, что, несмотря на широкое использование данного метода, существует ряд проблем, требующих дальнейшей разработки новых и совершенствования имеющихся методов определения оптических свойств.

Рассмотрим варианты практических схем с использованием интегрирующих

сфер.

Спектрофотометр с одной интегрирующей сферой

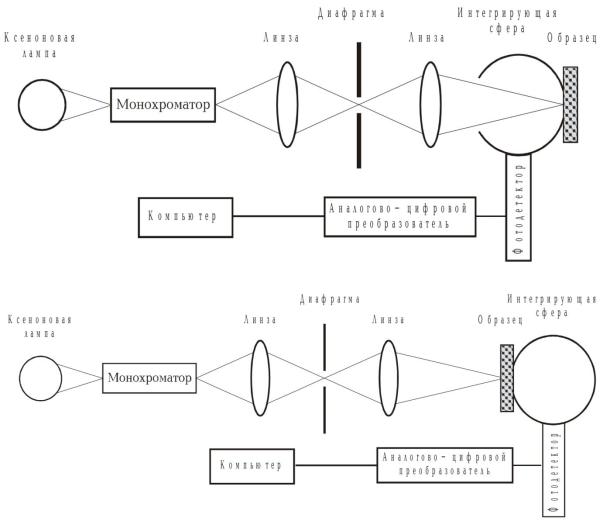
При регистрации спектров с использованием одной интегрирующей сферы необходимо, как отмечалось выше, перемещать образец для того, чтобы получить спектры пропускания, отражения или полного поглощения (рис. 8). Стандартная система включает в себя источник света, монохроматор для выделения требуемого спектрального участка излучения, систему формирования профиля монохроматизированного светового пучка, интегрирующую сферу с встроенным фотоприемником и систему регистрации сигнала.

Как правило, все составляющие представляют собой единую конструкцию спектрофотометра, за исключением интегрирующей сферы – она может быть как встроенной, так и сменной приставкой. На рисунке указано расположение образца при регистрации спектров диффузного отражения (рис. 8, а) и полного пропускания (рис. 8, б). При регистрации полного поглощения образец помещается внутрь, в центре сферы. При использовании интегрирующей сферы одним из нежелательных эффектов является регистрация люминесценции образца. Так как не существует препятствия для попадания данной люминесценции внутрь сферы, люминесценция попадает на фотоприемник и искажает данные о поглощении или отражении. При этом надо учитывать, что, вследствие того, что пространственный угол сбора люминесценции составляет практически 2π, величина ее вклада в регистрируемый сигнал может быть очень большой.

24

а

б

Рис. 8. Схема эксперимента для регистрации спектров рассеивающих образцов при использовании одной интегрирующей сферы:

а) измерение диффузного отражения; б) измерение полного пропускания

Для исследования динамики процессов бывает необходимо одновременное измерение отражения и пропускания образца. Для корректного проведения подобных экспериментов был предложен метод двух интегрирующих сфер. При таком эксперименте образец помещается между двумя сферами (рис. 9), соответственно возникает необходимость дополнительных коррекций измеряемых величин, обусловленная паразитным обменом оптического излучения между двумя сферами [24, 25]. Несмотря на это, метод двух интегрирующих сфер приобрел значительную популярность в последние несколько лет [47-49].

25

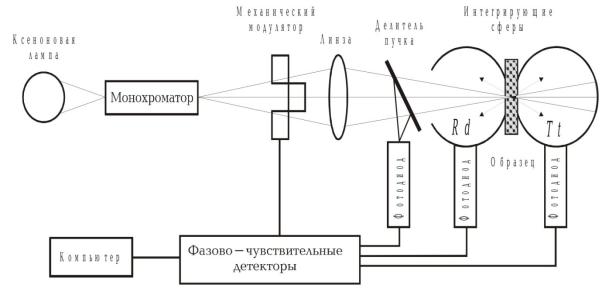
Рис. 9. Схема спектрофотометра с двумя интегрирующими сферами

Измерение коллимированногопропускания

При исследовании оптических параметров рассеивающих образцов необходимо определение трех величин: коэффициента поглощения света образцом а, коэффициента рассеяния s и среднего косинуса угла рассеяния, т.е. фактора анизотропии g. Для корректного определения трех величин необходимы три независимых измерения, при этом вид этих измерений определяется исследователем. Чаще всего происходит выбор из: диффузного отражения; полного пропускания, включающего в себя как диффузную, так и коллимированную компоненту прошедшего света; диффузного пропускания; полного поглощения или коллимированного пропускания Tc.

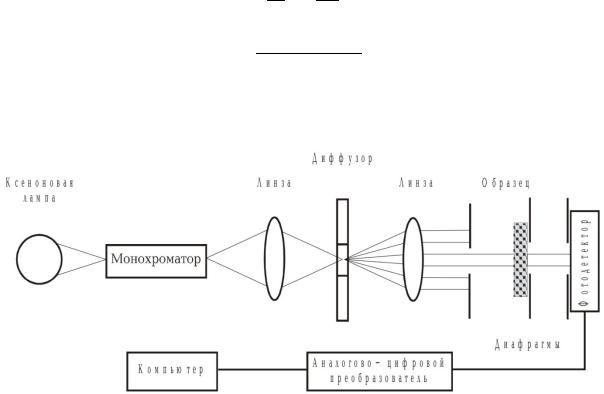
Измерение коллимированного пропускания проводится по схеме, приведенной на рис. 10. Монохроматизированное излучение фокусируется на оптическом диффузоре (диафрагме), закрепленном в диафрагме для создания точечного источника света. Это позволяет высокую степень коллимации при помощи линзы освещающего образец света. После этого, при помощи системы диафрагм, выделяется узкий пучок прошедшего через образец света. Система диафрагм применяется для уменьшения вклада рассеянного излучения в измеряемый сигнал. В приведенном примере использовались две диафрагмы. Одна из них располагается сразу после образца, а другая на некотором расстоянии от первой, непосредственно перед детектором.

Одним из важных параметров, позволяющих минимизировать ошибку при измерении коллимированного пропускания, является толщина исследуемого образца. Измерение достаточно толстого образца приводит к попаданию на фотоприемник диффузной компоненты прямо прошедшего излучения и соответствующему занижению коэффициента рассеяния. Как было показано в

26

работе [50] максимальная толщина, которая может быть использована для корректного измерения коллимированного пропускания, определяется выражением

[ 2 ln .

где d – диаметр падающего на образец луча, λ – длина волны, при условии

3 ( + ),

которое обычно выполняется для биологических тканей в видимом и ближнем ИК спектральном диапазоне длин волн.

Рис. 10. Экспериментальная установка для измерения коллимированного пропускания

Влияние кюветы на измеренные данные

При использовании кюветы возникают некоторые трудности, связанные с тем, что световой пучок, проходящий через нее, не коллимирован. В результате, при расчете оптических характеристик образца, и транспорта света через образец, надо учитывать преломление и отражение света на стенках кюветы. В зависимости от того, какая среда исследуется – слабо рассеивающая, или сильно рассеивающая, получают разные значения интенсивности прошедшего света. Так как, например, при исследовании сильно рассеивающей среды, отклонения направления распространения лучей от нормали к стенке кюветы вследствие рассеивания света могут быть значительны, угол падения света на заднюю стенку кюветы может стать больше угла полного внутреннего отражения. Вследствие этого часть прошедшего через образец излучения будет потеряна из рассмотрения, отразившись обратно в кювету. Следовательно, даже если при измерении сильно рассеивающего образца используется интегрирующая сфера, измеренное значение коэффициента пропускания света не будет соответствовать характеристикам среды.

27

РАСЧЕТ ПРОХОЖДЕНИЯ СВЕТА ЧЕРЕЗ РАССЕИВАЮЩУЮ СРЕДУ

Световое излучение при взаимодействии с пространственно неоднородным рассеивающим образцом может отражаться, поглощаться, рассеиваться и переизлучаться. Таким образом, получение точных данных об оптических свойствах рассеивающего образца представляет собой сложную задачу ввиду одновременного протекания нескольких процессов, зависящих от свойств самого образца (оптических параметров, геометрической конфигурации, размеров) и от свойств падающего на образец света (длины волны, форму светового пучка, степени его расходимости). В то же время знание оптических свойств очень важно. Например, для биологических тканей оно важно для фотодинамической терапии и методов диагностики различных заболеваний [51].

При рассмотрении рассеяния фотонов стоит учитывать направление отклонения траектории фотона после взаимодействия с рассеивающим объектом. Анизотропия рассеяния g описывает средний угол отклонения фотона для единичного акта рассеяния. Параметр g определяется как среднее значение косинуса угла отклонения: g <cos >. Если угол является совершенно случайной величиной (изотропное рассеяние, g=0), то единичный акт рассеяния будет приводить фотон к полной потере его первоначального направления движения в среде. В этом случае фотон будет двигаться в пределах среды хаотично, с длиной свободного пробега 1/μs между актами рассеяния. В тканях, однако, угол отклонения обычно незначителен (например, между 50 и 450) и, фотон продолжает свое движение вперед с малым отклонением. Фотону требуется испытать приблизительно 1/(1-g) актов рассеивания, пока он потеряет первоначальное направление движения в ткани, затем фотон движется хаотически, с длиной свободного пробега хаотического движения 1/(μs(1-g)). Длина свободного пробега хаотического движения фотонов очень важна в определении бокового распространения и глубины проникновения света в биоткань.

Обычно, оптические свойства получают, решая уравнения переноса излучения [52]. В зависимости от метода, решения являются точными или приближенными. Методы определения оптических параметров рассеивающих образцов можно условно разделить на два класса: прямые и непрямые (косвенные). Прямые методы имеют строгие ограничения на свойства используемого в эксперименте образца, для того чтобы согласовать условия эксперимента с предположениями, сделанными для получения точного решения. Например, прямой метод, используемый Flock и др. [53] требует очень тонких образцов, в которых многократное рассеяние игнорируется. В прямых методах оптические свойства определяются фактически на основании закона Бугера-Бера. Прямыми методами являются, например, измерения пропускания без рассеяния,

28