Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный университет информационных технологий, механики и оптики

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Кочубей СПЕКТРОСКОПИЯ РАССЕИВАЮЩИХ СРЕД

.pdf

Скачиваний:

126

Добавлен:

21.03.2016

Размер:

2.19 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 107 8 9 10 > Следующая >>>

Преобразование уравнения (83) в безразмерную форму требует замены цилиндрических координат z и r безразмерными переменными z a s иr a s . В результате диффузионное уравнение может быть записано в цилиндрической системе координат в следующей форме:

2 d r

1 a 1 ag d r S

(131)

где член источника S r выражается соотношением (132):

3 1 r

a 1 g 1 a

(132)

При использовании граничных условий необходимо также выразить

параметры h и Q r в безразмерной форме.

3 1 ga

(133)

Q r 3hga 1 rs F0 e .

(134)

Необходимо также отметить, что выражение для потока диффузной

компоненты излучения, получаемое из уравнения (81), а именно

Fd r

g s

1 rs F0

exp t z z

3 tr

(135)

в безразмерной форме имеет вид:

Fd r

h d

h d r

3ga 1 rs

F0 e

(136)

Решение одномерного диффузионного уравнения

Одномерное диффузионное уравнение в безразмерной форме определяется выражением (137).


	d2 d		kd2 d S
				(137)
	d 2	,
где S и kd2 определяются выражениями (138) и (139).
S 3a 1 g 1 a 1 rs F0e .				(138)
	kd2	3 1 a 1 ga .		(139)

Уравнение (137) это обыкновенное неоднородное дифференциальное уравнение 2-го порядка. Его решение представляет собой сумму общего решения соответствующего однородного дифференциального уравнения и частного решения неоднородного уравнения.

Частное решение данного неоднородного уравнения имеет форму

dpart c3e	(140)
,

где коэффициент c3 определяется как:

3			a 1 g 1 a 1 rs F0
c3
c3	1 kd2					,	(141)
или в размерной форме:
c		3 s tr t g		1 r	F
c				1 r	F
3			t2 kd2	s	0 .		(142)
Общее решение соответствующего однородного дифференциального
уравнения имеет вид
dhomo c1 exp kd c2 exp kd						,	(143)
						,	(143)

где коэффициенты с1 и с2 определяются граничными условиями. Так, например, для сильно рассеивающей среды, имеющей геометрию бесконечного слоя конечной толщины, получим систему уравнений (144).

	1	Atophkd c2 1 Atophkd AtopQ 0 c3 1 Atoph
c1
	1	Abottomhkd ekd c2 1 Abottomhkd e kd AbottomQ c3	1 Abottomh e
c1
			(144)
Решение	системы уравнений (144) позволяет найти искомые значения

коэффициентов с1 и с2. В случае полубесконечной среды коэффициент с1 обращается в нуль, а коэффициент с2 (в случае несогласования показателей преломления среды и ее окружения) выражается уравнением (145).

AtopQ 0 c3 1 Atoph

1 Atophkd

(145)

Полное решение неоднородного дифференциального уравнения (137)

выражается как:

d c1ekd c2e kd c3e

(146)

Диффузный поток излучения, через единицу площади, определяется

уравнением (136). Проекция этого потока на ось Z определяется выражением

(147).

d d

3ga 1 r

F e

(147)

Коэффициенты диффузного отражения Rd и пропускания Td

слоя сильно

рассеивающей среды определяются уравнениями (148) и (149).

Fd z

1 rs

(148)

Fd z

1 rs

(149)

Для среды, имеющей геометрию бесконечного слоя конечной толщины, освещаемой коллимированным светом, коэффициенты диффузного отражения и пропускания имеют вид:

kdc2

kdc1

3hga 1 rs

2 F

(150)

kdc2e kd kdc1ekd c3e

3hga 1 rs

2 F

(151)

Количество энергии (Вт/см3), поглощенной на глубине , определяется

соотношением (152).

dFd

dFcoll

dz .

(152)

Учитывая, что Fcoll

Icoll

r,s

s d

, и

подставляя в уравнение

(152)

уравнение (80), формулу (152) можно переписать в форме (153).

A a d 1 rs F0 exp .

(153)

Трехмерное решение диффузионногоуравнения

Рассмотрим трехмерное решение диффузионного уравнения (154) для случая бесконечного слоя конечной толщины, освещаемого по нормали к поверхности коллимированным источником света с граничными условиями (1.55)

и (156).

	2 d r				kd2 d r S r			,		(154)
где S r 3a 1 g 1 a 1 rs F0 e								,		(154)
где S r 3a 1 g 1 a 1 rs F0 e				и kd2			3 1 a 1 ga .
		d r
d r Atoph						AtopQ r ,			0
d r Atoph						AtopQ r ,			0	(155)
									,	(155)
d r	Abottomh		d r				AbottomQ r ,
d r	Abottomh						AbottomQ r ,			(156)
где Q r 3hga 1 rs F0 e .									,	(156)
где Q r 3hga 1 rs F0 e .
Пусть G r,r есть функция Грина							(157) для		однородного	уравнения

Гельмгольца с соответствующими однородными смешанными граничными условиями (158) и (159).

2G r,r kd2G r,r r r

(157)

G r,r Atoph

G r,r

(158)

G r,r Abottomh

G r,r

(159)

Решение уравнений (154)-(156) может быть найдено с помощью формулы

Грина:

v v

(160)

volume

surface

Здесь n - внешняя нормаль к поверхности, окружающей объем, по которому производится интегрирование в левой части уравнения (160). Если u G r,r и v d r , то уравнение (160) может быть преобразовано к виду (161).

G r,r 2 d r d r 2G r,r dV

volume

G r,r

d r

surface

(161)

Добавляя и вычитая G r,r kd2 d r

из левой части уравнения (161) получаем:

G r,r 2 d r d r 2G r,r dV

volume

G r,r

d r

kd d

d r

kdG r,r

dV .

volume

(162)

Используем уравнения (154) и (157) для упрощения уравнения (162)

G r,r 2 d r d r 2G r,r dV

G r,r S r dV d r

volume

.(163)

Поверхностный интеграл в уравнении (160) может быть переписан при

использовании условия, что на верхней поверхности слоя

(164)

и на нижней поверхности

(165)

Поскольку возрастает с глубиной в слое, и n есть внешняя нормаль к поверхности слоя. При подстановке уравнений (164) и (165) в правую часть уравнения (161) получаем:

d r

G r,r

surface

d r

G r,r

d r

G r,r

d r

dS .

(166)

Это уравнение может быть упрощено использованием граничных условий

(155), (156), (158), (159).

d r

G r,r

surface

G r,r

Q r

G r,r

Q r

(167)

Сравнение уравнений (163) и (167) позволяет получить выражение, определяющее d r , в терминах функции Грина G r,r .

G r,r

Q r

d r G r,r S r dV

G r,r

Q r

volume

(168)

Функция Грина в цилиндрической системе координат, с

r и r ,

выраженными в , , координатах, имеет вид:

G r,r

n I0 n

n 1

2 Nn

(169)

где K0 и I0 модифицированные функции Бесселя, и Zn

собственные функции,

удовлетворяющие дифференциальному уравнению (157)

sin kn n

(170)

Собственные значения

могут

быть получены подстановкой

функции

Грина в граничные условия при 0.

tg n Atophkn

(171)

Собственные значения kn

могут быть получены наложением на функцию

Грина граничных условий (159) при .

tg kn n Abottomhkn

(172)

Использование уравнения (171) позволяет упростить выражение (172)

tg k

Atop

Abottom hkn

Atop Abottom hkn

(173)

Нормировочный множитель N2

может быть получен с помощью выражения

(174)

sin 2 n sin 2 kn n 2kn

Nn2

4kn

(174)

Окончательно, подставляя функцию Грина (169) в диффузионное уравнение

(157), получаем соотношение между n и kn :

2 k2

(175)

d .

Решение диффузионного уравнения определяется уравнением (168). Подставляя функцию Грина в объемный интеграл в правой части уравнения (168) получаем

sin k

G r,r S r dV

(176)

volume

n 1

n ,

где

(177)

zn sin n 1 e

kn sin kn cos kn

cos n kn

sin kn kn cos kn

и радиальный член Bn

определяется как

Bn K0 n F0 I0 n n d n

0 n

(178)

Радиальный член Bn определяется источником излучения. Если источник

излучения представляет собой луч конечной ширины

0 ,

который образован

плоской волной, то:

	0		n 0			I	0	n			1	n	0
F		1									K
Bn	0		n 0	K	0			n	I	1	n	0

F

Если 0 , то уравнение (179) преобразуется как

Bn F0 .

Радиальный член для импульсного источника локализованного в центре:

0
0	(179)
	(179)

(180) (т.е. дельта-функция),

Bn F0K0 n

(181)

Использование луча с Гауссовым профилем радиуса 0 требует, что бы

радиальный член

рассчитывался численно с использованием уравнения

(178) и

e 2 0 2

F0 F0

0 .

(182)

Поверхностные интегралы в уравнении (168) могут быть рассчитаны с

использованием выражений (183) и (184).

Q0 sin kn n sin n Bn

G r,r Q r dS

2 2

(183)

n 1

Nn n

Q0 sin kn n sin kn n Bn e

G r,r Q r dS

2 2

n 1

Nn n

(184)

Использование уравнений (176), (183) и (184) позволяет записать решение

диффузионного уравнения в виде

sin k

Q sin

d r

2 2

n 1

Nn n

. (185)

Выпишем частные производные функции d

по и .

cos k

Q sin

Q sin k

2 2

n 1

Nn n

(186)

sin k

Q sin

Q sin k

n 1

(187)

Поток излучения в точке с радиус-вектором r описывается уравнением

Fd r	h d r		h d r	3ga 1 rs F0 e
		r			z

	2	2			.

Уравнения (186) и (187) позволяют рассчитать эту величину в случае решения трехмерной задачи (в цилиндрической системе координат). Коэффициенты диффузного отражения и пропускания и в этом случае будут рассчитываться по формулам (148) и (149), с учетом того, что входящие в них величины являются функцией радиуса падающего луча и F0 - полная мощность излучения падающего на среду.

R		Fd r z
R		1 rs F0
d		1 rs F0	0	(188)
T		Fd r z	0


	1 rs F0
d
				(189)
				(189)

Решение уравнения переноса излучения методом "добавления-удвоения"

Вслучае простой геометрии исследуемой среды и эксперимента, существует возможность строгого решения уравнения переноса излучения, в случае как сильно, так и слабо рассеивающих сред. Для получения строгого решения можно использовать, например метод дискретных ординат, метод X и Y функций Чандрасекара или метод "добавления-удвоения" (ДУ) ("adding-doubling" метод). Метод ДУ имеет следующие преимущества: (1) требует минимального количества машинного времени, т.е. позволяет быстро производить вычисления,

(2)физическая интерпретация результатов может быть выполнена на каждом шаге, и (3) данный метод является эквивалентным для изотропного и анизотропного рассеяния (при этом не накладываются какие-либо ограничения на выбор фазовой функции).

При использовании данного метода необходимо сделать следующие предположения относительно уравнения переноса излучения и геометрии среды и эксперимента: уравнение переноса записывается в форме, не зависящей от времени; геометрия образца состоит из однородных плоскопараллельных бесконечных слоев конечной толщины; каждый слой имеет однородные рассеивающие и поглощающие свойства; поверхность образца равномерно освещается неполяризованным коллимированным или диффузным светом и образец не должен иметь внутренних источников излучения.

Восновном эти предположения ограничивают тип и форму образцов биоткани, но не противоречат известному характеру распространения света в биотканях. В настоящее время метод ДУ широко используется для решения большого числа проблем оптики биотканей.

Термин "удвоение" в названии данного метода означает, что предполагаемые известными (для всех углов, при которых происходит падение и выход лучей из слоя) коэффициенты отражения и пропускания одного слоя могут быть использованы для нахождения коэффициентов отражения и пропускания слоя вдвое большей толщины, путем наложения друг на друга двух идентичных слоев и сложения вкладов в отражение и пропускание от каждого из слоев. Отражение и пропускание слоя произвольной толщины рассчитывается последовательно, сначала для тонкого слоя с теми же оптическими характеристиками (однократное рассеяние), а затем путем последовательного удвоения толщины рассчитываются характеристики слоя требуемой толщины. Методика "удвоения" была предложена ван де Хюлстом для решения уравнения переноса излучения для рассеивающих сред, имеющих геометрию бесконечного слоя конечной толщины.

Термин "добавление" означает распространение методики "удвоения" на образцы с разнородными слоями, что позволяет моделировать многослойные биоткани и учитывать внутреннее отражение за счет скачков показателя преломления на границах слоев.

В тоже время метод ДУ, так же как и диффузионное приближение, не свободен от недостатков. Недостатками метода ДУ являются: невозможность расчета распределения излучения внутри исследуемой среды; ограничения, накладываемые на геометрию образца, заключающиеся в том, что образец должен иметь геометрию равномерно освещенного бесконечного слоя конечной толщины и необходимость, чтобы каждый слой был однороден по своим оптическим свойствам. Одним из основных недостатков данного метода является то, что при использовании его в качестве метода решения прямой задачи при решении обратных задач для интерпретации данных спектрофотометрии с использованием интегрирующих сфер, вследствие своей одномерности метод ДУ не учитывает потерь света на краях образца, что неизбежно приводит к завышению коэффициента поглощения исследуемого образца биоткани. Однако, данное ограничение становится существенным только в случае, когда для исследования используются сравнительно небольшие, по сравнению с размерами луча падающего на образец излучения, образцы биотканей.

Несмотря на ограничения, которые метод ДУ накладывает на геометрию образца, он весьма пригоден для итеративных вычислений, поскольку он обеспечивает точное вычисление коэффициентов диффузного отражения и полного пропускания образца, при сравнительно малых затратах машинного времени. Кроме того, его главным преимуществом перед диффузионным приближением теории переноса излучения, которое так же обеспечивает быстрое проведение расчетов коэффициентов диффузного отражения и полного пропускания в слоевой геометрии, является то, что соотношение коэффициентов поглощения и рассеяния исследуемой среды может быть практически любым, что

позволяет выполнять расчеты не только для сильно, но и для слабо рассеивающих сред с сильным поглощением.

Определение операторов отражения и пропускания

Прежде чем перейти к описанию метода ДУ необходимо ввести понятие операторов отражения и пропускания единичного слоя рассеивающей среды.

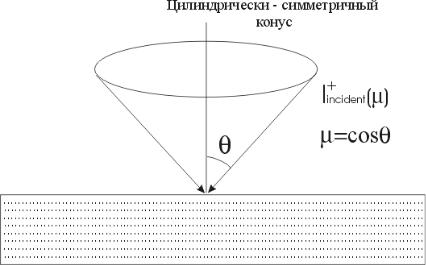
Поскольку метод ДУ подразумевает азимутальную симметрию, то направление распространения световых лучей определяется углами, которые они образуют с нормалью к поверхности образца. Мы будем использовать выражение cos для определения направления распространения луча. Здесьэто направляющий косинус, а это угол, образуемый падающим лучом и нормалью к поверхности среды (Рис. 20).

Конус света, характеризуемый углом , падающий на произвольный рассеивающий слой биоткани, будет частично отражаться от слоя и частично проходить через слой. При этом доли отраженного и прошедшего излучения определяются углом падения.

Определим интенсивность падающего излучения, которое является функцией угла падения , как Iinc , где знак "+" показывает, что излучение

распространяется по направлению сверху вниз. Интенсивность излучения, прошедшего через образец, и образовавшего на выходе конус, направляющая которого образует с нормалью угол , будет определяться зависимостью:

			1		Iinc
		It T ,			Iinc	2 d
			0			.	(190)
Полная интенсивность отраженного от образца излучения будет
определяться как:
			1
		Ir R , Iinc 2 d					(191)
			0			.	(191)
Операторы T ,		и R	,	могут быть записаны в матричной форме,

т.е. как Tij T i, j	и Rij R		i, j , где углы			i и j выбираются исходя из

конкретной квадратурной схемы интегрирования. Индексы i и j показывают элементы матриц T и R. Исходя из этого, интенсивности I и I , могут

быть записаны как вектора Ii I i .

В общем виде уравнения (191) и (192) могут быть представлены как:

A , B , 2 d Aij 2 jwjBjk

0 j ,

где i это j-ый квадратурный угол и wj соответствующи й ему вес. Подробно

квадратурные схемы интегрирования рассмотрены в работе [33]. Единичная матрица E (необходимая нам для дальнейшего рассмотрения) в этом случае

будет иметь вид: Eij	1	ij	, где	ij	- дельта-функция Кронекера.	ij	1 если
	2 w

	i i

i j, и ij 0 если i j .

Рис. 20 Конус света, падающий на поверхность рассеивающей среды

Отметим, что в случае, когда слой освещается коллимированным источником света, диффузное отражение и пропускание слоя будут определяться как:

Rd	1	1R ,	1	2 d 2 d	1	R 1, 2 d
			2
	0					,
	0				0

Td T 1, 2 d

0 .

В случае, когда поверхность слоя освещается диффузным источником света:

1
Rd 01R , 2 d 2 d	,
0	,
1
Td 01T , 2 d 2 d	.
0	.
Фазовая функция рассеяния
Фазовая функция акта единичного рассеяния		света в биотканях
Фазовая функция акта единичного рассеяния	p	света в биотканях

определяет количество света, рассеянного на угол от направления падающего

<<< < Предыдущая 1 2 3 4 5 67 / 107 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
28.09.20198.4 Mб58Копия 3_1isp.doc
#
05.09.2019105.98 Кб10Коренной перелом1.doc
#
26.09.20194.81 Mб2Коробейников_НКМ.doc
#
20.03.201687.04 Кб10Корпоративные финансы_задание.doc
#
08.08.2019128.03 Кб3Кочелаев_сессия.docx
#
21.03.20162.19 Mб126Кочубей СПЕКТРОСКОПИЯ РАССЕИВАЮЩИХ СРЕД.pdf
#
16.08.201913.67 Mб27КР_ИСТПП.doc
#
14.04.2015112.04 Кб4кризис.docx
#
21.03.20166.52 Mб7Крылов - Басни - 1947.pdf
#
14.04.201582.84 Кб18КСЕ семинар 2.docx
#
17.09.2019259.58 Кб2Кто знает причину болезней.doc