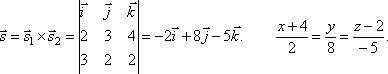Векторное уравнение прямой в пространстве

Пусть для прямой известны ее направляющий вектори точка, лежащая на этой прямой. Пусть-- произвольная (текущая) точка прямой. Обозначим черезиr радиус-векторы точек исоответственно (рис. 11.11).

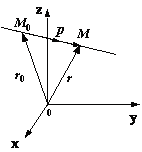
Рис.11.11.Векторное уравнение прямой

Тогда вектор коллинеарен векторуp и, следовательно, , где-- некоторое число. Из рис. 11.11 видно, что

(11.12)

Это уравнение называется векторным уравнением прямой или уравнением в векторной форме. При каждом значении параметра мы будем получать новую точкуна прямой.

Общие уравнения прямой в пространстве

Линия в трехмерном пространстве определяется, вообще говоря, пересечением двух поверхностей, т.е. описывается системой двух уравнений.

Прямую в пространстве можно рассматривать как линию пересечения двух плоскостей и, следовательно, описывать системой двух линейных уравнений

	м н о	A1x + B1y + C1z + D1 = 0 A2x + B2y + C2z + D2 = 0

при условии, что эти плоскости непараллельны, т.е. их нормальные векторы неколлинеарны.

Расстояние между скрещивающимися прямыми в пространстве

• В трехмерном пространстве в прямоугольной системе координат Oxyz заданы две скрещивающиеся прямые a и b. Прямую a определяют параметрические уравнения прямой в пространствевида

X=-2

Y=2t+1

Z=-3t+4

 , а прямую b – канонические уравнения прямой в пространстве. Найдите расстояние между заданными скрещивающимися прямыми.

Очевидно, прямая a проходит через точку и имеет направляющий вектор. Прямая b проходит через точку, а ее направляющим вектором является вектор.

Вычислим векторное произведение векторов и:

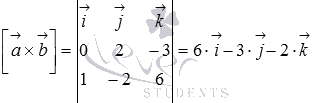
Таким образом, нормальный вектор 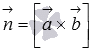плоскости, проходящей через прямую b параллельно прямой a, имеет координаты.

Тогда уравнение плоскости есть уравнение плоскости, проходящей через точкуи имеющей нормальный вектор:

Нормирующий множитель для общего уравнения плоскости равен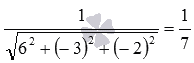. Следовательно, нормальное уравнение этой плоскости имеет вид.

Осталось воспользоваться формулой для вычисления расстояния от точки до плоскости:

Это и есть искомое расстояние между заданными скрещивающимися прямыми.

УГОЛ МЕЖДУ ПРЯМЫМИ

Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.

Пусть в пространстве заданы две прямые:

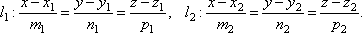
Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами и. Так как, то по формуле для косинуса угла между векторами получим

.

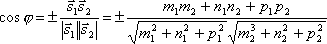Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов и:

Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, т.е. l₁ параллельна l₂ тогда и только тогда, когда параллелен.

Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю: .

Примеры.

1. Найти угол между прямыми 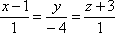и.

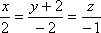2. Найти уравнения прямой проходящей через точку М₁(1;2;3) параллельно прямой l₁:

Поскольку искомая прямая l параллельна l₁, то в качестве направляющего вектора искомой прямой l можно взять направляющий вектор прямой l₁.

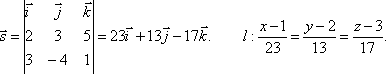
3. Составить уравнения прямой, проходящей через точку М₁(-4;0;2) и перпендикулярной прямым: 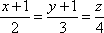и.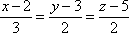

Направляющий вектор прямой l можно найти как векторное произведение векторов и: