
- •2.1Свойства операций над векторами.
- •2,2 Линейная зависимость и независимость векторов.
- •Геометрическая интерпретация скалярного произведения.
- •Свойства смешанного произведения:
- •Угол между двумя прямыми
- •Расстояние от точки до прямой
- •Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору
- •Векторное уравнение прямой в пространстве
- •Общие уравнения прямой в пространстве
- •Расстояние от точки до прямой в пространстве – теория, примеры, решения.
- •Первый способ нахождения расстояния от точки до прямой a в пространстве.
- •Второй способ, позволяющий находить расстояние от точки до прямой a в пространстве.
- •Решение задач на нахождение расстояния от заданной точки до заданной прямой в пространстве.
- •Взаимное расположение прямой и плоскости в пространстве.
- •Проекция точки на плоскость
1,1
1-Выбираем самый близкий по модулю к 1 элемент 1 столбца и строку с этим элементом ставим на первое место
2-При помощи элементарных преобразований типа 1 добиваемся, чтобы все элементы 1 столбца, начиная со 2 элемента обратились в 0
3-Мысленно вычеркнуть 1 строку и 1 столбец и к полученной матрицы меньшего размера применить шаг 1 данного алгоритма
ранг матрицы – это максимальное количество линейно независимых строк.
2
Итак, метод Гаусса (или, иначе, метод последовательного исключения неизвестных) состоит в следующем:
Путем элементарных преобразований систему уравнений приводят к эквивалентной ей системе с верхне-треугольной матрицей. Эти действия называют прямым ходом.
Из полученной треугольной системы переменные находят с помощью последовательных подстановок (обратный ход).
При этом все преобразования проводятся над так называемой расширенной матрицей системы, которую и приводят к верхнее - треугольному виду в прямом ходе метода.
система имеет бесчисленное множество решений, так как ранг матрицы меньше числа неизвестных.
что ранги основной и расширенной матриц равны 4, причем ранг совпадает с числом неизвестных, следовательно, система имеет единственное решение:
1,2
|
|
x1-2/5+(-3/5)
= 0,
x1-5/5
= 0,
x1 =
5/5 = 1.
Проверка:
|
1,3
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.
Необходимость
Пусть система совместна.
Тогда существуют числа ![]() такие,
что
такие,
что![]() .
Следовательно, столбец
.
Следовательно, столбец![]() является
линейной комбинацией столбцов
является
линейной комбинацией столбцов![]() матрицы
матрицы![]() .
Из того, что ранг матрицы не изменится,
если из системы его строк (столбцов)
вычеркнуть или приписать строку
(столбец), которая является линейной
комбинацией других строк (столбцов)
следует, что
.
Из того, что ранг матрицы не изменится,
если из системы его строк (столбцов)
вычеркнуть или приписать строку
(столбец), которая является линейной
комбинацией других строк (столбцов)
следует, что![]() .
.
Достаточность
Пусть ![]() .
Возьмем в матрице
.
Возьмем в матрице![]() какой-нибудь
базисный минор. Так как
какой-нибудь
базисный минор. Так как![]() ,
то он же и будет базисным минором и
матрицы
,
то он же и будет базисным минором и
матрицы![]() .
Тогда, согласно теореме о базисномминоре,
последний столбец матрицы
.
Тогда, согласно теореме о базисномминоре,
последний столбец матрицы ![]() будет
линейной комбинацией базисных столбцов,
то есть столбцов матрицы
будет
линейной комбинацией базисных столбцов,
то есть столбцов матрицы![]() .
Следовательно, столбец свободных членов
системы является линейной комбинацией
столбцов матрицы
.
Следовательно, столбец свободных членов
системы является линейной комбинацией
столбцов матрицы![]() .
.
1,4
При транспонировании квадратной
матрицы её определитель не меняется: ![]()
Общий множитель в строке можно выносить за знак определителя.
Если две строки определителя поменять местами, то определитель поменяет знак.
Определитель с двумя равными строками равен нулю.
Определитель с двумя пропорциональными строками равен нулю.
Определитель, содержащий нулевую строку, равен нулю.
Определитель не изменится, если к какой-то его строке прибавить другую строку, умноженную на некоторое число.
Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.
Определитель –
это некоторое число поставленное в
соответствие квадратной
матрице![]() .
.
Для неквадратных матриц понятие определителя не вводится.
Для
обозначения определителя
квадратной матрицы A будем
пользоваться обозначением ![]() или
или![]() .
.
2.1Свойства операций над векторами.
Итак,
мы определили операцию сложения векторов
и операцию умножения вектора на число.
При этом для любых векторов ![]() и
произвольных действительных чисел
и
произвольных действительных чисел ![]() можно
при помощи геометрических построений
обосновать следующие свойства
операций над векторами.
Некоторые из них очевидны.
можно
при помощи геометрических построений
обосновать следующие свойства
операций над векторами.
Некоторые из них очевидны.
Свойство коммутативности
 .
.
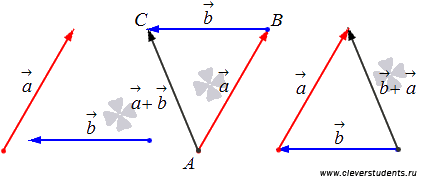
Свойство ассоциативности сложения
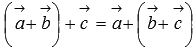 .
.
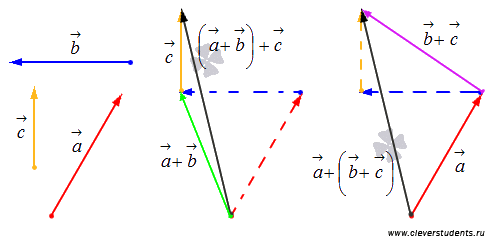
Существует нейтральный элемент по сложению, которым является нулевой вектор
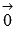 ,
и
,
и  .
Это свойство очевидно.
.
Это свойство очевидно.Для любого ненулевого вектора
 существует
противоположный вектор
существует
противоположный вектор 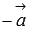 и
верно равенство
и
верно равенство 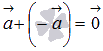 .
Это свойство очевидно без иллюстрации.
.
Это свойство очевидно без иллюстрации.Сочетательное свойство умножения
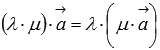 .
К примеру, растяжение вектора в 6 раз
можно произвести, если сначала его
растянуть вдвое и полученный вектор
растянуть еще втрое. Аналогичного
результата можно добиться, например,
сжав вектор вдвое, а полученный вектор
растянуть в 12 раз.
.
К примеру, растяжение вектора в 6 раз
можно произвести, если сначала его
растянуть вдвое и полученный вектор
растянуть еще втрое. Аналогичного
результата можно добиться, например,
сжав вектор вдвое, а полученный вектор
растянуть в 12 раз.Первое распределительное свойство
 .
Это свойство достаточно очевидно.
.
Это свойство достаточно очевидно.Второе распределительное свойство
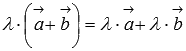 .
Это свойство справедливо в силу подобия
треугольников, изображенных ниже.
.
Это свойство справедливо в силу подобия
треугольников, изображенных ниже.

Нейтральным числом по умножению является единица, то есть,
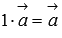 .
При умножении вектора на единицу с ним
не производится никаких геометрических
преобразований.
.
При умножении вектора на единицу с ним
не производится никаких геометрических
преобразований.
Векторное
пространство (линейное
пространство)
- множество элементов, называемых векторами,
для которых определены операции сложения
и умножения на число. Простейший, но
важный пример - совокупность векторов a,
b, c, ...
обычного 3-мерного пространства. Каждый
такой вектор - направленный отрезок,
задаваемый тремя числами: ![]() ;
числа
;
числа![]() называютсякоординатами
вектора.
При умножении вектора на вещественное
число
называютсякоординатами
вектора.
При умножении вектора на вещественное
число ![]() соответствующий
отрезок, сохраняя направление,
растягивается в
соответствующий
отрезок, сохраняя направление,
растягивается в![]() раз:
раз:![]() .
Сумма двух векторов находится поправилу
параллелограмма;
если
.
Сумма двух векторов находится поправилу
параллелограмма;
если ![]() и
и![]() то
то![]() .
Паре векторовa и b сопоставляют
также скалярное
произведение
.
Паре векторовa и b сопоставляют
также скалярное
произведение ![]() (см.Векторная
алгебра).
Непосредственным обобщением З-мерного
пространства является n-мерное евклидово
пространство.
Его элементы - упорядоченные наборы
вещественных чисел, Например,
(см.Векторная
алгебра).
Непосредственным обобщением З-мерного
пространства является n-мерное евклидово
пространство.
Его элементы - упорядоченные наборы
вещественных чисел, Например, ![]() ,
,![]() .
Сложение иумножение
векторов на число определены
формулами
.
Сложение иумножение
векторов на число определены
формулами ![]() ,
,![]() ,
а скалярное произведение - формулой
,
а скалярное произведение - формулой![]() Примером
комплексного бесконечномерного
векторного пространства может служить
совокупность
Примером
комплексного бесконечномерного
векторного пространства может служить
совокупность![]() комплексных
функцийf,
заданных на всей оси
комплексных
функцийf,
заданных на всей оси ![]() и квадратично
суммируемых (то есть имеющих конечный
интеграл
и квадратично
суммируемых (то есть имеющих конечный
интеграл![]() ).
Многие классы функций,
например,полиномы заданного
порядка, функции непрерывные,
дифференцируемые, интегрируемые,
аналитические и тому подобные, также
образуют бесконечномерные векторные
пространства.
).
Многие классы функций,
например,полиномы заданного
порядка, функции непрерывные,
дифференцируемые, интегрируемые,
аналитические и тому подобные, также
образуют бесконечномерные векторные
пространства.
В трёхмерном пространстве понятие «длина вектора» понимается интуитивно как расстояние между его началом и концом. Наиболее важными свойствами «длины вектора» являются следующие:
Длина нуль-вектора,
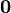 ,
равна нулю; длина любого другого вектора
положительна.
,
равна нулю; длина любого другого вектора
положительна.Умножение вектора на положительное число во столько же раз увеличивает длину вектора.
Действует неравенство треугольника.
Обобщение этих свойств на более абстрактные векторные пространства носит название нормы. Векторное пространство, в котором определена норма, называется нормированным пространством.

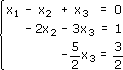 Обратным
ходом метода Гаусса найдем
корни системы. Из последнего уравнения
найдем корень х3:
-5/2x3 =
3/2,
x3 =
(3/2):(-5/2) = 3/2*(-2/5) = -3/5.
Корень
x3 =
-3/5 найден. Подставим его в верхнее
(второе) уравнение системы (-2x2-3x3 =
1):
-2x2-3(-3/5)
= 1,
-2x2+9/5
= 1,
-2x2 =
1-9/5,
-2x2 =
-4/5,
x2 =
(-4/5):(-2) = (-4/5)*(-1/2) = 2/5.
Корень
x2 =
2/5 найден. Подставим его и корень х3 в
верхнее (первое) уравнение системы
(x1-x2+x3 =
0):
Обратным
ходом метода Гаусса найдем
корни системы. Из последнего уравнения
найдем корень х3:
-5/2x3 =
3/2,
x3 =
(3/2):(-5/2) = 3/2*(-2/5) = -3/5.
Корень
x3 =
-3/5 найден. Подставим его в верхнее
(второе) уравнение системы (-2x2-3x3 =
1):
-2x2-3(-3/5)
= 1,
-2x2+9/5
= 1,
-2x2 =
1-9/5,
-2x2 =
-4/5,
x2 =
(-4/5):(-2) = (-4/5)*(-1/2) = 2/5.
Корень
x2 =
2/5 найден. Подставим его и корень х3 в
верхнее (первое) уравнение системы
(x1-x2+x3 =
0):
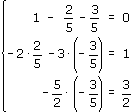 т.
е.
т.
е.
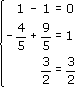 т.
е.
т.
е.