Угол между двумя прямыми

Угол φ между двумя прямыми, заданными общими уравнениями A₁x + B₁y + C₁ = 0 и A₂x + B₂y + C₂ = 0, вычисляется по формуле: 

Угол φ между двумя прямыми, заданными каноническими уравнениями (x-x₁)/m₁ = (y-y₁)/n₁ и (x-x₂)/m₂ = (y-y₂)/n₂, вычисляется по формуле: 

Расстояние от точки до прямой

3,2

Каждую плоскость в пространстве можно представить как линейное уравнение, называемое общим уравнением плоскости

 ,

Частные случаи.

o     Если в уравнении (8) , то плоскость проходит через начало координат.

o     При (,) плоскость параллельна оси(оси, оси) соответственно.

o     При (,)  плоскость параллельна плоскости(плоскости, плоскости).

• Даны точки 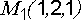,,. Составить уравнение плоскости.

Решение: используем (7)

 

 

 

 

 

  ,    

 

  .

 

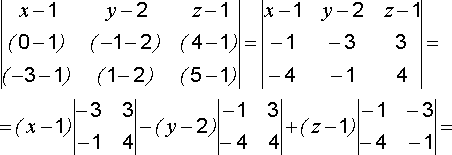
Ответ: общее уравнение плоскости .

• Пример.

Плоскость в прямоугольной системе координат Oxyz задана общим уравнением плоскости . Запишите координаты всех нормальных векторов этой плоскости.

Решение.

Нам известно, что коэффициенты при переменных x, y и z в общем уравнении плоскости являются соответствующими координатами нормального вектора этой плоскости. Следовательно, нормальный вектор заданной плоскостиимеет координаты. Множество всех нормальных векторов можно задать как.

Ответ:

• Пример.

Напишите уравнение плоскости, если в прямоугольной системе координат Oxyz в пространстве она проходит через точку , а- нормальный вектор этой плоскости.

Решение.

Приведем два решения этой задачи.

Из условия имеем . Подставляем эти данные в общее уравнение плоскости, проходящей через точку:

• Пример.

Напишите общее уравнение плоскости параллельной координатной плоскости Oyz и проходящей через точку .

Решение.

Плоскость, которая параллельна координатной плоскости Oyz, может быть задана общим неполным уравнением плоскости вида . Так как точкапринадлежит плоскости по условию, то координаты этой точки должны удовлетворять уравнению плоскости, то есть, должно быть справедливо равенство. Отсюда находим. Таким образом, искомое уравнение имеет вид.

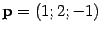• Требуется написать уравнение плоскости, проходящей через точку и параллельной векторам и .

Решение. Векторное произведение по определению 10.26 ортогонально векторам p и q. Следовательно, оно ортогонально искомой плоскости и вектор можно взять в качестве ее нормального вектора. Найдем координаты вектора n:

то есть . Используя формулу (11.1), получим

Раскрыв в этом уравнении скобки, приходим к окончательному ответу.

Ответ: .         

• Найти единичный нормальный вектор плоскости .

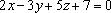Перепишем вектор нормали в виде и найдём его длину:

Согласно вышесказанному:

Ответ: 

• Построить плоскость, проходящую через точку  параллельно плоскости .

У параллельных плоскостей один и тот же вектор нормали. 1) Из уравнения найдём вектор нормали плоскости:.

2) Уравнение плоскости составим по точкеи вектору нормали:

Ответ: 

Векторное уравнение плоскости в пространстве

Параметрическое уравнение плоскости в пространстве

Параметрическое уравнение плоскости

Пусть в координатном пространстве заданы:

а) точка ;

б) два неколлинеарных вектора  (рис.4.15).

Требуется составить параметрическое уравнение вида (4.10) плоскости, компланарной векторам и проходящей через точку

Выберем на плоскости произвольную точку . Обозначим-радиус-векторы точеки(рис.4.16).

Точка принадлежит заданной плоскости тогда и только тогда, когда векторыикомпланарны (см. разд. 1.3.2). Запишем условие компланарности:  где— некоторые действительные числа (параметры). Учитывая, чтополучимвекторное параметрическое уравнение плоскости:

(4.19)

где — направляющие векторы плоскости, а— радиус-вектор точки, принадлежащей плоскости.

Координатная форма записи уравнения (4.19) называется параметрическим уравнением плоскости:

(4.20)

где и— координаты направляющих векторовисоответственно. Параметрыв уравнениях (4.19),(4.20) имеют следующий геометрический смысл: величиныпропорциональны расстоянию от заданной точкидо точкипринадлежащей плоскости. Приточкасовпадает с заданной точкой. При возрастании(или) точкаперемещается в направлении вектора(или), а при убывании(или) — в противоположном направлении.