
10 Линейная регрессия и корреляция результатов измерений
10.1 Основные положения
10.1.1 Области применения
При исследовании работы средств измерений и качества технологических процессов часто необходимо установить взаимосвязь между независимыми переменными и выходным (зависимым) параметром или оценить совместное распределение и взаимосвязь всех измеряемых переменных.
Применение регрессии позволяет оценить или предсказать значение выходного параметра при конкретных значениях контролируемых переменных. Такие задачи решаются при определении функции преобразования средств измерений, при математическом моделировании погрешностей измерений или процессов. Мерой линейной связи между двумя переменными служит корреляция.
10.1.2 Линейная регрессия
10.1.2.1 Однофакторная регрессия
Однофакторная линейная регрессия представляет линейную функцию зависимой переменной у от одной независимой контролируемой переменной х:
у=а+вх (10.1)
Для получения этой регрессии надо вычислить оценки параметров а и в. Уравнение (10.1) определяет прямую линию, пересекающую ось ординат (при х=0) в точке «а» с тангенсом угла наклона к оси абсцисс, равным «в». Таким образом, действительные значения выходного параметра Уj заменяются на модель вида а+вхj . При этом возможно их расхождение (ошибка):
dj=Уj –(а+вхj) (10.2)
Получить параметры модели «а» и «в» можно различными методами. Рассмотрим два из них.
Метод средних предполагает:
- разбиение всех начальных уравнений вида (10.2) на две группы (по числу неизвестных «а» и «в»);
- сложение почленно в каждой группе и приравнивание к 0:
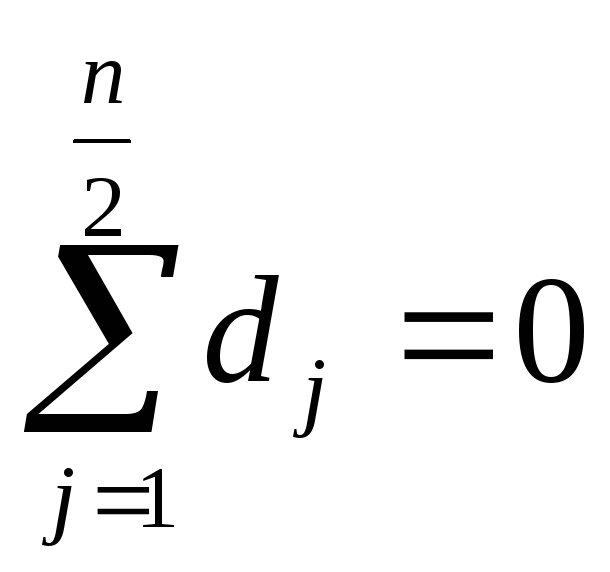
где n число начальных уравнений;
-решение полученных нормальных уравнений относительно «а» и «в».
Недостатком метода является неоднозначность «а» и «в», зависящая от способа группирования начальных уравнений. Более объективным является метод наименьших квадратов (МНК), дающий несмещенные оценки «а» и «в», имеющие минимальные дисперсии. Обязательное условие применения МНК – условное распределение У при данном х должно быть нормальным. Согласно МНК сумма квадратов отклонений действительных и расчетных значений параметра У должна быть минимальна:
![]() (10.4)
(10.4)
Для
минимизации
![]() приравниваем
к нулю частные производные по «а» и «в».
Что даёт:
приравниваем
к нулю частные производные по «а» и «в».
Что даёт:
- производная по «а»:
![]() (10.5)
(10.5)
- производная по «в»:
![]() (10.6)
(10.6)
После упрощений получаем нормальные уравнения:
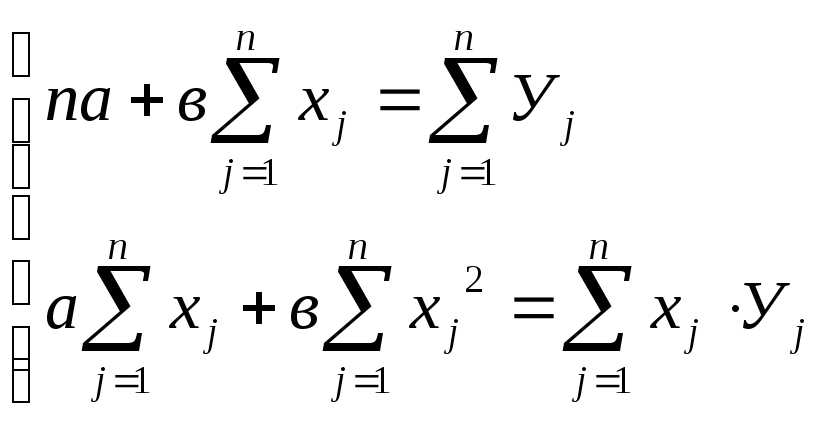 (10.7)
(10.7)
Решая систему уравнений (10.7), получаем:
 (10.8)
(10.8)
![]() (10.9)
(10.9)
После
подстановки
![]() ,
,![]() и преобразований получаем:
и преобразований получаем:
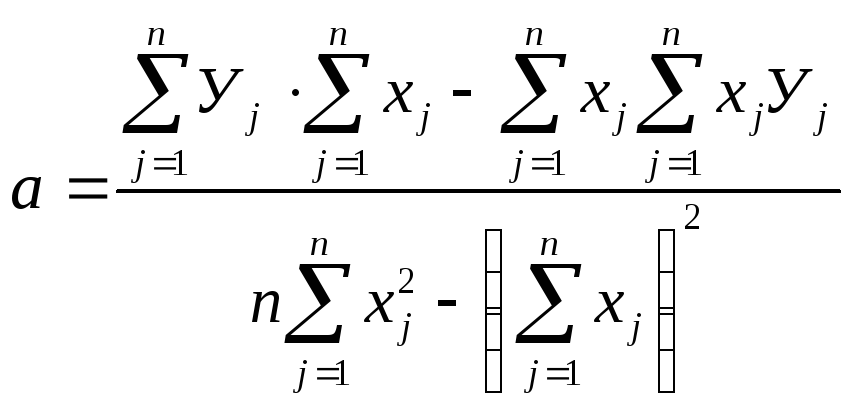 (10.10)
(10.10)
Из
формул (10.8) и (10.10) можно получить формулы,
более удобные при вычислении значений
с большим числом разрядов, умножив
числитель и знаменатель на
![]() :
:
![]() ,
(10.11 )
,
(10.11 )
 (10.12)
(10.12)
МНК можно применять для функций нелинейного вида, которые можно преобразовать в линейные. Заменяющая функция в рассматриваемом случае линейная, называется аппроксимирующей, если получена для аналоговых значений х, и называется интерполирующей для дискретных значений х. Мерой качества аппроксимации (интерполяции) является СКО действительных значений от полученной прямой:
 (10.13)
(10.13)
или формула СКО более удобная для вычислений:
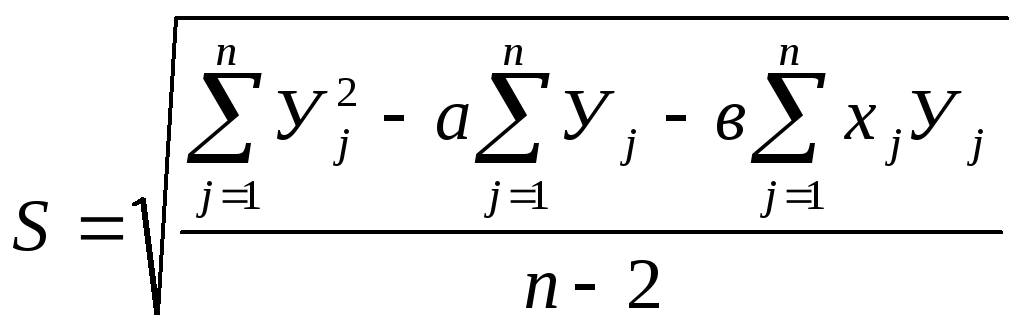 (10.14)
(10.14)
Доверительные интервалы для параметров «а» и «в»:
 <
A
<
<
A
<
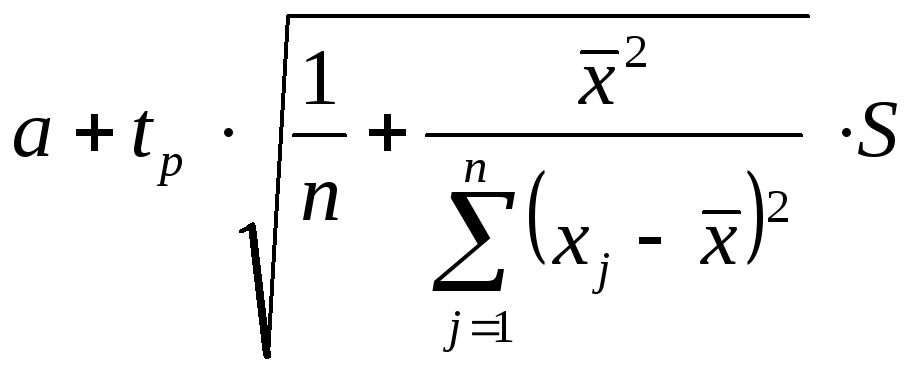 ;
(10.15)
;
(10.15)
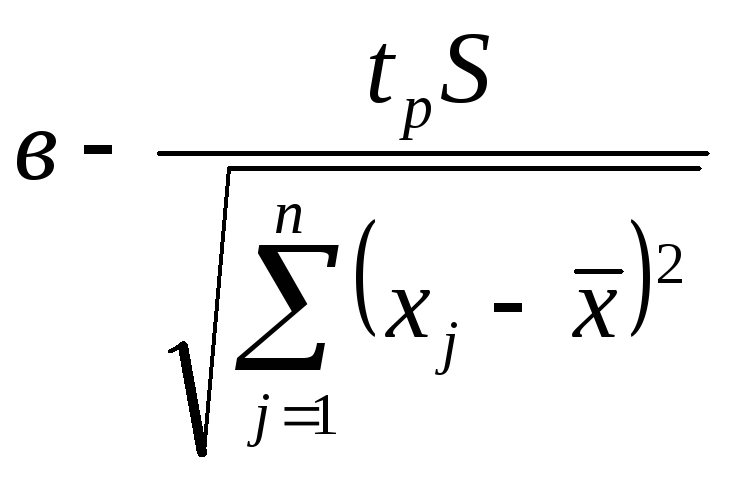 <
В <
<
В <
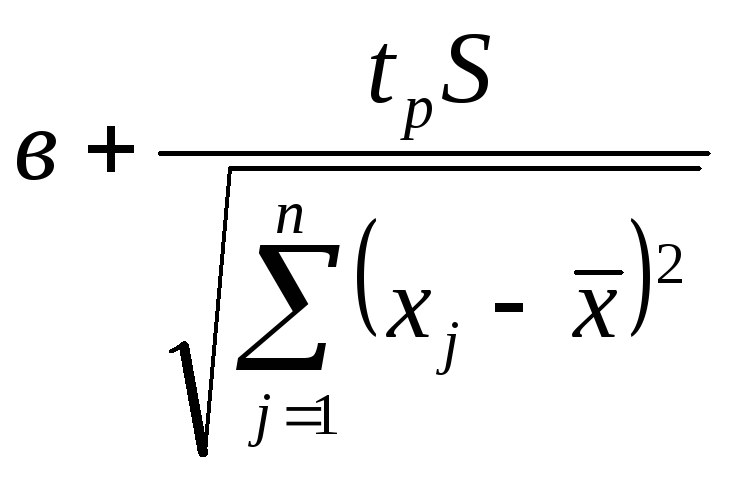 (10.16)
(10.16)
где tp – коэффициент Стьюдента для доверительной вероятности Р и числа степеней свободы f = n-2.
Доверительный интервал для дисперсии линейной модели:
![]() <
<
![]() <
<
![]() , (10.17)
, (10.17)
где 2Н – табличное значение для числа степеней свободы f = n-2 и уровня
значимости
![]() ;
;
2В
– табличное значение 2
для f
= n-2
и
![]() ,
,
где Р – доверительная вероятность.
Доверительный интервал для линии регрессии при каждом значении х0 имеет вид:
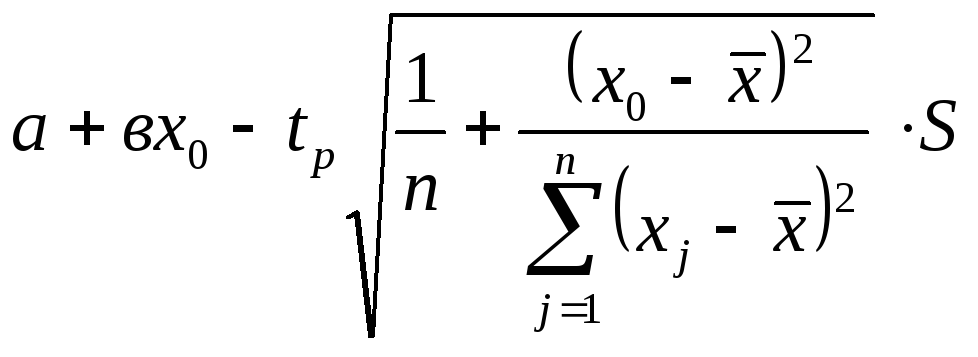 <
A+Bx0<
<
A+Bx0<
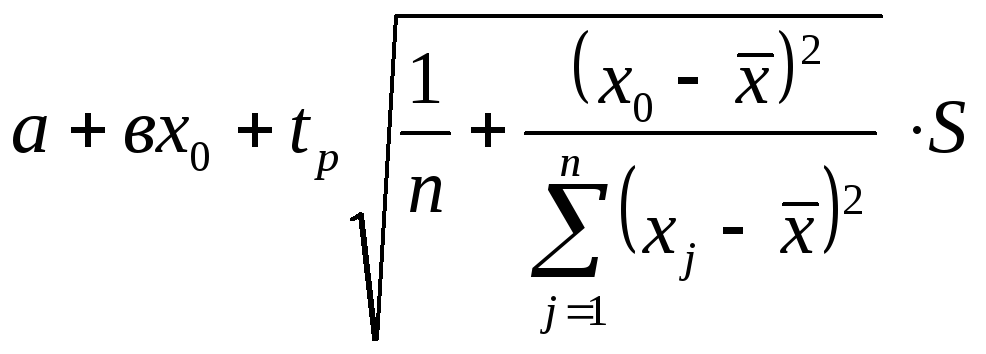 (10.18)
(10.18)
где tp – коэффициент Стьюдента для доверительной вероятности Р и числа степеней свободы f = n-2.
10.1.2.2 Множественная линейная регрессия
Во многих практических задачах однофакторная линейная регрессия даёт недостаточную информацию о зависимой переменной. Большинство процессов зависят от нескольких факторов. Часто даже в случае одного фактора линейное уравнение может оказаться неадекватным. Тогда переходят к множественной линейной регрессионной модели:
![]() У
= а + в1х1
+ в2х2
+…+ вкхк
(10.19)
У
= а + в1х1
+ в2х2
+…+ вкхк
(10.19)
При этом необязательно, чтобы все хi были исходными наблюдаемыми величинами. Например, х1 и х2 могут наблюдаться, х3=х12, х4=log x2, x5=x1x2 и т.д.
При использовании МНК считаем, что все хi являются фиксированными, для любого сочетания хi значения УJ распределены по нормальному закону с постоянным СКО.
Величины вi называются частными коэффициентами регрессии.
Для получения оценок коэффициентов (а, вi) уравнение регрессии МНК нужно минимизировать по а, в1, …вк выражение:
![]() (10.20)
(10.20)
Методика приведения начальных уравнений к системе нормальных уравнений, а также один из способов решения системы рассмотрим в разделе 8.
