Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору

Пусть в трехмерном пространстве задана прямоугольная декартова система координат. Сформулируем следующую задачу:

Составить уравнение плоскости, проходящей через данную точку M(x0,  y0,  z0) перпендикулярно данному вектору  n = {A, B, C} .

Решение. Пусть P(x, y, z) — произвольная точка пространства. Точка P принадлежит плоскости тогда и только тогда, когда вектор MP = {x − x0, y − y0, z − z0} ортогонален вектору n = {A, B, C} (рис.1).

Написав условие ортогональности этих векторов (n, MP) = 0 в координатной форме, получим:

A(x − x0) + B(y − y0) + C(z − z0) = 0

 Уравнение плоскости по трем точкам 

     В векторном виде

     В координатах

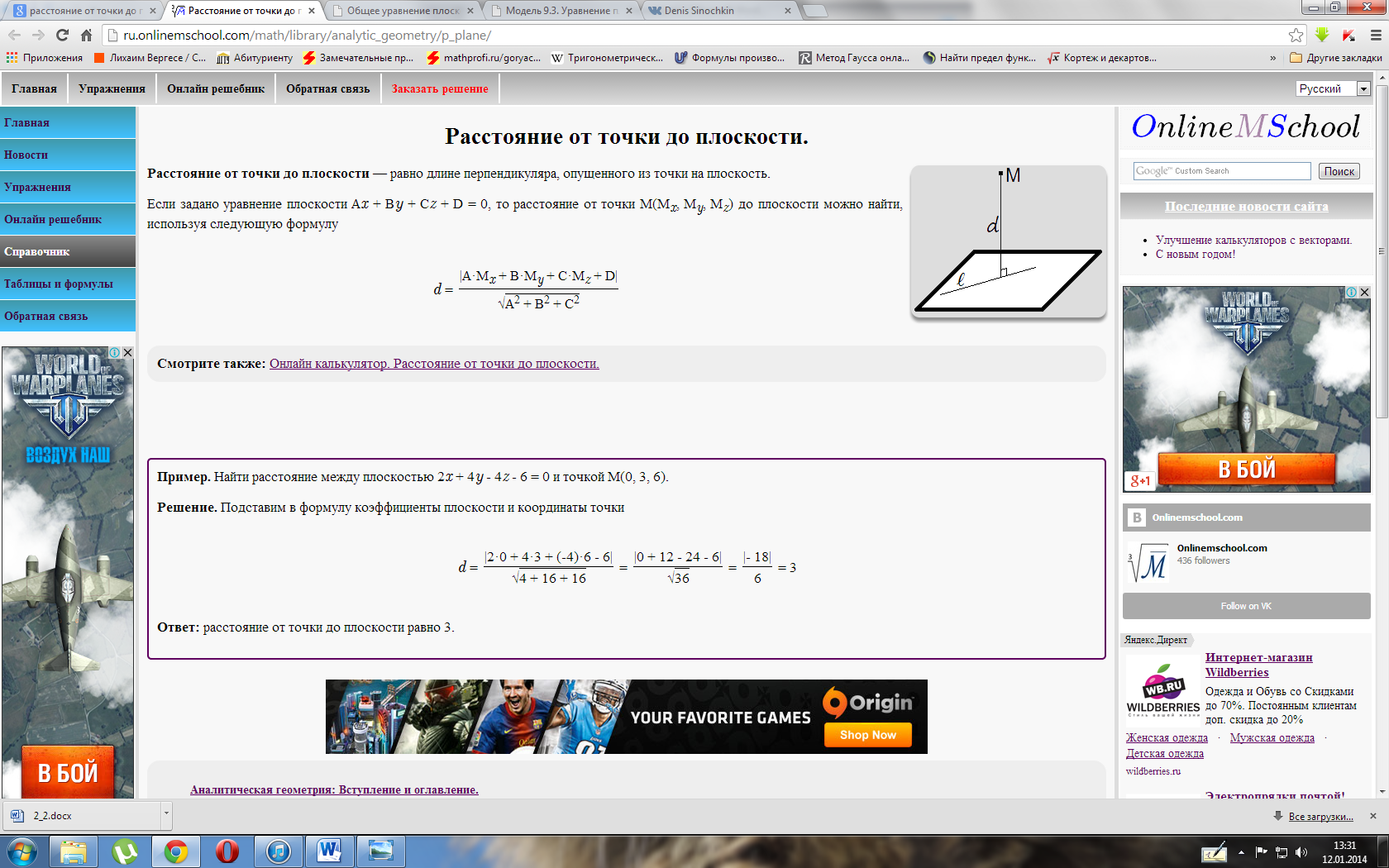
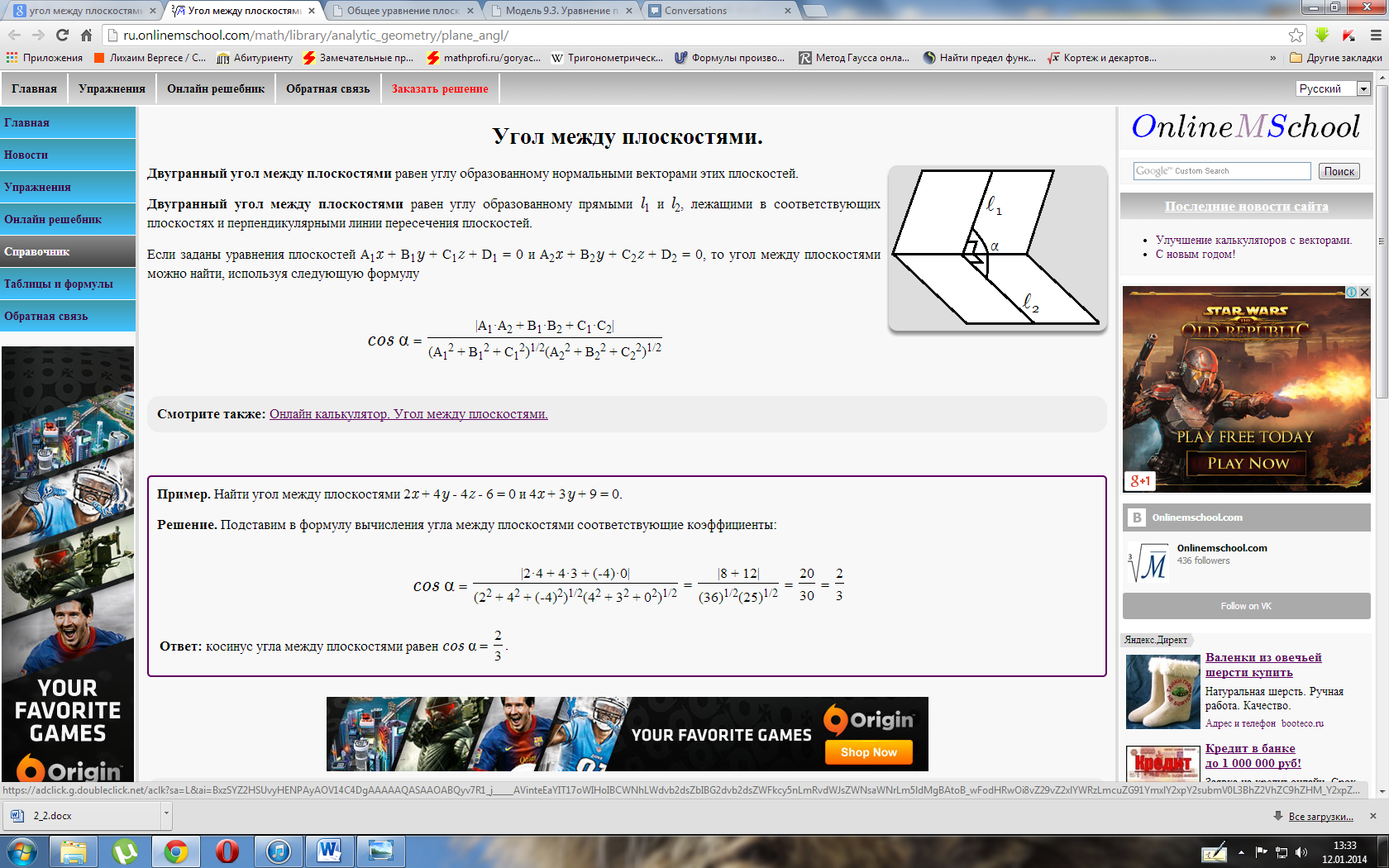
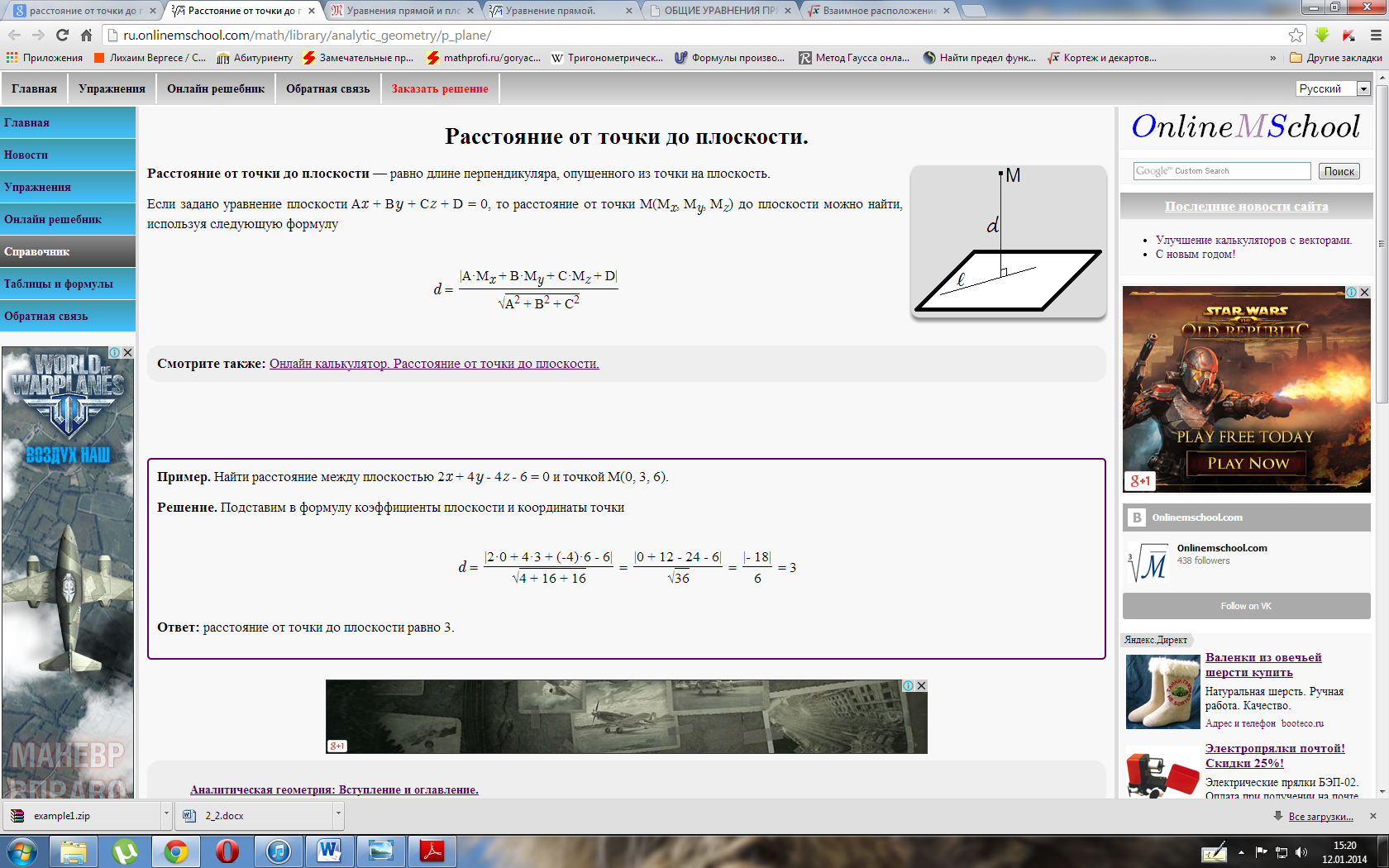
Взаимное расположение плоскостей в пространстве

Пусть

 и 

– общие уравнения двух плоскостей. Тогда:

1) если , то плоскости совпадают;

2) если , то плоскости параллельны;

3)  если  или , то плоскости пересекаются и системауравнений

                         (6)

является уравнениями прямой пересечения данных плоскостей.

3.3

Составить канонические уравнения прямой по точке  и направляющему вектору  Решение: Канонические уравнения прямой составим по формуле: Ответ:

В ряде задач требуется найти какую-нибудь другую точку , принадлежащую данной прямой. Как это сделать? Берём полученные уравнения  и мысленно «отщипываем», например, левый кусочек: . Теперь этот кусочек приравниваем к любому числу (помним, что ноль уже был), например, к единице: . Так как , то и два других «куска» тоже должны быть равны единице. По сути, нужно решить систему:

Составить параметрические уравнения следующих прямых:

Решение: Прямые заданы каноническими уравнениями и на первом этапе следует найти какую-нибудь точку, принадлежащую прямой, и её направляющий вектор.

а) Из уравнений  снимаем точку и направляющий вектор: . Точку можно выбрать и другую (как это сделать – рассказано выше), но лучше взять самую очевидную. Кстати, во избежание ошибок, всегда подставляйте её координаты в уравнения.

Составим параметрические уравнения данной прямой:

Удобство параметрических уравнений состоит в том, что с их помощью очень легко находить другие точки прямой. Например, найдём точку , координаты которой, скажем, соответствуют значению параметра :

Таким образом:  б) Рассмотрим канонические уравнения . Выбор точки здесь несложен, но коварен:  (будьте внимательны, не перепутайте координаты!!!). Как вытащить направляющий вектор? Можно порассуждать, чему параллельна данная прямая, а можно использовать простой формальный приём: в пропорции находятся «игрек» и «зет», поэтому запишем направляющий вектор , а на оставшееся место поставим ноль: .

Составим параметрические уравнения прямой:

в) Перепишем уравнения  в виде , то есть «зет» может быть любым. А если любым, то пусть, например, . Таким образом, точка  принадлежит данной прямой. Для нахождения направляющего вектора используем следующий формальный приём: в исходных уравнениях  находятся «икс» и «игрек», и в направляющем векторе на данных местах записываем нули: . На оставшееся место ставим единицу: . Вместо единицы подойдёт любое число, кроме нуля.

Запишем параметрические уравнения прямой: