Геометрическая интерпретация скалярного произведения.
Скалярное произведение (a, b) векторов a и b равно произведению модулей этих векторов на косинус угла между этими векторами.
То есть (a, b) =|a| · |b| cos∠(a, b),
где ∠(a, b) есть угол между векторами a и b :
Проекцией
вектора b на
вектор a, 
,
будем называть проекцию вектора b на
любую ось, параллельную вектору a и
имеющую направление, совпадающее с
направлением вектора a.
2,4
2,5
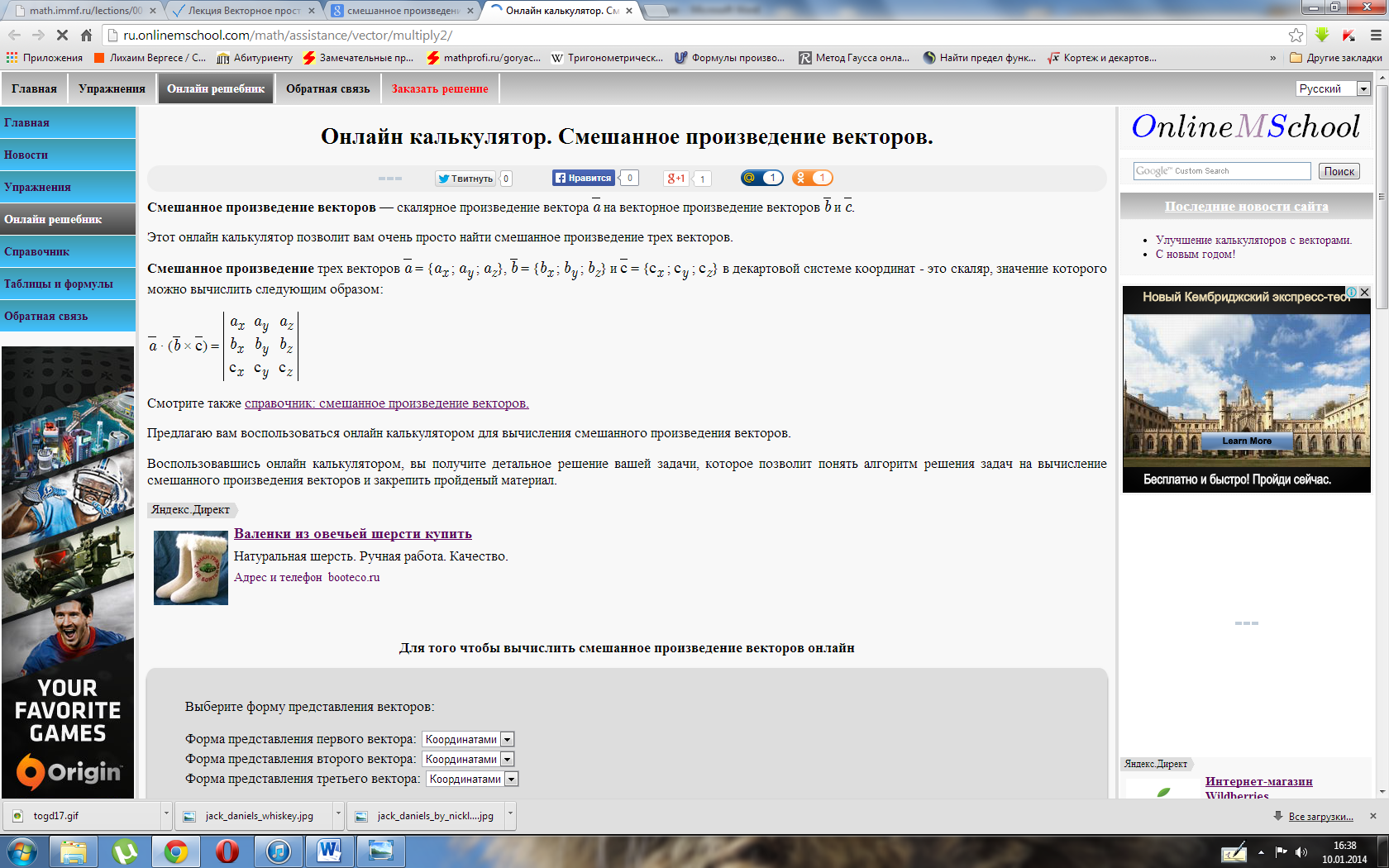
Сме́шанное
произведе́ние 
векторов 
— скалярное
произведение вектора 
на векторное
произведение векторов 
и 
:
.
Геометрический
смысл смешанного произведения: если тройка
векторов 
правая,
то их смешанное произведение равно
объему параллелепипеда построенного
на этих векторах: 
.
В случае левой тройки 
смешанное
произведение указанных векторов равно
объему параллелепипеда со знаком
минус: 
.
Если 
, 
и 
компланарны,
то их смешанное произведение равно
нулю.
Итак,
из выше сказанного можно сделать вывод,
что объем параллелепипеда, построенного
на векторах 
, 
и 
равен
модулю смешанного произведения этих
векторов:
Объем пирамиды, построенной на этой тройке векторов равен
Свойства смешанного произведения:
1° 
2° 
3°
Три вектора
компланарны тогда
и только тогда, когда 
4°
Тройка векторов является правой тогда
и только тогда, когда 
.
Если же 
,
то векторы 
, 
и 
образуют
левую тройку векторов.
5° 
6° 
7° 
8° 
9° 
10°
Тождество Якоби: 
Если
векторы 
, 
и 
заданы
своими координатами, то их смешанное
произведение вычисляется по формуле
Теорема 4.10. Векторное произведение линейно по каждому из сомножителей. Доказательство. В силу теоремы 4.6 достаточно показать, что для любых векторов a, b, c и любого числа α ∈ R имеют место равенства [a +b, c] = [a, c] + [b, c] и [αa, b] = α[a, b]. Пусть d = [a +b, c] - [a, c] - [b, c]. Тогда (d, d) = (a + b, c, d) - (a, c, d) - (b, c, d). Из линейности смешанного произведения следует, что (d, d) = (a, c, d) + (b, c, d)- (a, c, d) - (b, c, d) = 0. Это доказывает первое из требуемых равенств. Второе равенство доказывается аналогично. Теорема доказана.
Теорема 4.6. Векторное произведение антикоммутативно, т.е. [a, b] = -[b, a], ∀ a, b. Доказательство.Утверждение теоремы очевидно, если a и b коллиниарны. Пусть a и b не коллиниарны, тогда [a, b] ≠ 0, [b, a] ≠ 0, при этом |[a, b]| = |[b, a]| = Sab и [a, b], [b, a] перпендикулярны плоскости π (a, b). Значит, либо [a, b] = [b, a], либо [a, b] = - [b, a]. Но вектор [b, a] ≠ [a, b], так как тройка векторов b, a, [b, a] − правая (по определению векторного произведения) и, следовательно, тройка a, b, [b, a] − левая. Теорема доказана.
Смешанное произведение линейно по каждому аргументу.
Линейность операции по какому-то аргументу означает выполнение двух условий:
1) если аргумент умножить на число, то и результат умножится на это число, то есть числовой множитель аргумента можно вынести за знак операции;
2) если аргумент заменить суммой двух слагаемых, то результат будет равен сумме результатов для каждого слагаемого.
В частности, утверждение, что смешанное произведение линейно по второму аргументу, означает:
1) 
;
2) 
.
Доказательство предложения
10.28.
Соотношения 
и 
следуют
из того, что abc является
скалярным произведением a на 
и
из линейности скалярного произведения
(свойства 2,3, теорема
10.2).
Для
второго аргумента: в силу равенства (10.8)
выполнено 
,
поэтому
Для третьего аргумента свойство линейности доказывается аналогично.
3,1
