Текст задания:

1. Данные  комплексные  числа  изобразить  точками плоскости:

а)   1 + i;           в) —2 + 3i;         д) 5+ 0i;            ж) 0 + 5i

б)  1 — i;           г) —3 — 2i;         е) —6 + 0i;         з) 0 — 4i.

2.   Какие комплексные числа изображают   на рисунке 330 точки А, В, C,D и О?

3.  Дать   геометрическую интерпретацию формулам:

а)  (1 +2i) + (l — 2i)=2 + 0i;

б)  (3 — 4i)+(— 1 + 2i) = 2—2i.

4.  Пусть точка М служит изображением на плоскости комплексного числа а + bi.

 Построить на той же плоскости точки, которые изображали бы комплексные числа:

a) а — bi;           д) 0 + bi

б)  — а + bi;      е) — а + 0i;

в)  — а — bi     ж) 0 — bi.

г)  а + 0i;

5. Пусть точка М служит изображением на плоскости комплексного числа а — bi. Где на той же плоскости расположены точки, изображающие числа:

а)  3а + 0i ;         г) 0 + 2bi

б)  — 5а + 0i;    д) 4а + 3bi .

в) 0 — bi;

Раздел 2. Корни, степени, логарифмы. Функции, их свойства и графики.

Уравнения и неравенства

Самостоятельная работа № 3

Тема: Преобразование иррациональных выражений.

Цель: закрепить знания и умения студентов по освоению применения формул при выполнении вычислений и решении иррациональных уравнений.

Теоритическое обоснование:

     Корень n-й степени     - арифметический кореньn-й степени из числа 

 Свойства:

  В частности, - арифметический квадратный корень:     Степень с дробным (рациональным) показателем 

Пример 1

 . Пример 2 . Пример 3 Освободиться от иррациональности в знаменателе дроби: .

Текст задания:

Упростить иррациональные выражения:

1. 

2. 

3. 4.;

5. ; 

6. .

Самостоятельная работа № 4

Тема: Степени с действительным показателем, действия со степенями.

Цель: закрепить знания и умения студентов по освоению свойств показательной функции.

Теоритическое обоснование:

 Свойства степени с действительным показателем 

Пример 1. Вычислить: . Решение.  ; ;  . Отсюда: .  Пример 2. Выполнить действия: . Решение.  ; . Отсюда: 5³∙2⁴+5=(5∙2)³∙2+5=2000+5=2005. Пример 3. .

Текст задания:

1. Расположить в порядке возрастания следующие числа: 

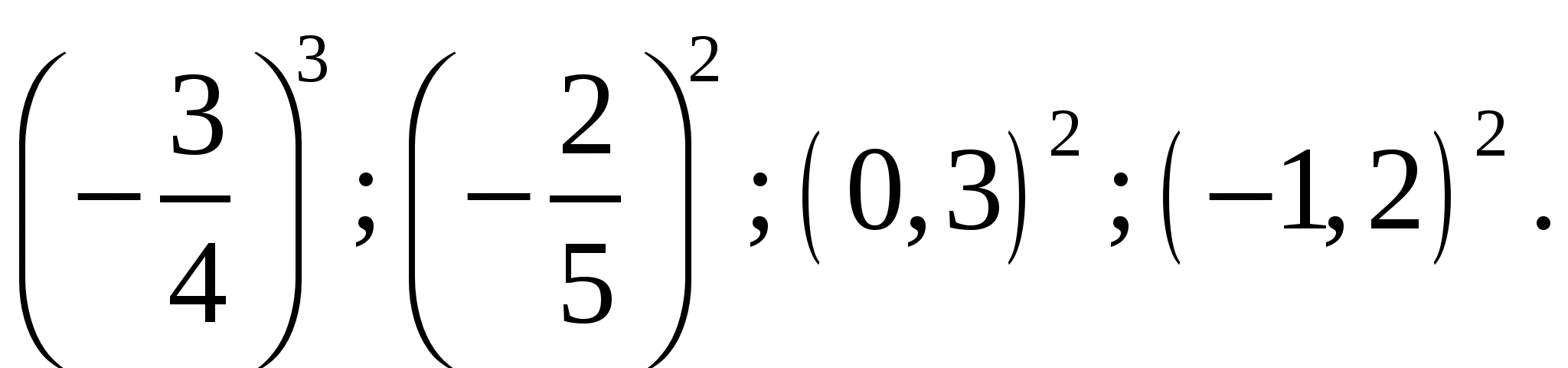
2.  Вычислить: .

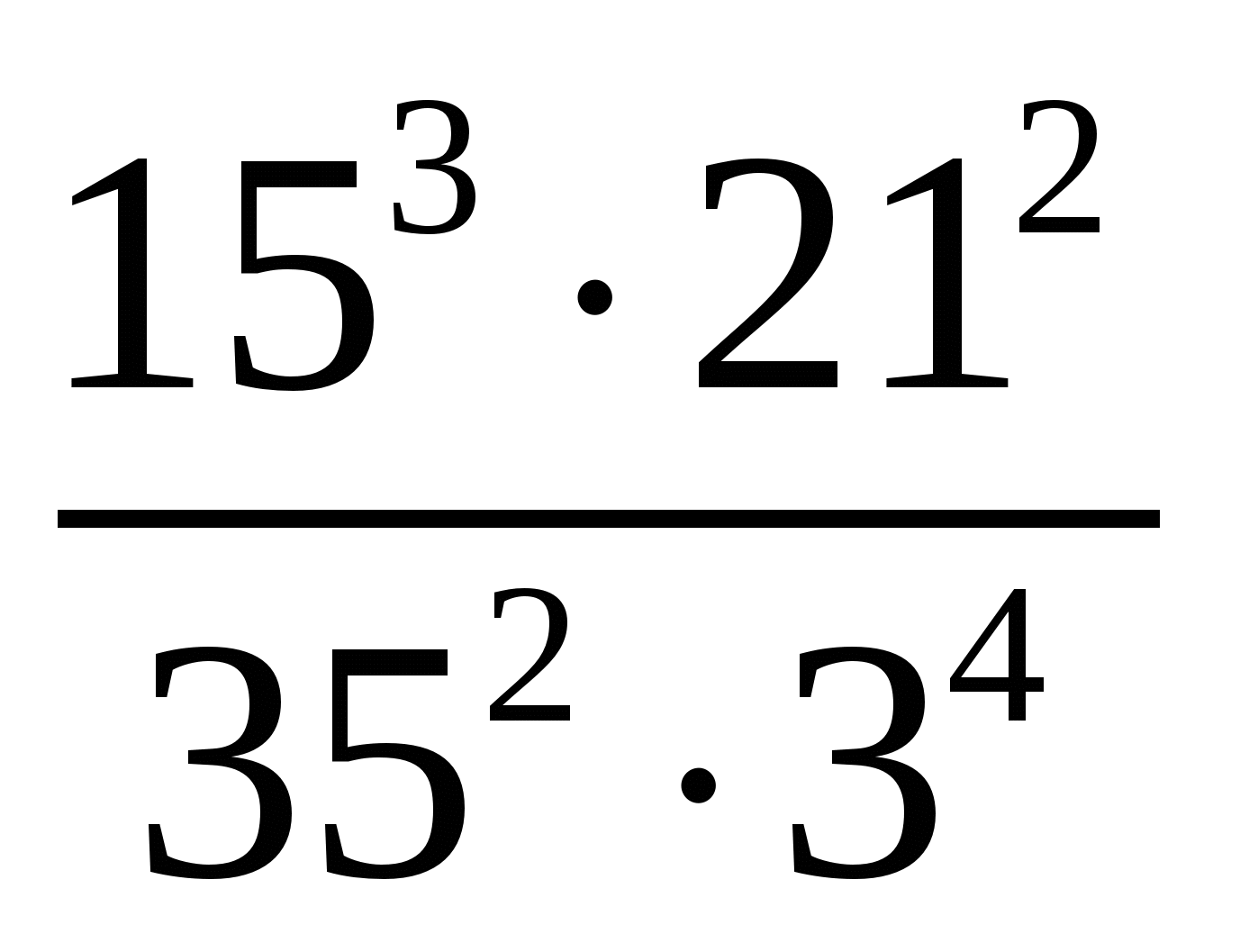3. Упростить: .

4. Найти значение выражения: .

5.  Вычислить: ;

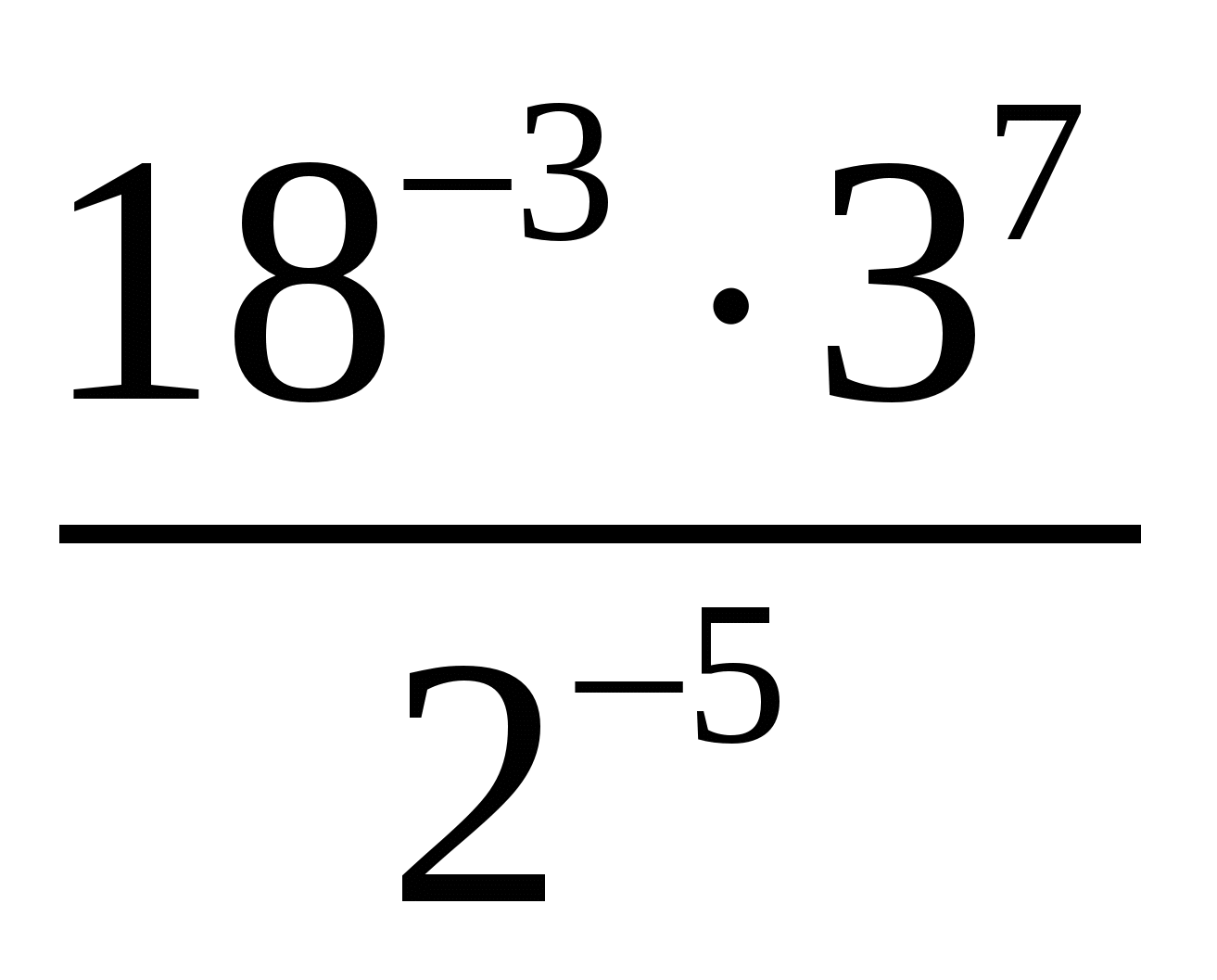6. Вычислить:  а) 3,2⁰ + 64^1/6 – 0,2³ ·0,2^-2 – 5³ : 5; б) 27^1/3 – 4,8⁰ – 1,5³ –1,5^-2 + 2² : 2^-3; 

в) 5² : 5^-1 + - 4² · 4^-3 – 27^2/3.

Самостоятельная работа № 5

Тема: Правило перехода логарифма к новому основанию.

Цель: закрепить знания и умения студентов по освоению логарифмов и свойств логарифмической функции.

Теоритическое обоснование:

Формулы и свойства логарифмов

Логарифмомчислапо основанию() называется такое число, что, то есть записииравносильны. Логарифм имеет смысл, если.

Если немного перефразировать - Логарифмчислапо основаниюопределяется как показатель степени, в которую надо возвести число, чтобы получить число(Логарифм существует только у положительных чисел).

Логарифм в переводе с греческого буквально означает "число, изменяющее отношение".

Специальные обозначения:

1. Натуральный логарифм - логарифм по основанию , где - число Эйлера.

2. Десятичный логарифм - логарифм по основанию 10.

Свойства логарифмов:

1°    -основное логарифмическое тождество.

2°    

3°    

Логарифм единицы по любому положительному, отличному от 1, основанию равен нулю. Это возможно потому, что из любого действительного числа можно получить 1 только возведя его в нулевую степень.

4°    -логарифм произведения.

Логарифм произведения равен сумме логарифмов сомножителей.

5°    -логарифм частного.

Логарифм частного (дроби) равен разности логарифмов сомножителей.

6°    -логарифм степени.

Логарифм степени равен произведению показателя степени на логарифм ее основания.

7°    

8°    

9°    - переход к новому основанию.