3.2. Определение сил и моментов сил инерции

В динамических расчетах главный вектор сил инерции и главный момент в случае сложного движения звена определяется по формулам

; ( 3.1 )

М, ( 3.2)

где m – масса звена; - вектор ускорения центра масс;J_s – момент инерции звена относительно оси, проходящей через центр масс, перпендикулярно плоскости движения; ε – угловое ускорение звена.

Для вычисления сил инерции надо определить ускорения а_s и ε или из плана скоростей, или аналитически.

В частных случаях движения звеньев (поступательное или вращательное) остается или только главный вектор сил инерции, или главный момент сил. Аналитически силы инерции в плоском движении определяются как: = –m; = -m; М_ин = – J_s ε .

3.3. Величина и направление реакций

В плоских механизмах звенья могут образовывать низшие (вращательные и поступательные пары) и высшие кинематические пары, у которых касание элементов происходит либо в точке, либо по линии. Во вращательной паре без учета силы трения (рис.3.2,а) давление на цилиндрическую поверхность распределено по определенному закону, зависящему от степени приработанности поверхностей, смазки и т. д. Если силами трения пренебречь, то равнодействующая их проходит через центр шарнира О. Величина и направление силы неизвестны и должны быть определены из кинематического расчета. В идеальной поступательной паре (рис.3.2,б) реакциянормальна к направляющим, но величина и точка приложения её неизвестны. Таким образом, в низших парах при наличии плоской системы сил, действующих на звенья механизма, необходимо иметь два уравнения, что совпадает с числом условий связи, накладываемых кинематической парой плоского механизма.

В высшей кинематической паре (рис.3.2,в) реакция нормальна к поверхности. Определению подлежит только её величина. И здесь число уравнений, которые нужно составить для определения реакций, совпадает с числом условий связи, накладываемых кинематической парой.

Если число звеньев в группе – n , то для них можно составить 3n уравнений равновесия. При соединении звеньев только кинематическими парами 5 класса число неизвестных реакций будет равно 2р₅. Каждую силу можно определить в том случае, если число уравнений равновесия равно числу неизвестных компонентов сил, т.е. условием статической определимости групп звеньев при действии на них плоской системы сил является равенство

3n – 2р₅ =0.

Это условие совпадает с условием, которому удовлетворяют группы звеньев, именуемые группами Ассура.

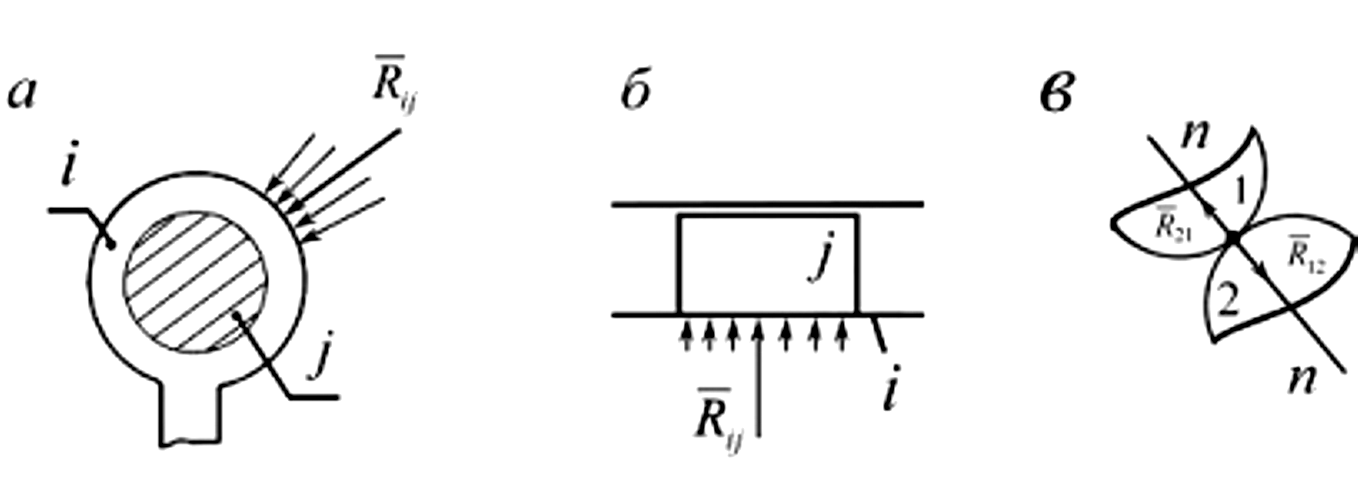
Рис.3.2. Реакции в кинематических парах

3.4. Пример определения реакций в механизме

Рассмотрим пример определения реакций в кинематических парах кривошипно-ползунного механизма (рис.3.3). Предварительно строим планы скоростей и ускорений в соответствующих масштабах. Выделим в механизме двухповодковую группу Ассура ( звенья 2-3) и начальное звено 1. К группе Ассура приложим последовательно все внешние силы, силы и моменты сил инерции и реакции со стороны отброшенных звеньев и реакции в связанных кинематических парах. Внешние силы: силы тяжести иприкладываем в центрах масс (точкиs₂ и s₃), силу технологического сопротивления прикладываем к ведомому звену 3 (ползуну). Силы и моменты сил инерции вычисляются по формулам (3.1) и (3.2).

Составим сумму моментов сил, действующих на 2-е звено (рис.3.4,а): ,

откуда находим величину реакции . Направление её мы задали (рис.3.4,а). Если при расчетеполучаем со знаком ( – ), то это направление учитывается, когда решается векторное уравнение (. Плечи силh измеряются с чертежа в мм и умножаются на масштабный коэффициент ,- длина звена в м.

Запишем векторные уравнения сил, действующих на 2-е и 3-е звенья, а затем их суммируем. Имеем

,

,

.

(

В последнем уравнении содержится две неизвестные: величины и, которые можно определить, решая последнее векторное уравнение графически. Для этого строится план сил (рис.3.4,б).

Уравновешивающую силу, приложенную к зубчатому колесу, жестко связанному с начальным звеном, (рис.3.5,а) найдем, рассматривая его равновесие. Приложим все силы: реакцию в точкеА, реакцию в точке О₁ и уравновешивающую силу в полюсеР зацепления зубчатых колес 1 и 2, направленную по линии зацепления N – N. Плечо действия этой силы относительно т.О₁ равно радиусу основной окружности 1-го колеса r_в = r₁·cosα=(mz₁/2)·cos20º.

Составим сумму моментов сил, действующих на начальное звено относительно точки О₁ .

Отсюда находим . Запишем векторную сумму сил для первого звена0 (рис.3.5,б) и из векторного многоугольника определяем реакцию.

К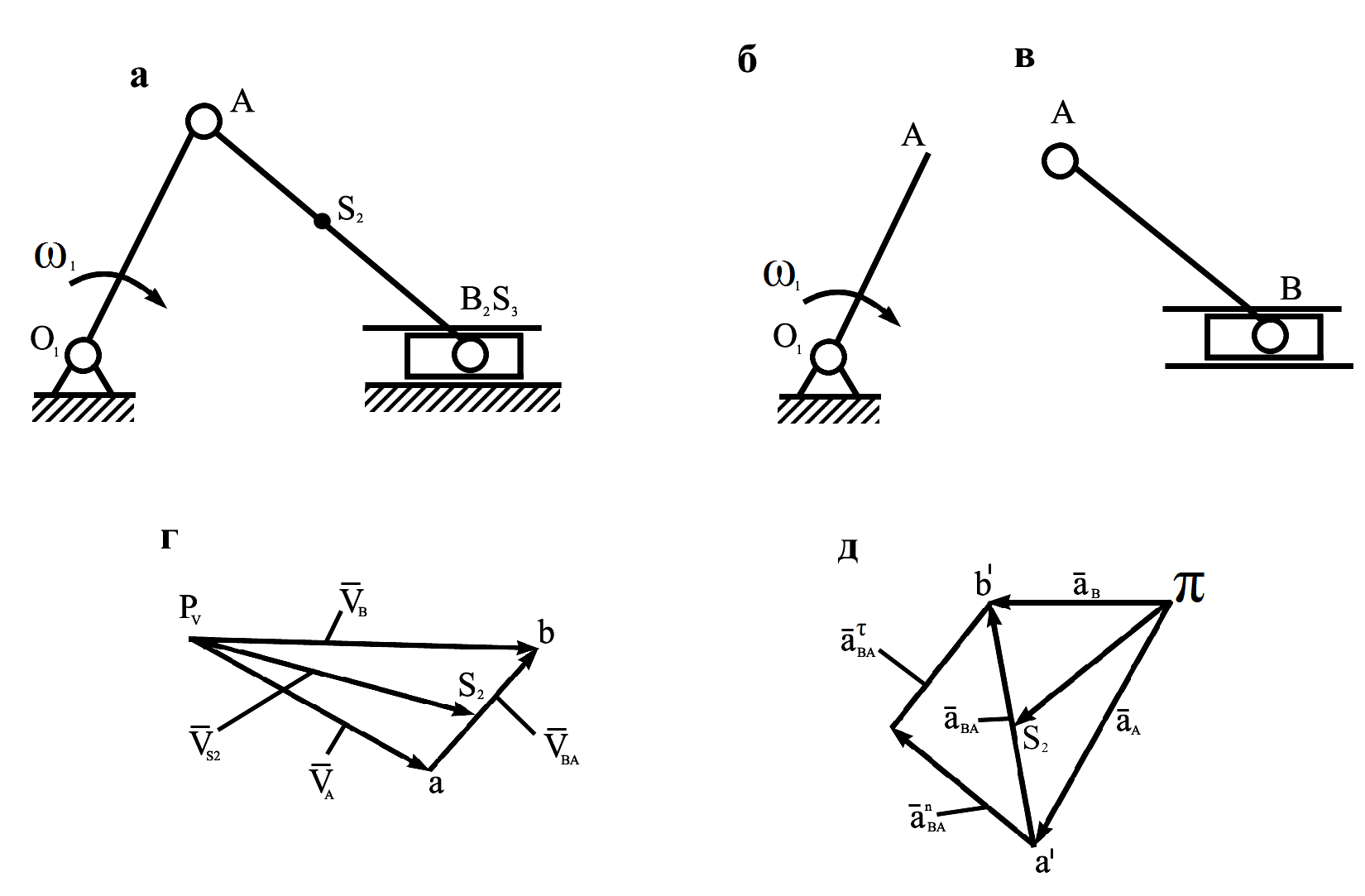огда начальное звено приводится в движение от привода через муфту, то уравновешивающий моментМ_ур (рис.3.6, а) равен М_ур= , а реакция в опоренаходится из решения векторного уравнения (рис.3.6,б)=0.

Рис.3.3. Кривошипно-ползунный механизм а – схема механизма, б – начальное звено, в – группа Ассура, г – план скоростей, д – план ускорений

Рис.3.4. Кинетостатика группы Ассура

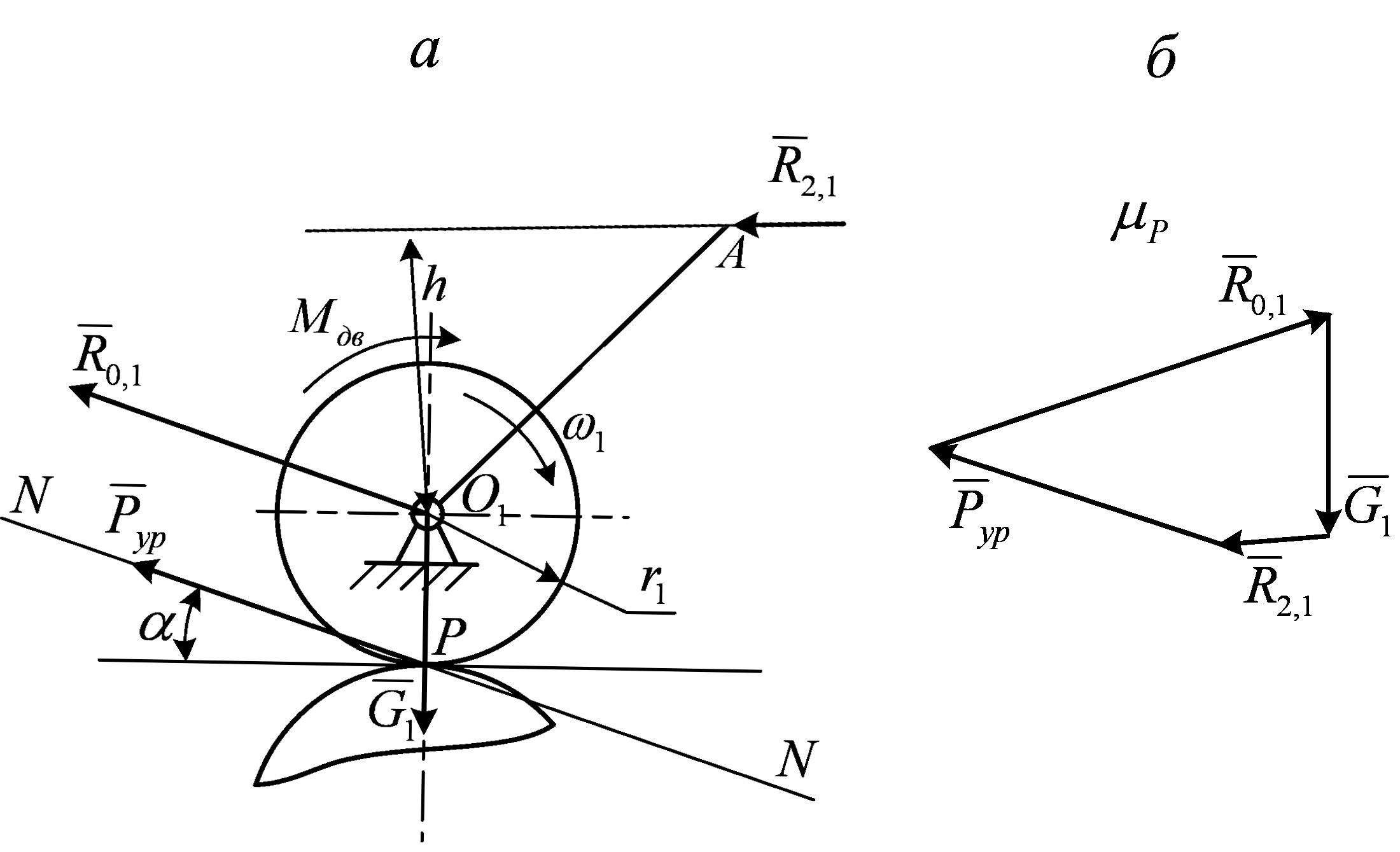
Рис.3.5. К определению уравновешивающей силы

Рис.3.6. К определению уравновешивающего момента