
Переходные процессы и косвенные оценки.
№1
Что определяют с помощью построенного процесса регулирования (убрать неправильный ответ):
1. Время регулирования
2. Колебательность
![]() системы.
системы.
3. Вид процесса (апериодический, колебательный).
4. Перерегулирование.
№2
Дифференциальное уравнение системы
имеет вид:
![]() .
При каком входном сигнале в момент
.
При каком входном сигнале в момент![]() координата и ее производная
координата и ее производная![]() не будут иметь разрывы первого рода:
не будут иметь разрывы первого рода:
1.
![]() 3.
3.![]()
2.
![]() 4.
4.![]() .
.
№3
В момент времени
![]() левые и правые начальные условия по
управляемой переменной и ее производным
не совпадают. Возможно ли в этом случае
аналитическое решение дифференциального
уравнения САУ и, если да, то как:
левые и правые начальные условия по
управляемой переменной и ее производным
не совпадают. Возможно ли в этом случае
аналитическое решение дифференциального
уравнения САУ и, если да, то как:
1. Решение невозможно.
2. Да, при этом в изображениях по Лапласу
производных функций
![]() должны учитываться левые начальные
условия.
должны учитываться левые начальные
условия.
3. Да, при этом в изображениях по Лапласу
производных функций
![]() должны учитываться левые начальные
условия по
должны учитываться левые начальные
условия по![]() и правые по
и правые по![]() .
.
4. Да, при этом в изображениях по Лапласу
производных функций
![]() должны учитываться правые начальные
условия по
должны учитываться правые начальные
условия по![]() и левые по
и левые по![]() .
.
№4
Дифференциальное уравнение системы
имеет вид:
![]() .
При каком входном сигнале в момент
.
При каком входном сигнале в момент![]() координата или ее производная
координата или ее производная![]() будут иметь разрывы первого рода:
будут иметь разрывы первого рода:
1.
![]() 3.
3.![]()
2.
![]() 4.
4.![]() .
.
№5
При частотном методе построения
переходного процесса управляемая
переменная определяется зависимостью
![]() .
В числителе подынтегрального выражения
на пустом месте находится:
.
В числителе подынтегрального выражения
на пустом месте находится:
1. Вещественная частотная характеристика замкнутой системы.
2. Вещественная частотная характеристика разомкнутой системы.
3. Мнимая частотная характеристика замкнутой системы.
4. Мнимая частотная характеристика разомкнутой системы.
№6
При частотном методе построения
переходного процесса управляемая
переменная определяется зависимостью
![]() .
В числителе подынтегрального выражения
на пустом месте находится:
.
В числителе подынтегрального выражения
на пустом месте находится:
1. Вещественная частотная характеристика замкнутой системы.
2. Вещественная частотная характеристика разомкнутой системы.
3. Мнимая частотная характеристика замкнутой системы.
4. Мнимая частотная характеристика разомкнутой системы.
№7
Дифференциальное уравнение САУ имеет
вид
![]() .
Входной сигнал
.
Входной сигнал![]() .
В какие моменты времени возникают скачки
по управляемой переменной
.
В какие моменты времени возникают скачки
по управляемой переменной![]() или
ее производной:
или
ее производной:
1. При
![]() 3.
При
3.
При![]()
2. При
![]() и
и![]() 4.
При
4.
При![]() .
.
№8
Дифференциальное уравнение САУ имеет
вид
![]() .
Входной сигнал
.
Входной сигнал![]() .
В некоторые моменты времени возникают
скачки по управляемой переменной
.
В некоторые моменты времени возникают
скачки по управляемой переменной![]() или ее производной. Для выполнения
численного расчета переходного процесса
данное уравнение должно быть приведено
к виду:
или ее производной. Для выполнения
численного расчета переходного процесса
данное уравнение должно быть приведено
к виду:
1.
![]() 3.
3.![]()
2.
![]() 4.
4.
![]() .
.
№9
Дифференциальное уравнение САУ имеет
вид
![]() .
Входной сигнал
.
Входной сигнал![]() .
В некоторые моменты времени возникают
скачки по управляемой переменной
.
В некоторые моменты времени возникают
скачки по управляемой переменной![]() или ее производной. Для выполнения
численного расчета переходного процесса
данное уравнение должно быть приведено
к виду:
или ее производной. Для выполнения
численного расчета переходного процесса
данное уравнение должно быть приведено
к виду:
1.
![]() 3.
3.![]()
2.
![]() 4.
4.![]() .
.
№10
АФЧХ замкнутой системы
![]() .
Установившееся значение переходной
характеристики
.
Установившееся значение переходной
характеристики![]() равно:
равно:
1.
![]() 3.
3.![]()
2.
![]() 4.
4.![]() .
.
№11
АФЧХ замкнутой системы
![]() .
Достаточным условием того, что
перерегулирование%
не превышает 18%, является выполнение
условия:
.
Достаточным условием того, что
перерегулирование%
не превышает 18%, является выполнение
условия:
1.
![]() может быть представлена как разность
3 положительных не возрастающих функций
частоты.
может быть представлена как разность
3 положительных не возрастающих функций
частоты.
2.
![]() -
положительная не возрастающая функция
частоты.
-
положительная не возрастающая функция
частоты.
3.
![]() - положительная не возрастающая функция
частоты.
- положительная не возрастающая функция
частоты.
4.
![]() может быть представлена как разность
2 положительных не возрастающих функций
частоты.
может быть представлена как разность
2 положительных не возрастающих функций
частоты.
№12
Если ВЧХ замкнутой САУ является положительной не возрастающей функцией частоты, то:
1. Переходная характеристика
![]() является монотонно возрастающей
функцией.
является монотонно возрастающей
функцией.
2. Импульсная переходная функция
![]() является монотонно возрастающей
функцией.
является монотонно возрастающей
функцией.
3. В переходном процессе перерегулирование не превышает 18%.
4. Процесс регулирования будет заведомо немонотонной функцией времени.
№13
Для того, чтобы переходный процесс был монотонным достаточно, чтобы:
1. Вещественная частотная характеристика
![]() являлась положительной не возрастающей
функцией.
являлась положительной не возрастающей
функцией.
2. Производная
![]() была отрицательной, убывающей по модулю
функцией и
была отрицательной, убывающей по модулю
функцией и![]() .
.
3. Производная
![]() была положительной, убывающей по модулю
функцией и
была положительной, убывающей по модулю
функцией и![]() .
.
4. Вещественная частотная характеристика
![]() может быть представлена как разность
2 положительных не возрастающих функций
частоты.
может быть представлена как разность
2 положительных не возрастающих функций
частоты.
№14
Если вещественная частотная характеристика
![]() (
(![]() ,
,![]() -
максимальное значение ВЧХ) может быть
представлена как разность 2 положительных
не возрастающих функций частоты, то:
-
максимальное значение ВЧХ) может быть
представлена как разность 2 положительных
не возрастающих функций частоты, то:
1. Переходная характеристика
![]() является монотонно возрастающей
функцией.
является монотонно возрастающей
функцией.
2. В переходном процессе перерегулирование не превышает 18%.
3. Перерегулирование
![]() не превышает
не превышает![]() .
.
4. Процесс регулирования будет заведомо немонотонной функцией времени.
№15
Степень устойчивости
![]() это:
это:
1. Модуль вещественной части корня, ближайшего к вещественной оси.
2. Модуль вещественной части корня, ближайшего к мнимой оси.
3. Модуль мнимой части корня, ближайшего к мнимой оси.
4. Модуль мнимой части корня, ближайшего к вещественной оси.
№16
Характеристическое уравнение системы
имеет следующие корни:
![]() .
Степень устойчивости
.
Степень устойчивости![]() равна:
равна:
1. -2 2. 0,63. 6 4. 1/2.
№17
Характеристическое уравнение системы
имеет следующие корни:
![]() .
Степень устойчивости
.
Степень устойчивости![]() равна:
равна:
1. 12. 2,5 3. 1,2 4. -1.
№18
Пусть
![]() -
величина «коридора», определяющего
окрестность установившегося значения
управляемой величины, по которой
находится время регулирования
-
величина «коридора», определяющего
окрестность установившегося значения
управляемой величины, по которой
находится время регулирования![]() ,
,![]() - степень устойчивости. Приближенная
оценка времени регулирования имеет
вид:
- степень устойчивости. Приближенная
оценка времени регулирования имеет
вид:
1.
![]() 3.
3.
![]()
2.
![]() 4.
4.![]() .
.
№19
Пусть
![]() -
величина «коридора», определяющего
окрестность установившегося значения
управляемой величины, по которой
находится время регулирования
-
величина «коридора», определяющего
окрестность установившегося значения
управляемой величины, по которой
находится время регулирования![]() ,
,![]() - степень устойчивости. При
- степень устойчивости. При![]() приближенная оценка времени регулирования
имеет вид:
приближенная оценка времени регулирования
имеет вид:
1.
![]() 3.
3.![]()
2.
![]() 4.
4.![]() .
.
№20
Номограмма Солодовникова определяет:
1. Зависимость
перерегулирования
![]() и времени регулирования
и времени регулирования![]() от максимального значения ВЧХ
от максимального значения ВЧХ![]() .
.
2. Зависимость установившейся ошибки
от максимального значения ВЧХ
![]() .
.
3. Зависимость избытка по амплитуде и
избытка по фазе от максимального значения
ВЧХ
![]() .
.
4. Зависимость избытка по амплитуде и
избытка по фазе от минимального значения
ВЧХ
![]() .
.
№21
Характеристическое уравнение системы
третьего порядка имеет следующие корни:
![]() .
Колебательность системы
.
Колебательность системы![]() определяется выражением:
определяется выражением:
1.
![]() 3.
3.![]()
2.
![]() 4.
4.![]() .
.
№22
С увеличением колебательности
![]() :
:
1. Колебания в системе затухают сильнее.
2. Затухание колебаний не зависит от этого параметра.
3. Апериодическая составляющая процесса регулирования затухает сильнее.
4. Колебания в системе затухают слабее.
№23
В системе заданы ограничения на степень
устойчивости
![]() ,
так что выполняется условие
,
так что выполняется условие![]() и колебательность
и колебательность![]() ,
так что выполняется условие
,
так что выполняется условие![]() .
При этом область возможного расположения
корней характеристического уравнения
на комплексной плоскости «р» имеет
вид:
.
При этом область возможного расположения
корней характеристического уравнения
на комплексной плоскости «р» имеет
вид:
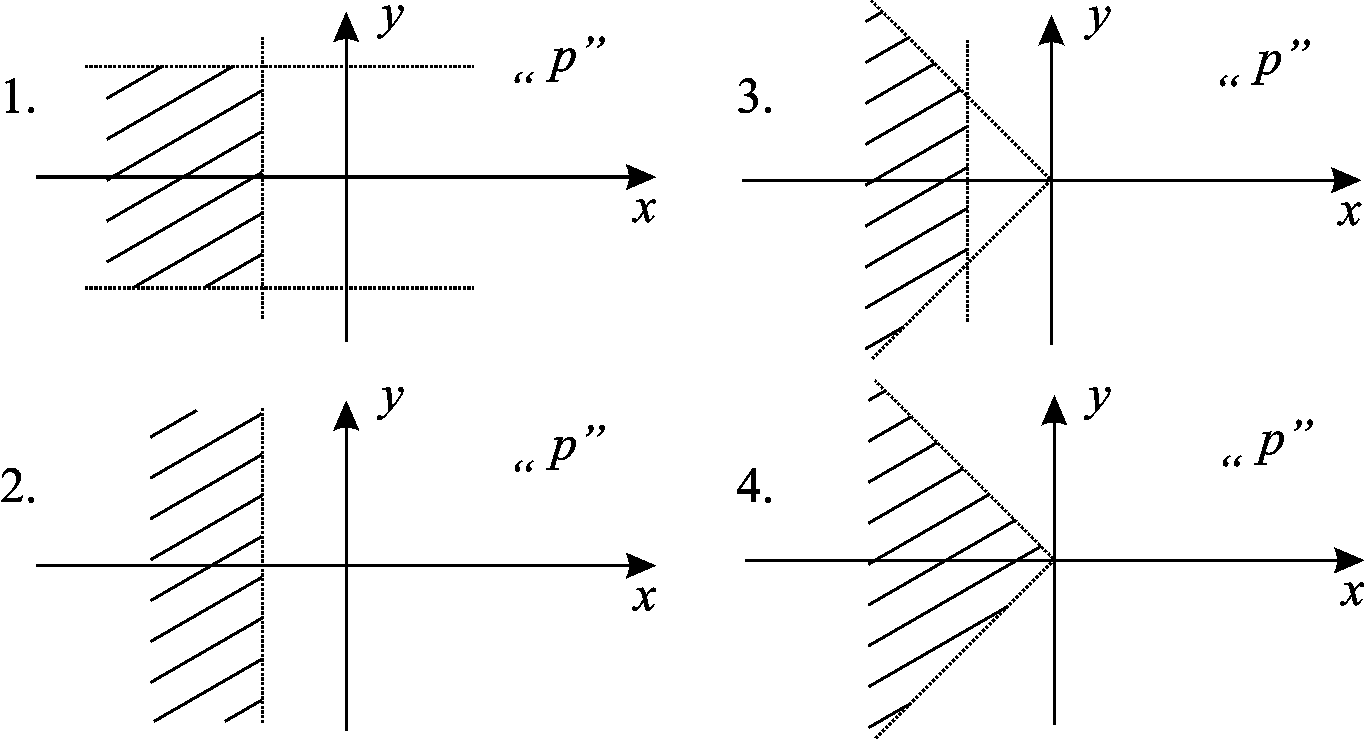 4
4
№24
В системе заданы ограничения на степень
устойчивости
![]() ,
так что выполняется условие
,
так что выполняется условие![]() .
При этом область возможного расположения
корней характеристического уравнения
на комплексной плоскости «р» имеет
вид:
.
При этом область возможного расположения
корней характеристического уравнения
на комплексной плоскости «р» имеет
вид:
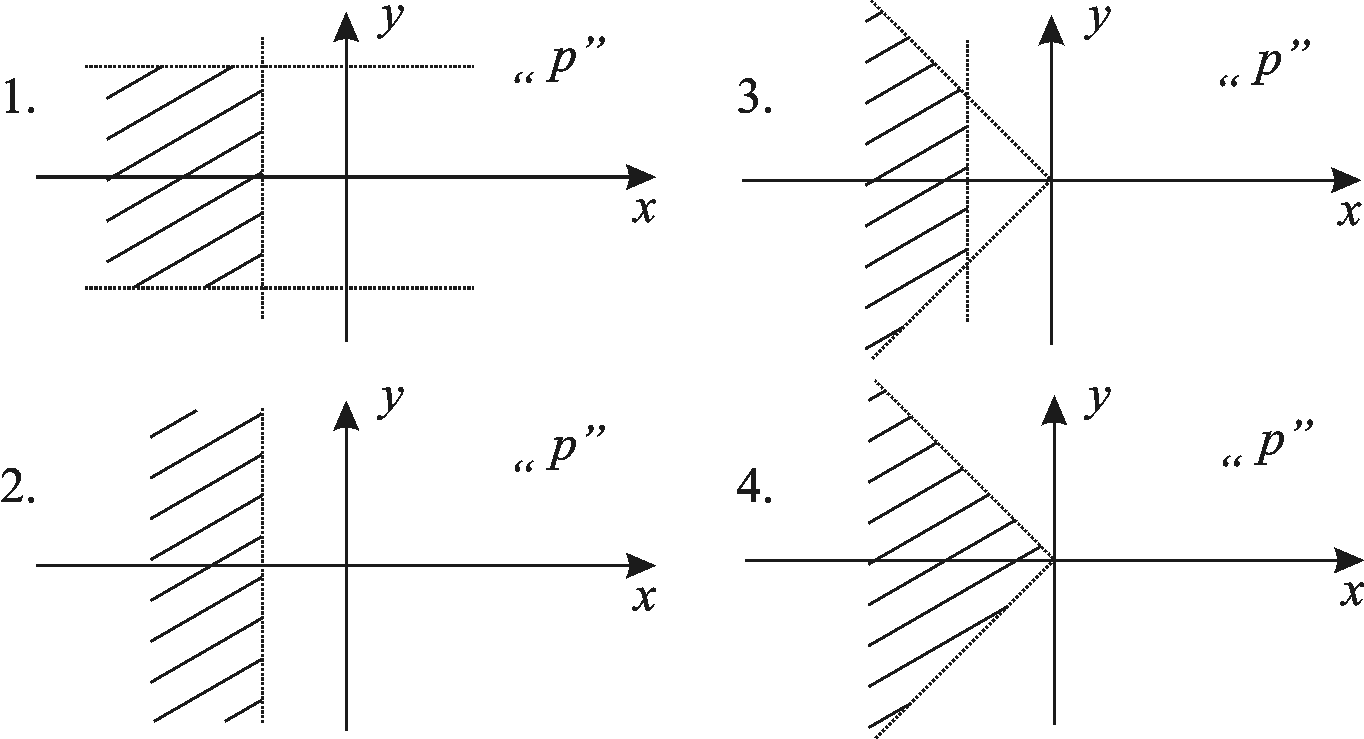 2
2
№25
В системе заданы ограничения на
колебательность
![]() ,
так что выполняется условие
,
так что выполняется условие![]() .При
этом область возможного расположения
корней характеристического уравнения
на комплексной плоскости «р» имеет
вид:
.При
этом область возможного расположения
корней характеристического уравнения
на комплексной плоскости «р» имеет
вид:
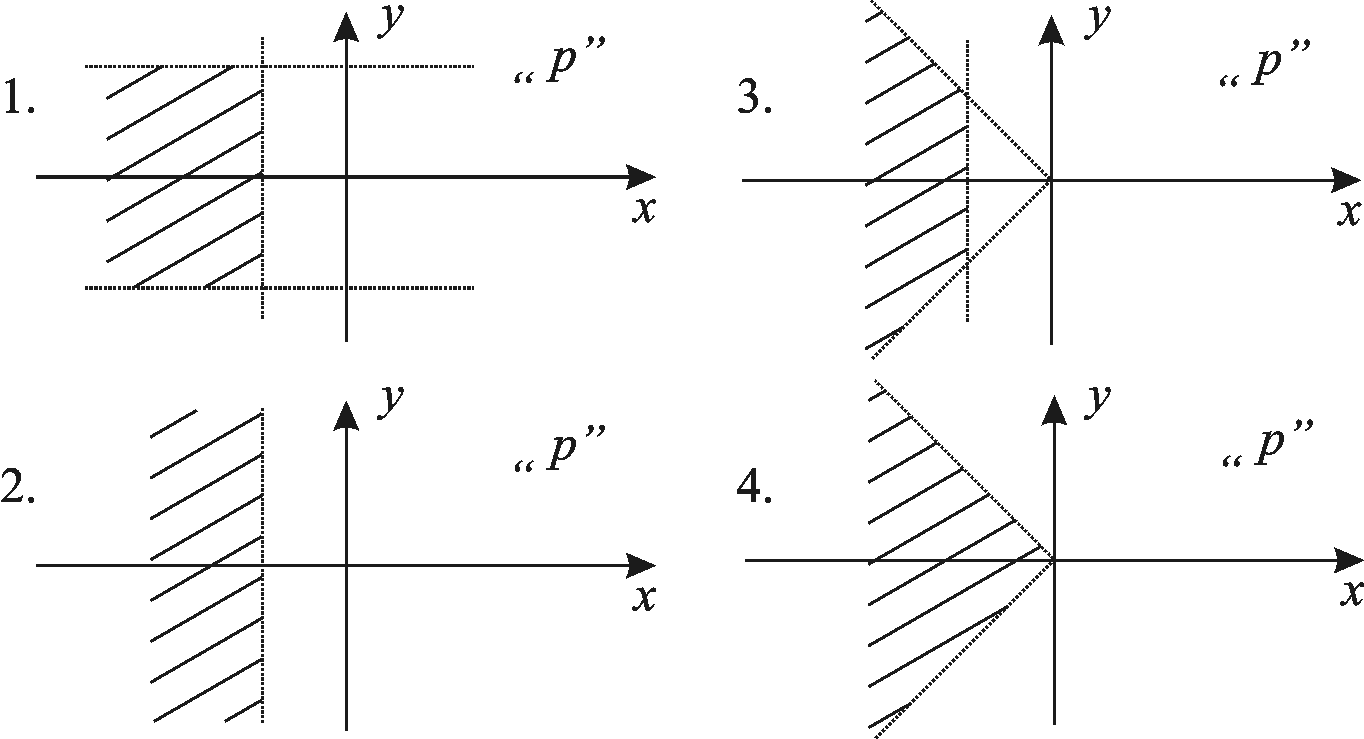 4
4
№26
Характеристическое уравнение системы
имеет следующие корни:
![]() .
Колебательность системы
.
Колебательность системы![]() равна:
равна:
1. 2 2. 16 3. 8 4. 4.
№27
Характеристическое уравнение системы
имеет следующие корни:
![]() .
Колебательность системы
.
Колебательность системы![]() равна:
равна:
1. 21 2. 7/33. 3/7 4. 7.
№28
При выборе нулей и полюсов передаточной
функции
![]() системы желательно:
системы желательно:
1. Удалять нули передаточной функции от полюсов.
2. Относительное расстояние нулей и полюсов не влияет на переходные процессы в системе.
3. Сближать нули и полюсы передаточной функции.
4. Удалять нули друг от друга.
Синтез
№1
Синтез САУ в данном курсе рассматривается как:
1. Решение некоторой вариационной задачи получения САУ, оптимальной по выбранному критерию качества.
2. Выбор всех составных частей системы, обеспечивающий выполнение некоторых требований.
3. Выбор всех элементов системы, за исключением объекта управления.
4. Определение структуры и параметров корректирующего устройства, добавляемого к неизменяемой части системы.
№2
Передаточная функция пропорционально-интегрального управляющего устройства имеет вид:
1.
![]() 3.
3.![]()
2.
![]() 4.
4.![]() .
.
№3
Передаточная функция ПИД - управляющего устройства имеет вид:
1.
![]() 3.
3.![]()
2.
![]() 4.
4.![]() .
.
№4
При использовании последовательного П – регулятора наблюдается (выделить неверное утверждение):
1. Увеличение точности системы.
2. Увеличение частоты среза.
3. Повышение быстродействия системы.
4. Увеличение запасов устойчивости системы.
№5
Передаточная функция изодромного управляющего устройства имеет вид:
1.
![]() 3.
3.![]()
2.
![]() 4.
4.![]() .
.
№6
При использовании последовательного И – регулятора наблюдается:
1. Повышение точности системы.
2. Увеличение частоты среза.
3. Повышение быстродействия системы.
4. Увеличение запасов устойчивости системы.
№7
При использовании последовательного ПИ – регулятора удается сохранить исходные запасы устойчивости за счет того, что:
1. ЛАФЧХ системы с ПИ регулятором отличаются от ЛАФЧХ исходной САУ только в высокочастотной области.
2. ЛАФЧХ системы с ПИ регулятором отличаются от ЛАФЧХ исходной САУ только в среднечастотной области.
3. ЛАФЧХ системы с ПИ регулятором отличаются от ЛАФЧХ исходной САУ только в низкочастотной области.
4. Использование ПИ – регулятора вносит положительный фазовый сдвиг в ЛФЧХ системы.
№8
При использовании последовательного ПИ – регулятора частота среза разомкнутой системы:
1. Существенно не меняется.
2. Становится существенно меньше частоты среза нескорректированной системы.
3. Становится существенно больше частоты среза нескорректированной системы.
№9
Основной целью использования последовательного ПД – регулятора является:
1. Повышение точности системы.
2. Увеличение запасов устойчивости.
3. Уменьшение влияния возмущающих воздействий.
4. Введение интеграла в закон управления.
№10
Основной чертой, отличающей ПД – закон управления от других, является:
1. Введение интеграла от ошибки в закон управления.
2. Введение ошибки в закон управления.
3. Введение производной ошибки в закон управления.
4. Введение линейной комбинации интеграла и производной в закон управления.
№11
В оптимальном процессе регулирования, используемом при синтезе, ограниченным является:
1. Время регулирования.
2. Перерегулирование.
3. Вторая производная управляемой величины.
4. Порядок астатизма системы.
№12
В системе
![]() - входной сигнал,
- входной сигнал,![]() -
максимальное ускорение управляемой
величины. В оптимальном переходном
процессе время регулирования определяется
как:
-
максимальное ускорение управляемой
величины. В оптимальном переходном
процессе время регулирования определяется
как:
1.
![]() 3.
2
3.
2![]()
2. 2![]() 4.
2
4.
2![]() .
.
№13
В системе
![]() - входной сигнал,
- входной сигнал,![]() -
максимальное ускорение управляемой
величины,
-
максимальное ускорение управляемой
величины,![]() - минимальное время отработки ступенчатого
входного сигнала. В оптимальном переходном
процессе эти величины связаны зависимостью:
- минимальное время отработки ступенчатого
входного сигнала. В оптимальном переходном
процессе эти величины связаны зависимостью:
1.
![]() 3.
3.![]()
2.
![]() 4.
4.![]() .
.
№14
В системе
![]() - входной сигнал,
- входной сигнал,![]() -
максимальное ускорение управляемой
величины. Частота среза оптимальной
системы определяется зависимостью:
-
максимальное ускорение управляемой
величины. Частота среза оптимальной
системы определяется зависимостью:
1.
![]() 3.
3.![]()
2.
![]() 4.
4.![]() .
.
№15
В желаемой ЛАЧХ наклон среднечастотной асимптоты равен –20дб/дек потому, что:
1. Он обеспечивает наилучшую точность системы.
2. Такой наклон имеет ЛАЧХ оптимальной системы.
3. При этом обеспечивается максимальное быстродействие.
4. При этом в синтезируемой системе отсутствует перерегулирование.
№16
При построении желаемой ЛАЧХ значение коэффициента передачи разомкнутой системы определяется, исходя из:
Необходимости обеспечения требуемого значения второй производной управляемой величины.
Необходимости обеспечения требуемого времени регулирования.
Необходимости обеспечения требуемого значения ошибки.
Необходимости обеспечения требуемого перерегулирования.
№17
При проведении синтеза коэффициент
передачи должен превышать некоторое
граничное значение
![]() .
Величина
.
Величина![]() задает:
задает:
1. Требуемое быстродействие системы.
2. Требуемую точность системы.
3. Требуемую устойчивость системы.
4. Требуемое перерегулирование системы.
№18
При синтезе входной сигнал
![]() ,
максимальное значение установившейся
ошибки
,
максимальное значение установившейся
ошибки![]() ,
система статическая. При построении
низкочастотной асимптоты выбор
коэффициента передачи разомкнутой
системы
,
система статическая. При построении
низкочастотной асимптоты выбор
коэффициента передачи разомкнутой
системы![]() осуществляется
из условия:
осуществляется
из условия:
1.
![]() 3.
3.![]()
2.
![]() 4.
4.![]() .
.
№19
Наклон низкочастотной асимптоты желаемой ЛАЧХ определяется:
1. Порядком астатизма исходной системы.
2. Равен![]() .
.
3. Заданным порядком астатизма скорректированной САУ.
4. Повторяет наклон низкочастотной части исходной системы.
№20
Высокочастотная часть желаемой ЛАЧХ:
1.
Имеет наклон ![]() .
.
2.
Имеет наклон![]() ,
где
,
где![]() заданный порядок астатизма скорректированной
системы.
заданный порядок астатизма скорректированной
системы.
3. Совпадает с высокочастотной частью ЛАЧХ исходной системы.
4. Совпадает с высокочастотной частью ЛАЧХ исходной системы или параллельна ей.
№21
При построении среднечастотной части
желаемой ЛАЧХ частота среза
![]() должна находиться в диапазоне:
должна находиться в диапазоне:
1.
![]() 3.
3.![]()
2.
![]() 4.
4.![]() ,
,
здесь
![]() - частота среза, определяемая по номограмме
Солодовникова,
- частота среза, определяемая по номограмме
Солодовникова,![]() -частота
среза оптимальной системы.
-частота
среза оптимальной системы.
№22
Величина
![]() ,
определяется по номограмме Солодовникова,
исходя из следующих требований к
скорректированной системе:
,
определяется по номограмме Солодовникова,
исходя из следующих требований к
скорректированной системе:
1. Точности в установившемся режиме.
2. Только из времени регулирования.
3. Только из величины перерегулирования.
4. Из времени регулирования и перерегулирования.
№23
Если при выборе частоты среза желаемой
ЛАЧХ
![]() оказалось, что
оказалось, что![]() (
(![]() - частота среза, определяемая по номограмме
Солодовникова,
- частота среза, определяемая по номограмме
Солодовникова,![]() -частота
среза оптимальной системы), то следует
выбирать частоту среза в соответствии
с условием:
-частота
среза оптимальной системы), то следует
выбирать частоту среза в соответствии
с условием:
1.
![]() 3.
3.![]()
2.
![]() 4.
4.![]()
№24
№25
Если при выборе частоты среза желаемой
ЛАЧХ
![]() нарушается условие
нарушается условие![]() (
(![]() -частота
среза оптимальной системы), то:
-частота
среза оптимальной системы), то:
1. Быстродействие системы не будет удовлетворять требованиям задания.
2. Перерегулирование не будет удовлетворять требованиям задания.
3. Вторая производная управляемой величины будет превосходить максимально возможное значение.
4. Не будут обеспечены требуемые запасы устойчивости.
№26
Если при выборе частоты среза желаемой
ЛАЧХ
![]() нарушается условие
нарушается условие![]() (
(![]() - частота среза, определяемая по номограмме
Солодовникова), то:
- частота среза, определяемая по номограмме
Солодовникова), то:
1. Вторая производная управляемой величины будет превосходить максимально возможное значение.
2. Не будут обеспечены требуемые запасы устойчивости
3. Быстродействие системы может не удовлетворять требованиям задания.
4. Точность системы может не удовлетворять требованиям задания.
№27
На основании каких данных при синтезе
определяются избыток амплитуды
![]() и избыток фазы
и избыток фазы![]() :
:
По известным
![]() и номограмме для перерегулирования и
времени регулирования.
и номограмме для перерегулирования и
времени регулирования.
По известному порядку астатизма скорректированной системы.
По известным
![]() и номограмме замыкания для вещественной
частотной характеристики замкнутой
системы.
и номограмме замыкания для вещественной
частотной характеристики замкнутой
системы.
По известной среднечастотной асимптоте желаемой ЛАЧХ.
№28
Обозначим
![]() - желаемая ЛАЧХ,
- желаемая ЛАЧХ,![]() -
располагаемая ЛАЧХ. ЛАЧХ последовательного
корректирующего устройства
-
располагаемая ЛАЧХ. ЛАЧХ последовательного
корректирующего устройства![]() определяется зависимостью:
определяется зависимостью:
1.
![]() 3.
3.![]()
2.
![]() 4.
4.![]() .
.
