
- •Теория принятия решений
- •Часть 2 нелинейное программирование, теория игр, многокритериальные задачи принятия решений
- •Введение
- •4. Нелинейное программирование
- •4.1. Характеристика задач
- •4.2. Условия оптимальности
- •4.3. Квадратичное программирование
- •4.4. Сепарабельное программирование
- •4.5. Задачи дробно-линейного программирования
- •4.6. Методы спуска
- •4.7. Методы одномерной минимизации
- •4.7.3. Метод деления интервала пополам
- •4.7.4. Метод золотого сечения
- •4.7.6. Метод первого порядка
- •4.8. Многомерный поиск безусловного минимума
- •4.8.1. Метод Гаусса – Зейделя (покоординатного спуска)
- •4.8.2. Метод Хука – Дживса (метод конфигураций)
- •4.8.3. Симплексный метод
- •4.8.4. Градиентные методы
- •4.8.6. Методы сопряженных направлений
- •4.8.7. Методы случайного поиска
- •Алгоритм с возвратом при неудачном шаге
- •Алгоритм с обратным шагом
- •Алгоритм наилучшей пробы
- •Алгоритм статистического градиента
- •4.8.8. Генетические алгоритмы
- •Исходная популяция
- •Результаты работы оператора скрещивания
- •Популяция первого поколения
- •4.9. Методы условной оптимизации
- •4.9.2. Метод проектирования градиента
- •4.9.3. Метод штрафных функций
- •Минимизация по методу Ньютона
- •4.9.4. Метод барьерных функций
- •Результаты поиска алгоритмом барьерных функций
- •4.9.5. Другие методы условной оптимизации
- •5. Методы теории игр в управлении
- •5.1. Теория игр в контексте теории принятия решений
- •5.2. Матричные игры с нулевой суммой
- •Использование линейной оптимизации при решении матричных игр. Пусть игра не имеет оптимального решения в чистых стратегиях, т.Е. Седловая точка отсутствует .
- •5.3. Игры с природой
- •5.4. Критерии, используемые для принятия решений
- •В играх с природой. Критерии, основанные
- •На известных вероятностях стратегий природы
- •Иногда неопределенность ситуации удается в некоторой степени ослабить с помощью нахождения вероятностей состояний на базе данных статистических наблюдений.
- •5.5. Оценка необходимости эксперимента
- •6. Многокритериальные задачи принятия решений
- •6.1. Основы многокритериальный оптимизации
- •6.2. Принцип оптимальности Парето.
- •6.3. Принцип равновесия по Нэшу
- •6.4. Конфликты, переговоры и компромиссы
- •6.5. Краткий обзор методов решения задачи векторной оптимизации
- •Значения компонентов вектор-функции
- •1. Оптимальность по Парето
- •Исходные данные для задачи оптимизации по Парето
- •Эффективность операции
- •2. Принятие решений в условиях неопределенности
- •Исходные данные для задачи принятия решения в условиях неопределенности
- •3. Многокритериальная оптимизация
- •Заключение
- •Библиографический список
- •Оглавление
- •Теория принятия решений
4.8.2. Метод Хука – Дживса (метод конфигураций)
В методе Хука – Дживса каждая итерация состоит из двух фаз:
1) исследующего поиска;
2) движения по образцу (ускоряющего шага).
Исследующий поиск аналогичен одному циклу покоординатного спуска. Конечную точку цикла называют базовой. Две последовательные базовые точки определяют направление поиска на 2-й фазе. Точка, получаемая в результате ускоряющего шага, называется временной. Начальная точка одновременно является базовой и временной.
Сначала
приведем вариант метода, предложенный
Хуком и Дживсом и описываемый в
литературе под названием «метод
конфигураций». В нем используются только дискретные
шаги. Процедура поиска показана на рис.
4.21. Из начальной точки X(0)
делается шаг
по x1
в одну сторону и, если успешно, то
значение фиксируется, иначе направление
шага изменяется на противоположное.
Также делается по остальным
координатам. Итогом первого
исследующего поиска является точка
X(1).
В направлении X(1)
– X(0)
осуществляется движение по образцу,
дающее временную точку Y(1)
=
= X(1)
+ (X(1)
– X(0)),
где
– коэффициент ускорения (рекомендуется
брать от 1 до 2). Из полученной временной
точки снова проводится исследующий
поиск, приводящий в очередную базовую
точку X(2).
Ускоряющий шаг в направлении X(2)
– X(1)
дает временную точку Y(2).
Фазы поиска повторяются без изменения
величины шага, если f(Y(k))
< f(X(k)).
В противном случае, если
< ,
поиск заканчивается и X(k)
принимается за решение, а иначе следует
положить Y(k)
= X(k),
уменьшить шаг в два раза и перейти к
исследующему поиску из точки Y(k).
нем используются только дискретные
шаги. Процедура поиска показана на рис.
4.21. Из начальной точки X(0)
делается шаг
по x1
в одну сторону и, если успешно, то
значение фиксируется, иначе направление
шага изменяется на противоположное.
Также делается по остальным
координатам. Итогом первого
исследующего поиска является точка
X(1).
В направлении X(1)
– X(0)
осуществляется движение по образцу,
дающее временную точку Y(1)
=
= X(1)
+ (X(1)
– X(0)),
где
– коэффициент ускорения (рекомендуется
брать от 1 до 2). Из полученной временной
точки снова проводится исследующий
поиск, приводящий в очередную базовую
точку X(2).
Ускоряющий шаг в направлении X(2)
– X(1)
дает временную точку Y(2).
Фазы поиска повторяются без изменения
величины шага, если f(Y(k))
< f(X(k)).
В противном случае, если
< ,
поиск заканчивается и X(k)
принимается за решение, а иначе следует
положить Y(k)
= X(k),
уменьшить шаг в два раза и перейти к
исследующему поиску из точки Y(k).
Модификация метода Хука – Дживса заключается в замене дискретных шагов одномерной минимизацией. В этом варианте исследующий поиск полностью совпадает с одним циклом покоординатного спуска, т.е. по каждой координате выполняются не дискретные шаги, а ищется минимум. При движении по образцу также ищется минимум функции только по одной неизвестной – коэффициенту ускорения :
![]()
По оптимальному значению * определяется временная точка
![]() .
.
Поиск завершается, когда расстояние между двумя смежными базовыми точками становится меньше заданной величины:
![]() .
.
К этому условию можно добавить и требование по точности функции:
![]()
4.8.3. Симплексный метод
В симплексном методе движение к минимуму осуществляется с использованием симплекса – выпуклого многогранника с числом вершин на единицу больше размерности пространства. Примером симплекса на плоскости является любой треугольник, в трехмерном пространстве – пирамида с треугольником в основании.
С имплекс
обладает замечательным свойством: если
взять только одну точку вне симплекса
в качестве новой вершины, то, соединив
ее с вершинами прилежащей грани, получим
новый симплекс. На рис. 4.22 слева из
исходного симплекса с вершинами 1, 2, 3
построено 2 других симплекса, а справа
новый симплекс построен на грани 2, 3, 4
исходного и новой вершины 5.
имплекс
обладает замечательным свойством: если
взять только одну точку вне симплекса
в качестве новой вершины, то, соединив
ее с вершинами прилежащей грани, получим
новый симплекс. На рис. 4.22 слева из
исходного симплекса с вершинами 1, 2, 3
построено 2 других симплекса, а справа
новый симплекс построен на грани 2, 3, 4
исходного и новой вершины 5.
Очевидно, что если взять одну из вершин симплекса, то все остальные вершины будут на противолежащей грани симплекса. Эти свойства справедливы для любой размерности пространства.
З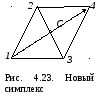 ная
значения функции в вершинах симплекса,
легко определить направление, в котором
функция может улучшиться. В этом
направлении строится новый симплекс:
определяется самая худшая вершина (по
значению функции) и она отражается через
центр противолежащей грани, как показано
на рис. 4.23. В построенном симплексе
значение функции неизвестно только в
вершине 4. Таким образом, после построения
нового симплекса функция вычисляется
всего один раз при любой размерности
пространства. Лишь в начальном симплексе
необходимо вычислять функцию во всех
вершинах.
ная
значения функции в вершинах симплекса,
легко определить направление, в котором
функция может улучшиться. В этом
направлении строится новый симплекс:
определяется самая худшая вершина (по
значению функции) и она отражается через
центр противолежащей грани, как показано
на рис. 4.23. В построенном симплексе
значение функции неизвестно только в
вершине 4. Таким образом, после построения
нового симплекса функция вычисляется
всего один раз при любой размерности
пространства. Лишь в начальном симплексе
необходимо вычислять функцию во всех
вершинах.
Последовательное отражение наихудших вершин перемещает симплекс в направлении уменьшения значения функции, что в конечном итоге приводит к отысканию минимума с заданной точностью. Характер движения симплекса представлен на рис. 4.24.

Рис. 4.24. Характер движения симплекса
Отражение вершин показано пунктирными линиями. Сначала отражается вершина 1, затем в полученном симплексе отражается вершина 3, симплекс 2, 4, 5 заменяется на 4, 5, 6 и т.д. Очевидно, что в процессе движения, особенно вблизи экстремума, новая вершина может оказаться не лучше отраженной. Для предотвращения зацикливания либо отражается другая вершина, либо уменьшается размер нового симплекса.
Рассмотрим
вычислительную сторону метода. В качестве
начального симплекса обычно берется
регулярный симплекс. Регулярность
означает равенство длин всех ребер. Он
строится следующим образом. Начальная
точка
![]() принимается за базовую вершину,
относительно которой располагаются
остальные вершины.
принимается за базовую вершину,
относительно которой располагаются
остальные вершины.
Их координаты вычисляются по формуле

где i – номер вершины; j – координата вершины (индекс переменной); n – число переменных (размерность пространства), а приращения 1 и 2 зависят от n и выбранного масштабного множителя :
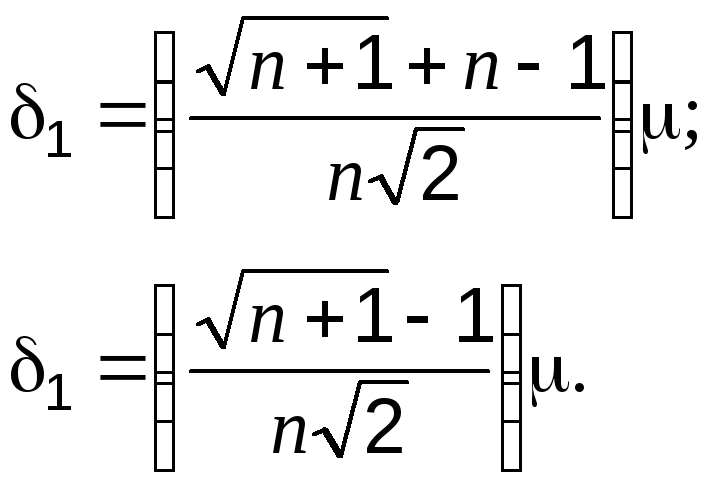
При =1 все ребра имеют единичную длину.
Вычисление координат новой вершины, получающейся в результате отражения одной из вершин последнего симплекса, производится следующим образом. Пусть отражается вершина k (например, вершина 1 на рис. 4.24). Тогда сначала определяется центр противолежащей грани C
![]()
а затем координаты новой вершины s:
x(s) = x(k) + (xC – x(k)),
или
x(s) = xС + (xC – x(k)), (4.42)
где > 0 и – параметры отражения.
Предложен целый ряд методов, основанных на поиске по симплексам, отличающихся способом построения очередного симплекса и значениями параметров отражения. Лучшим из них считается метод Нелдера – Мида. В нем заложено гибкое управление симплексом, при котором он может как уменьшаться, так и увеличиваться, приспосабливаясь к поверхности функции. Оно использует 3 варианта отражения с соответствующими параметрами:

Значения коэффициентов отражения были подобраны экспериментально: = 1; = 0,5; = 2. Предложены и другие наборы значений, однако они дают лучшие результаты только в частных случаях.
В алгоритме Нелдера – Мида используются три вершины: А – с наибольшим значением целевой функции (худшая); В – со следующим значением и L – с наименьшим значением (лучшая). Всегда отражается вершина А.
С начала
производится нормальное отражение.
Получаемая в результате точкаD
считается временной (рис. 4.25). Далее идут
проверки:
начала
производится нормальное отражение.
Получаемая в результате точкаD
считается временной (рис. 4.25). Далее идут
проверки:
если fL < fD < fB, нормальное отражение приемлемо и временная точка фиксируется;
если fB fD < fA, то выполняется сжатие с = и фиксируется точка Db;
если fD fА, симплекс сжимается с = – и фиксируется точка D–b;
если fD < fL, то производится растяжение ( = ), дающее точку Dg, которая фиксируется, если она не хуже временной; иначе она не учитывается и фиксируется временная точка.
В условии останова поиска может использоваться показатель размера симплекса, например, максимальная длина ребра и/или разность значений целевой функции fА– fL.
Метод характеризуется как эффективный. Он мало чувствителен к помехам или ошибкам при определении значений целевой функции, так как определяющими являются отношения значений, а не абсолютные величины. Благодаря изменению размеров симплекса он может работать в условиях «оврага».
И нтересен
вариант метода, в котором на всех
итерациях симплекс остается регулярным.
В нем используется коэффициент уменьшения
длины ребраβ 0,85.
Симплекс сжимается, стягиваясь к
лучшей вершине, как показано на рис.
4.26, и после этого происходит
отражение. Такое значение β
обусловлено тем, что на вершины
уменьшенного симплекса переносятся
значения функции соответствующих вершин
до сжатия. Тем самым исключаются
дополнительные вычисления функции.
Возможно также увеличение симплекса
за счет удлинения всех ребер с
коэффициентом 1/β
при сохранении
положения наихудшей вершины.
нтересен
вариант метода, в котором на всех
итерациях симплекс остается регулярным.
В нем используется коэффициент уменьшения
длины ребраβ 0,85.
Симплекс сжимается, стягиваясь к
лучшей вершине, как показано на рис.
4.26, и после этого происходит
отражение. Такое значение β
обусловлено тем, что на вершины
уменьшенного симплекса переносятся
значения функции соответствующих вершин
до сжатия. Тем самым исключаются
дополнительные вычисления функции.
Возможно также увеличение симплекса
за счет удлинения всех ребер с
коэффициентом 1/β
при сохранении
положения наихудшей вершины.
