4.7.4. Метод золотого сечения

Золотое сечение – это определенное отно­ше­ние части к целому. Отрезок АВ делится точ­кой С в отношении золотого сечения (рис. 4.11), если

. (4.37)

Положим АВ = 1, АС = х, СВ = 1 – х, тогда из выражения (4.37) получаем уравнение

х² + х – 1 = 0,

из которого следует

;

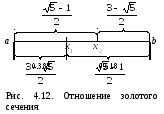
Эти отношения используются для выбора двух точек внутри интервала неопределенности. Они располагаются, как показано на рис. 4.12. Каждая из точек делит интервал [a, b] в отношении золотого сечения.

В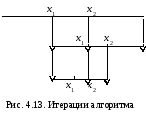этих точках вычисляется функция. Еслиf(x₁) > f(x₂), то отбрасывается часть ин­тер­вала [a, x₁], если f(x₁) < f(x₂), то отсекается часть [x₂, b], а при равенстве значений функ­ции – любая из них. Оставшаяся часть ин­тервала равна от величины ис­ход­ного. Очевидно, что после такого сокра­ще­ния интервала одна из внутренних точек остается с изменением индекса, а вторая берется на основе золотого сечения или, что одно и то же, симметрично оставшейся (рис. 4.13). Сокращение интервала продолжается до достижения заданной точности.

Алгоритм

1. Задать точность по координате .

2. Вычислить

3. Вычислить f( x₁), f( x₂).

4. Если f(x₁) > f(x₂), положить a = x₁, x₁ = x₂, 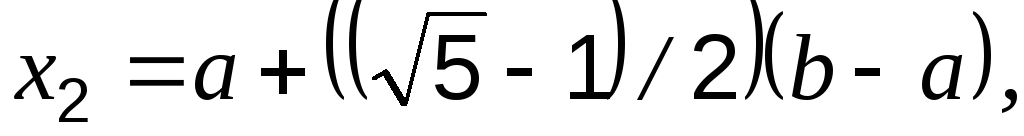или x₂ = a + b – x₁, иначе – b = x₂, x₂ = x₁, или x₁ = a + b – x₂.

5. Если (b – a) < , закончить поиск.

6. Вычислить функцию в новой точке и перейти на п. 4.

Итерации алгоритма графически иллюстрируются на рис. 4.13.

Покажем, что сохраняемая точка (x₁ или x₂) делит сокращенный интервал также в отношении золотого сечения. Пусть на k-й итерации внутренние точки делят интервал [a^k, b^k] в отношении золотого сечения. Обозначив = b^k – a^k, , имеем

.

Тогда для нового, сокращенного, интервала находим

;

В результате получаем

.

Благодаря этому свойству внутренние точки не сливаются при любом числе итераций.

Согласно алгоритму функция вычисляется 2 раза на начальном интервале и по одному разу на всех последующих. Поэтому после n вычислений функции интервал неопределенности составит от величины первоначального. При заданной точности можно найти необходимое количество вычислений функции n из условия

4.7.5. Метод Фибоначчи

Схема метода Фибоначчи почти полностью совпадает с методом золотого сечения. Отличие в том, что вместо золотого сечения используется отношение чисел Фибоначчи: на k-й итерации доли малого и большого отрезков интервала равны и соответственно.

Числа Фибоначчи F_ вычисляются по известным соотношениям: F₀ = F₁ = 1; F_ = F_{ –1} + F_{ –2};   2.

Точки x₁ и x₂ вычисляются по формулам:

; (4.38)

. (4.39)

Как очевидно, они идентичны приведенным выше (см. п. 4.7.4). Однако если при использовании золотого сечения внутренние точки не могут сливаться, то здесь это не так. Действительно, при k = n – 1 из формул (4.38) и (4.39) имеем

; .

Но так как F₀/F₂ = F₁/F₂ = 1/2, то , и, следовательно, точки сливаются в середине интервала. Поэтому до начала итераций необходимо определить значение n, гарантирующее достижение минимума с заданной точностью . После 1-й итерации длина интервала составит от величины исходного, после 2-й – ()(), …, после (n–1)-й –

.

Значит, длина последнего интервала будет равна (b₁ – a₁)/F_n, где [a₁, b₁] – исходный интервал. Для обеспечения заданной точности требуется, чтобы

, или . (4.40)

Таким образом, соотношение (4.40) позволяет определить номер числа Фибоначчи по исходным данным. На начальном интервале точки вычисляются по формулам (4.38) и (4.39) при k = 1. На последующих итерациях числа Фибоначчи не требуются, так как одна точка переносится из предшествующей итерации, а вторая берется симметрично ей, т.е. лучше использовать вторые формулы из п. 4 алгоритма золотого сечения.

После слияния внутренних точек остается неопределенность с положением минимума. Для ее устранения вторая точка берется слева или справа от центра на расстоянии₁  (0,010,05). Для случая сдвига второй точки влево (рис. 4.14) при f(x₁) < f(x₁ – ₁) минимум лежит в интервале (2), в противном случае – в интервале (1).

Метод Фибоначчи является самым эффективными из всех прямых методов. Очень близок к нему метод золотого сечения: при n > 9 они практически совпадают по эффективности, и чем больше n, тем ближе эти методы. А в пределе отношение, используемое в методе Фибоначчи на 1-й итерации, становится равным золотому сечению:

.