Калинин / Приборостроителям / Математика 1 (15)

2.2

Подстановка , откуда ; ; .

=

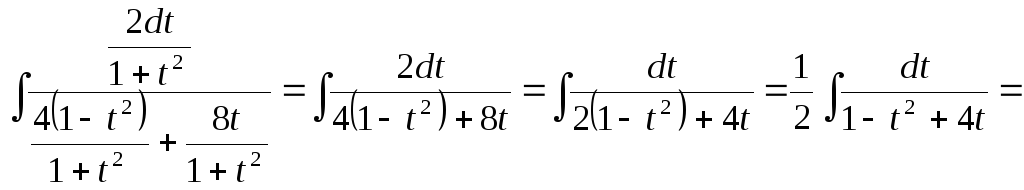
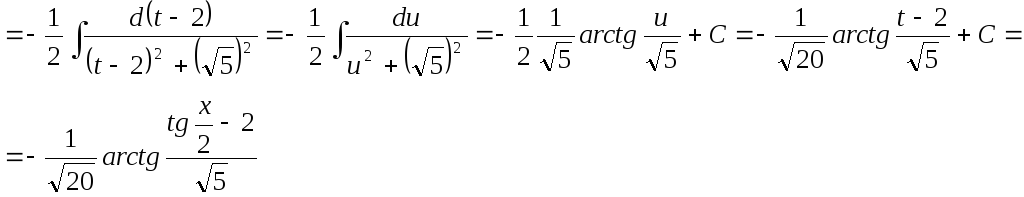1а)

Берем интегралы по отдельности:

1)

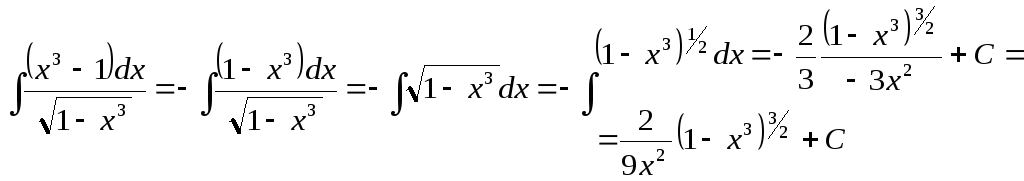
2)

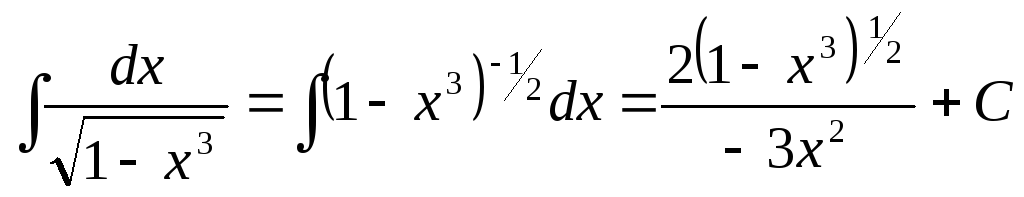
Окончательно .

2.б) .

2.в)

Имеем следующее разложение этой подынтегральной дроби на элементарные:

.

Откуда; ; ; .

Тогда

2.б)

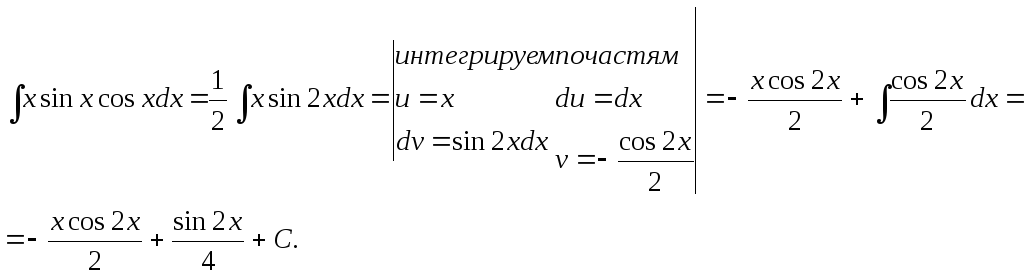
2.а) , учитывая, что , вводим замену .

Получили уравнение, в которое входят искомый интеграл и функция, выражая, получаем:

.

1.в) .

Разлагаем подынтегральную дробь на элементарные:

.

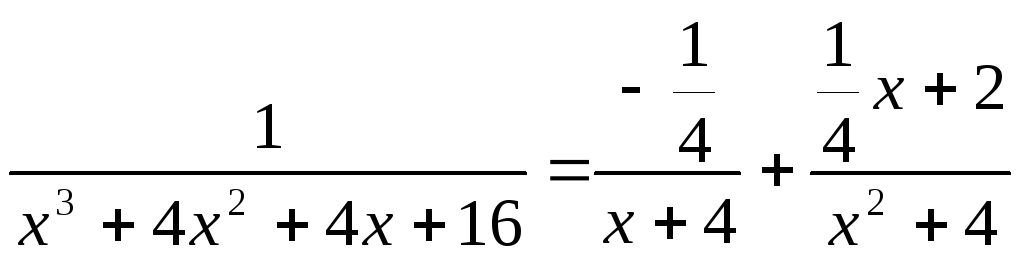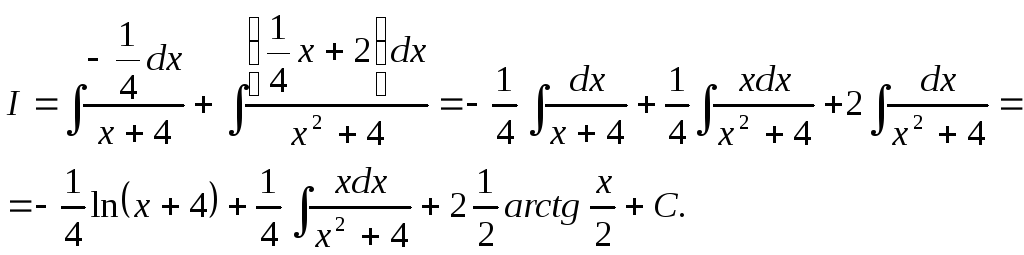
Берем интеграл отдельно

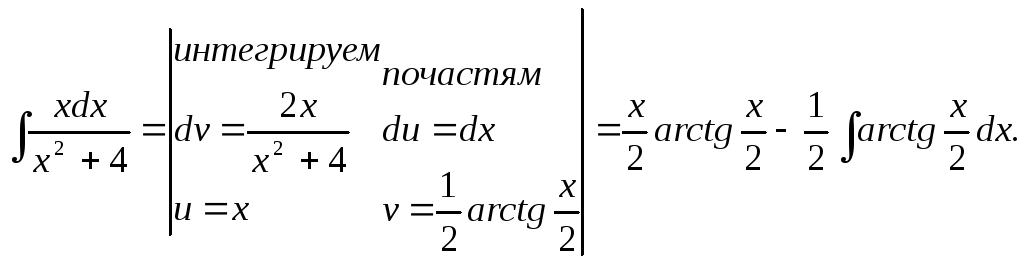
Берем интеграл отдельно:

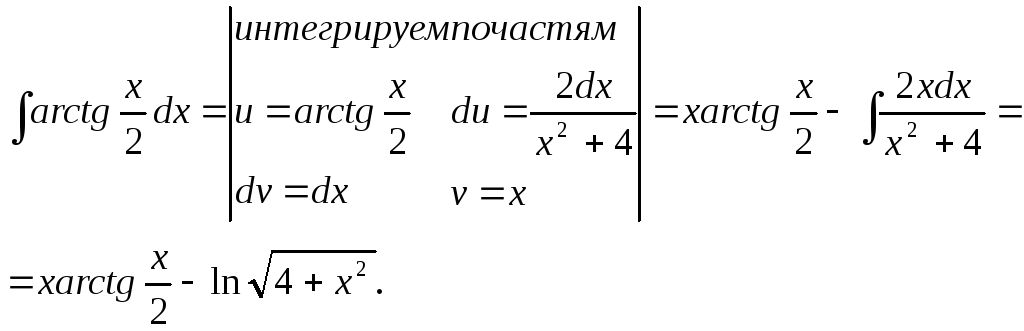
Окончательно:

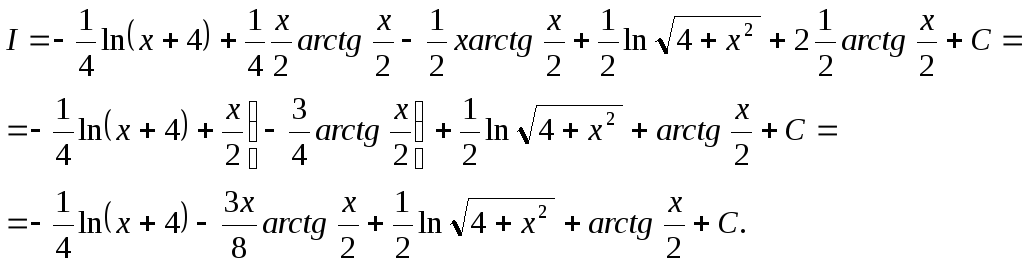
1.2)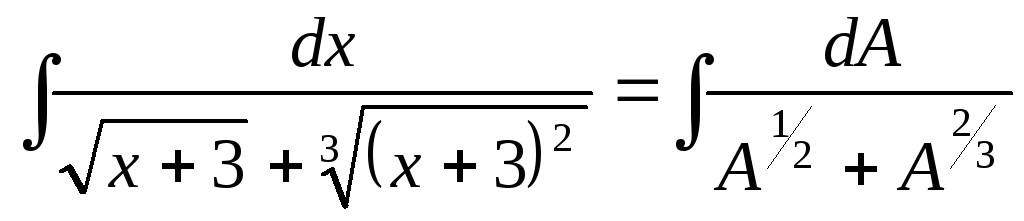; где

.

Берем интегралы по отдельности:

Тогда окончательно:

III а)

При x=0 уравнение выражается ; .

- частное решение диф.ур.

III б) .

При х=0, уравнение вырождается

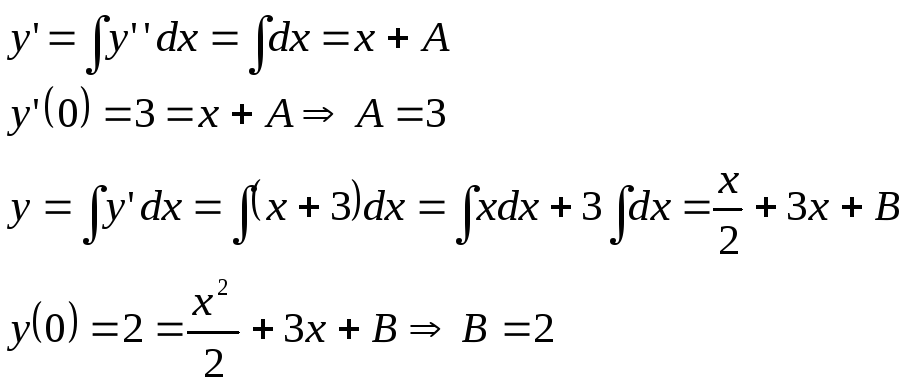
- частное решение диф.ур.

I.а) .

1) ОДЗ – функция определения на всей числовой прямой, кроме точек х=±1, где знаменатель обращается в нуль. В этих точках функция прерывна. На всей остальной числовой прямой она непрерывна.

2) Функция четная т.к. . Например,

3) Функция имеет точку экстремума

Соответственно, имеется четыре интервала монотонности функции

и .

4)

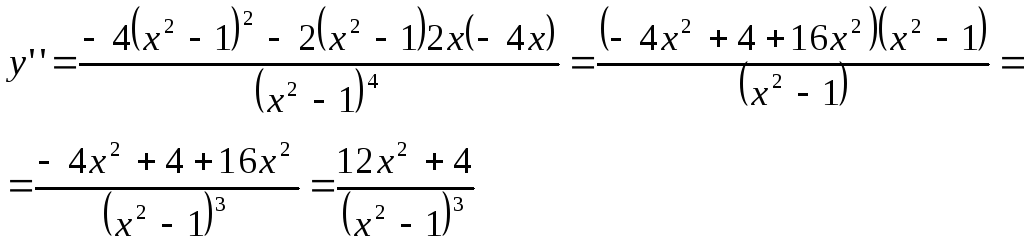
- не имеет действительных корней.

Таким образом, функция не имеет точек перегиба на ОО:

при - функция вогнута.

при - функция выпуклая.

Функция вогнутая на

Функция выпуклая на .

Точки перегиба в точках разрыва х=-1 и х=1.

5) Определение знаков интервалов монотонности и возрастания (убывания) функции на них.

- возрастает

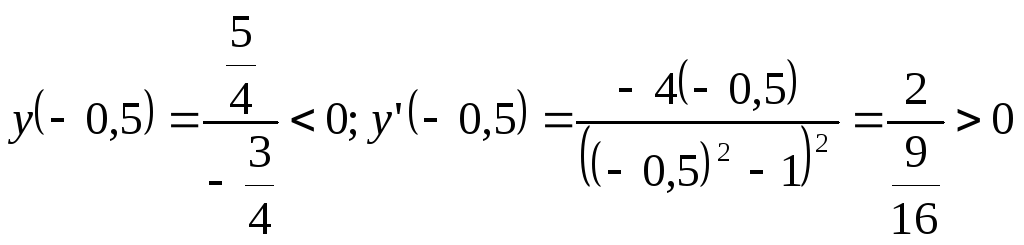- возрастает

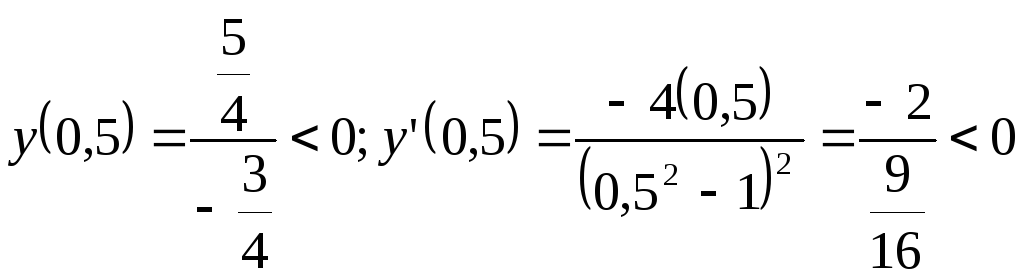- убывает

- убывает.

Точки пересечения с осями координат:

не пересекает ось х на области определения (ОО):

т.к. в т. Х=0 происходит смена знака с производной с + на -, то т. x=0; y=-1 – точка максимума.

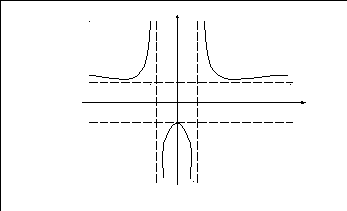
6) Определение асимптот графика функции:

вертикальные асимптоты х=-1 и х=1.

Ищем наклонные асимптоты.

При получаем:

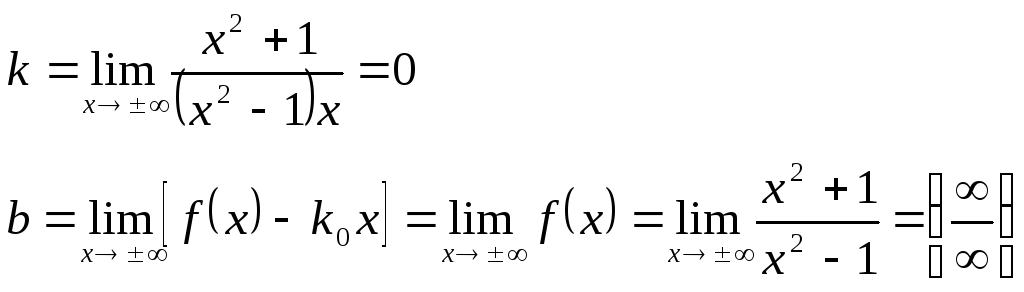
Применяя правило Лопиталя-Бернули дважды получаем:

- горизонтальная асимптота.

Построение графика функции:

I.б)

1) ОДЗ (00) – функция определения на всей числовой, за исключением точки х=1, где знаменатель обращается в нуль. В этой точке функция прерывна. На всей области определения функция непрерывна.

2) Функция ни четная, ни нечетная, т.к не выполняются равенства:

т.к.

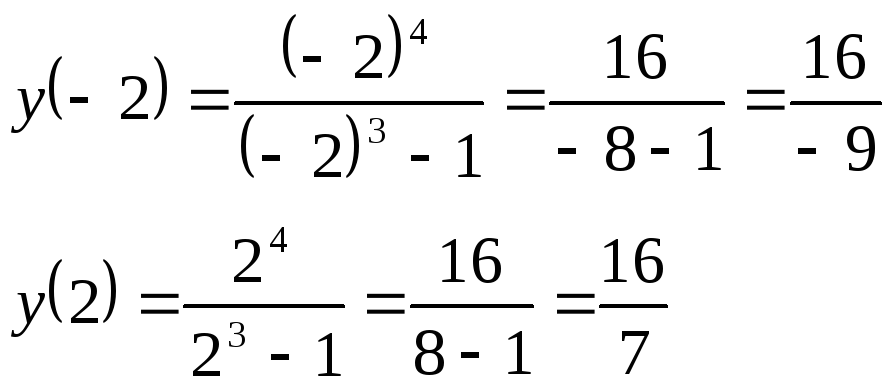
3) Функция имеет точки экстремума

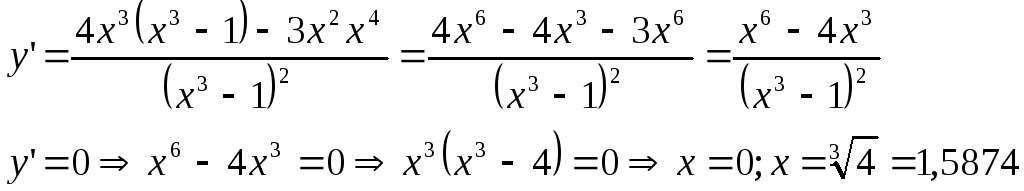
Соответственно имеется три интервала монотонности.

- функция возрастает

- функция убывает

- функция возрастает.

Соответственно - максимум

- минимум.

4)

или

Имеется три интервала выпуклости и вогнутости.

- выпукла

- вогнута

- вогнута.

Точка пересечения с осями координат

6) Определение асимптот графика функции:

вертикальная асимптота: х=1.

Ищем наклонные асимптоты

Применяем правило Лопиталя –Бернулли трижды получаем

Следовательно, правой асимптотой является прямая

Аналогично,

(также трижды применяем правило Лопиталя-Бернулли для раскрытия неопределенности).

Левой асимптотой является прямая

х