Калинин / Приборостроителям / Математика 1 (10)

Контрольная

1.Найти производную первого порядка, используя правила дифференцирования.

1.11

а) , рассмотрим как степенную функцию и найдём производную непосредственно:

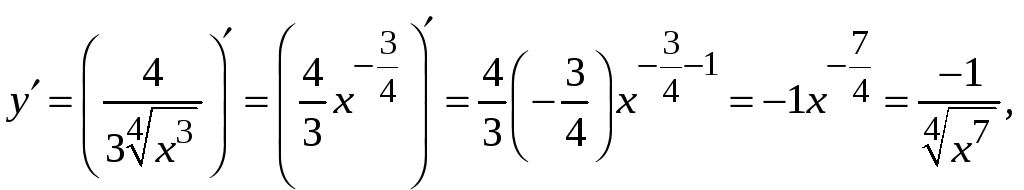
б) рассмотрим функцию как сложную и найдём производную по правилам нахождения производной для сложных функций:

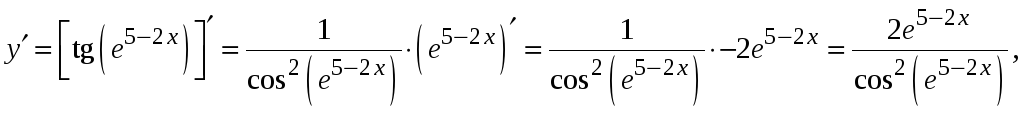
в) рассмотрим функцию как произведение двух сложных функций и воспользуемся правилами нахождения производной от произведения двух функций и правила дифференцирования сложной функции, причём производная от второй функции, входящей в произведение нам уже известна (см. п. б):

2. Найти дифференциал первого порядка.

2.11

дифференциал первого порядка это первая производная функции по аргументу, умноженная на бесконечно малое приращение аргумента:

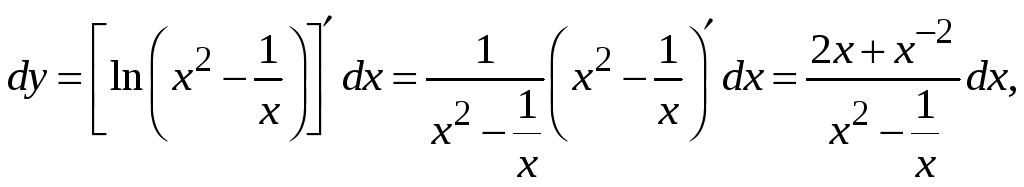
3. найти производную второго порядка.

3.11

, рассмотрим функцию как сумму двух функций, одна из которых сложная, и найдём первую производную непосредственно, а вторую – как производную от произведения функций, одна из которых сложная:

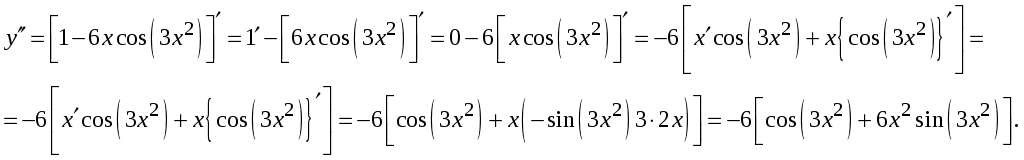
4. Исследовать функцию и построить ее график.

4.11

1) Область определения функции – всё множество действительных чисел;

2) Область значений функции - всё множество действительных чисел;

3) С осью OY функция пересекается в точке (0, 0), с осью ОХ в точках (-2, 0); (0, 0); (2, 0).

4) Интервалы знакопостоянства: на объединении интервалов (-∞, -2) и (0, 2) значения функции отрицательны; на объединении интервалов (-2, 0) и (2, ∞) значения функции положительны.

5) Функция имеет стационарные точки:

6) Интервалы монотонности: на объединении интервалов () и () функция возрастает, на интервале () – убывает.

7) Точки перегиба – это точки, в которых вторая производная равна нулю:

8) Точки экстремума: стационарные точки функции, в которых вторая производная отлична от нуля являются точками экстремума:

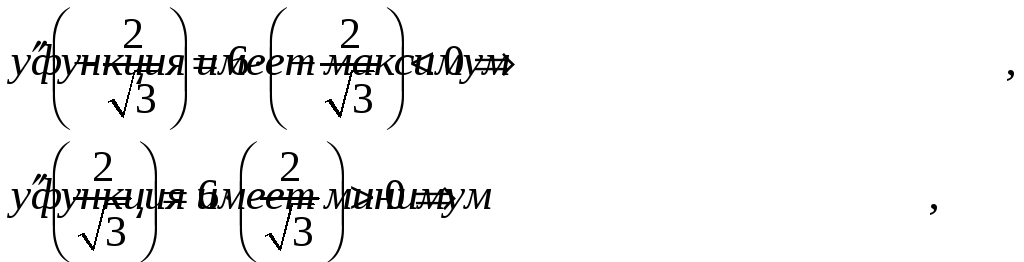
9) Вертикальных асимптот функция не имеет, так как нет разрывов в области определения, горизонтальных и наклонных асимптот функция не имеет, так как при приближении к минус бесконечности функция неограниченно убывает ,а при приближении к плюс бесконечности неограниченно возрастает.

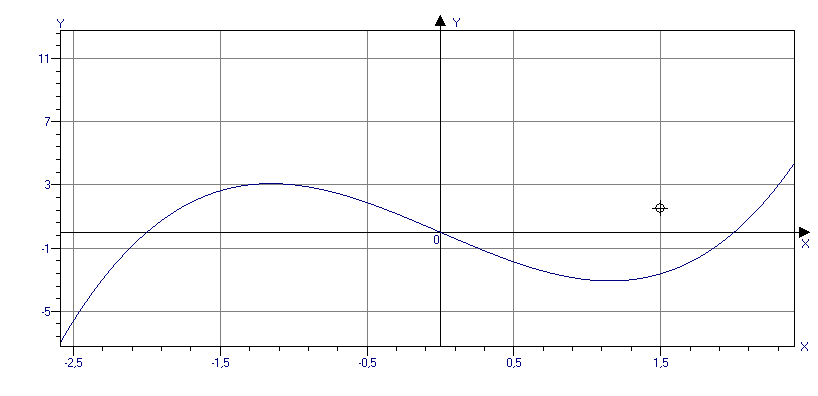
График функции:

5.найти неопределенный интеграл.

5.11

а) раскроем все скобки в подынтегральном выражении и вычисли интеграл непосредственно как интеграл от суммы:

б) вычислим интеграл, произведя замену :

6. вычислить определенный интеграл.

6.11

вычислим интеграл, произведя замену :

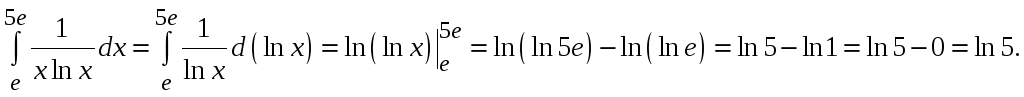
7. практические приложения дифференциального и интегрального исчисления.

7.11

Задача 1. Тело массой 6 г движется по закону Определить кинетическую энергию тела через 5 с после начала движения.

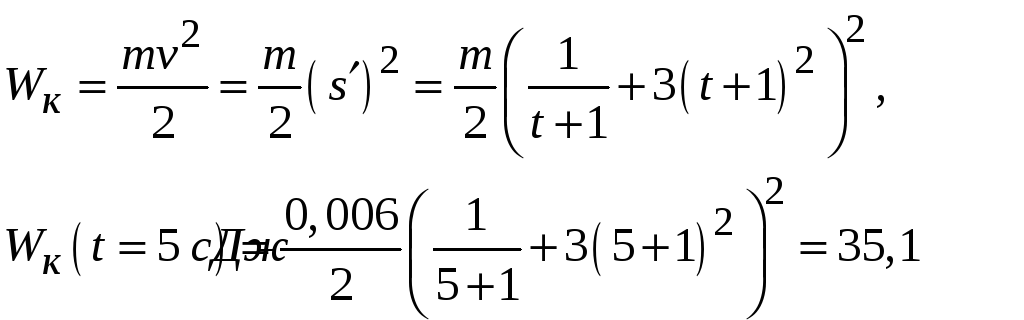
Задача 2. Реакция организма на введённый лекарственный препарат описывается функцией где х – доза лекарственного препарата, а – положительная постоянная. При каком значении х реакция максимальна?

Реакция организма будет экстремальной (минимальной или максимальной) при тех значениях х, при которых функция реакции организма принимает экстремальное значение.

Исследуем функцию реакции на экстремум:

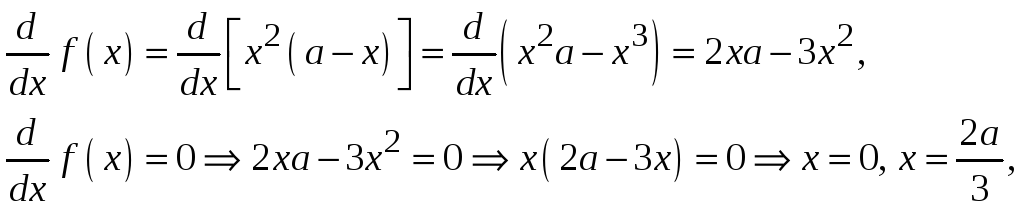
Максимальное значение функции достигается в той стационарной точке, в которой вторая производная отрицательна:

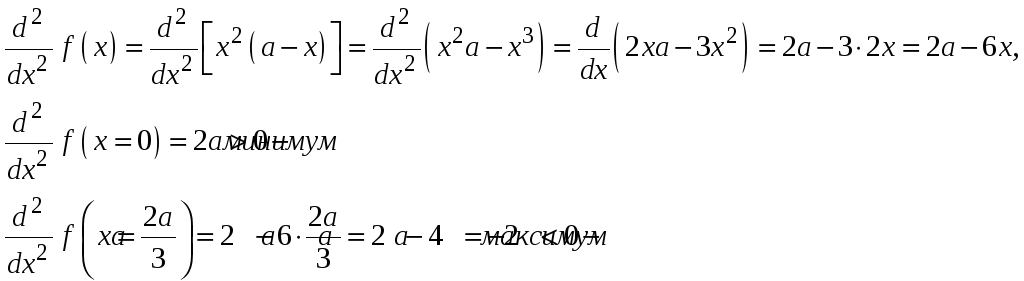
Ответ: реакция организма на лекарственный препарат максимальна при х=2а/3.

Задача 3. Материальная точка движется прямолинейно. Ускорение точки изменяется по закону где А=8 м/с², В=4 м/с³, С=14 м/с⁴. Какой скорости достигнет материальная точка через 0,4 с после начала движения из состояния покоя? Какой путь пройдёт она за это время?

Скорость точки при переменном ускорении равна интегралу от ускорения по времени, а пройденный путь – интегралу по времени, взятому дважды:

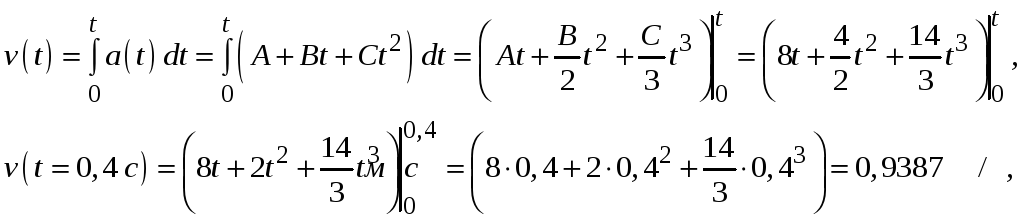
За это время будет пройден путь: