Калинин / Приборостроителям / Математика 1 (1)

Контрольная работа № 2

1. Найти неопределённый интеграл

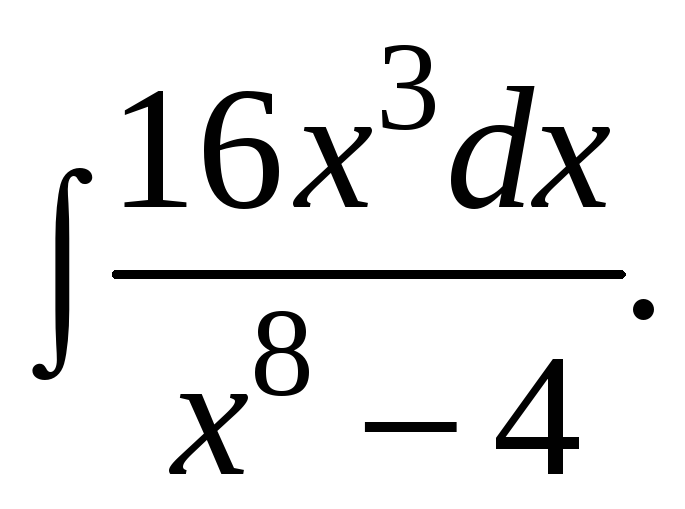
Решение

Разложим подынтегральную дробь на элементарные и проинтегрируем.

Разложим на элементарные дроби вида:

Приведём дроби к одному знаменателю и приведём подобные члены:

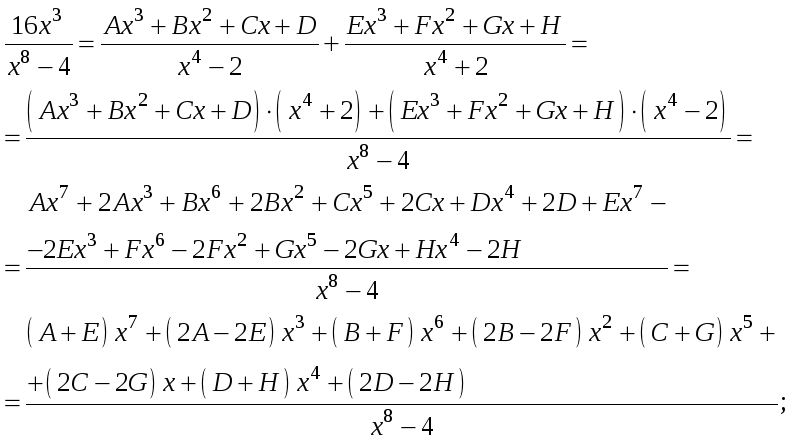
Приравнивая скобки при всех степенях, кроме нулю, получаем:

Отсюда получаем:

Тогда

2. Вычислить определённый интеграл

Решение

Интегрируем непосредственно:

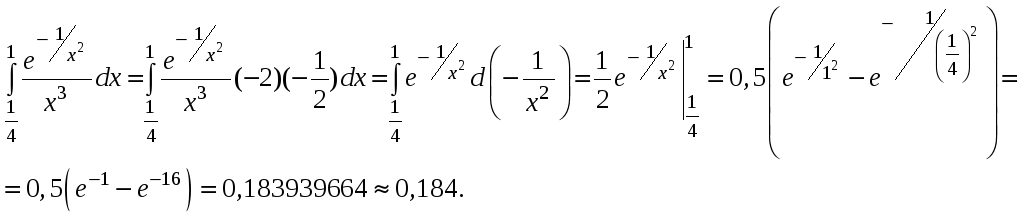
3. Вычислить определённый интеграл :

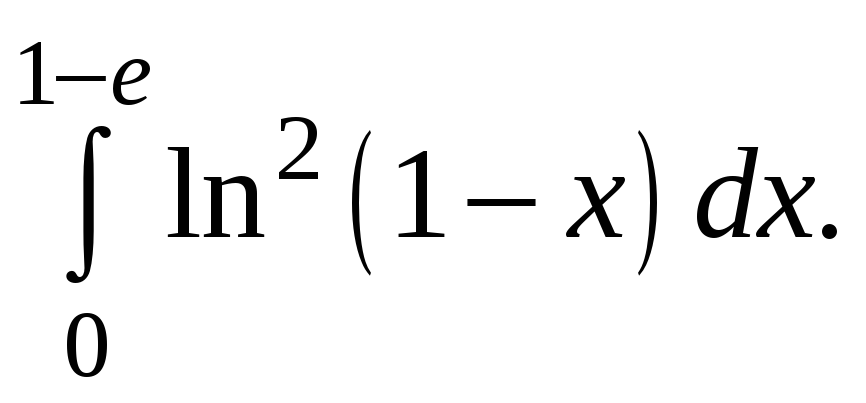Решение

Интегрируем по частям дважды:

4. Решить дифференциальное уравнение .

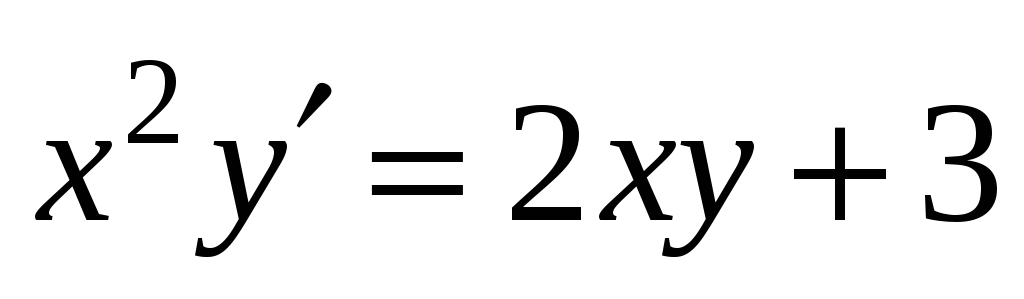Решение

Решаем это неоднородное уравнение первого порядка введением переменной у как произведения функций с последующей подстановкой непосредственно в уравнение:

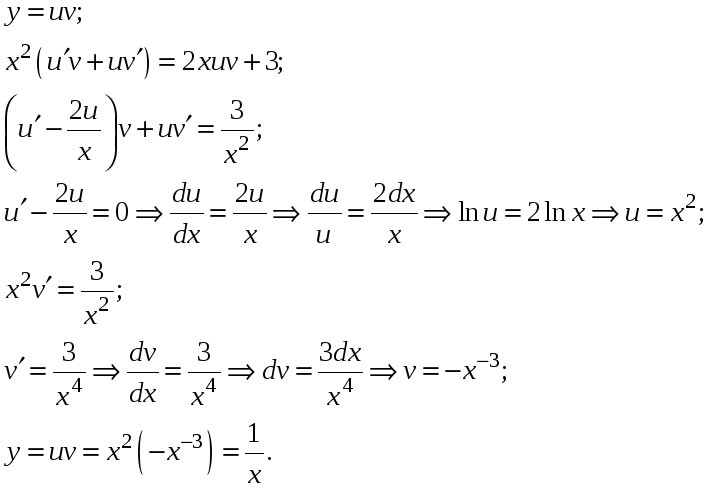
5. Вычислить площадь фигуры, ограниченной линиями:

(фигура расположена в верхней полуплоскости).

Решение

- данные линии (гипербола и две прямых и ) образуют две ограниченных области, одна из которых лежит в верхней полуплоскости.

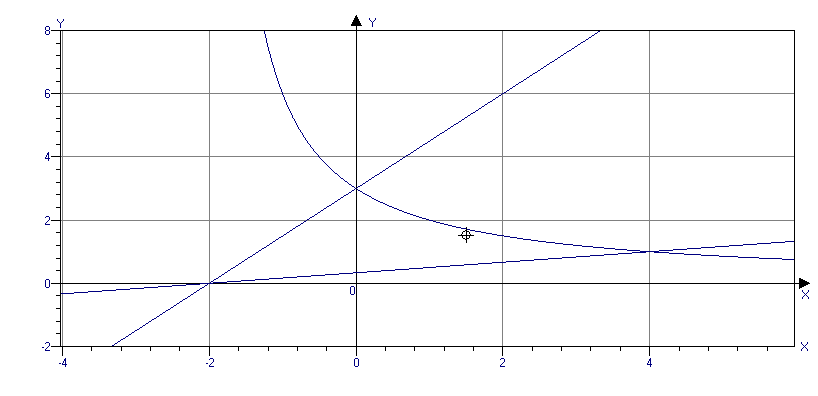
Точками, образующими искомую являются А(-2;0), В(0;3) и С(4;1). Площадь полученной сложной фигуры АВС, можно представить как сумму площадей элементарных фигур: прямоугольного треугольника АВ0 и криволинейной трапеции 0ВСС₁ минус площадь прямоугольного треугольника АСС₁. Площади всех трёх элементарных фигур можно найти с помощью интегрального исчисления:

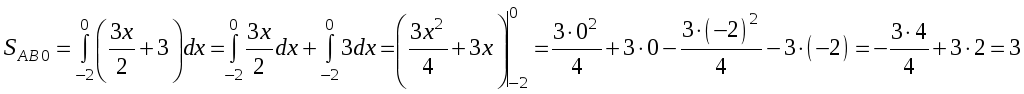кв. ед.

кв. ед.

кв. ед.

Окончательно кв. ед.

Можно было площади прямоугольных треугольников вычислить и без применения интегрального исчисления по формулам, известным из геометрии:

кв. ед. и

6. Экспериментальные данные о значениях переменных х и у приведены в таблице:

	0	1	2	4	5
	2,1	2,4	2,6	2,8	3,0

В результате их выравнивания получена функция . Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью (найти параметры ). Выяснить, какая из двух функций лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертёж.

Решение

Найдём параметры линейной регрессии из системы нормальных уравнений метода наименьших квадратов, для чего составим вспомогательную таблицу:

i	xi	yi	xi2	yi2	xi yi	увыравн			(yi -)2
1	0	2,1	0	4,41	0	2,0	0,0100	2,18	0,0064
2	1	2,4	1	5,76	2,4	2,26	0,0196	2,35	0,0025
3	2	2,6	4	6,76	5,2	2,44	0,0256	2,51	0,0081
4	4	2,8	16	7,84	11,2	2,71	0,0081	2,84	0,0016
5	5	3,0	25	9,0	15,0	2,82	0,0324	3,01	0,0001
	12	12,9	46	33,77	33,8	-	0,0957	-	0,0187

Параметры уравнения линейной регрессии:

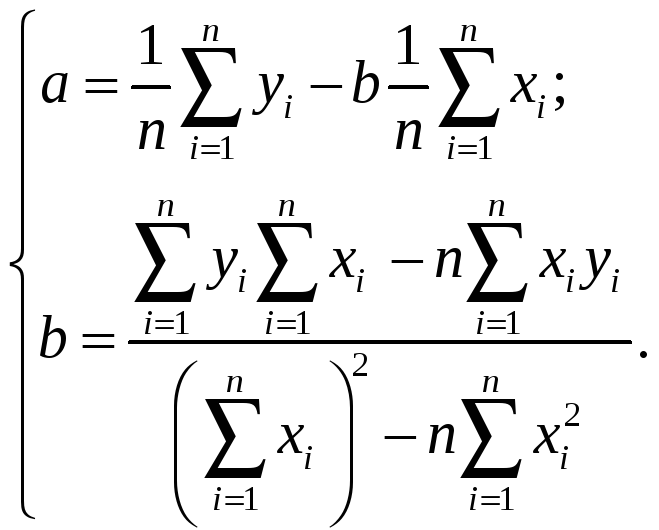
Откуда получаем:

Тогда

Следовательно, уравнением регрессии будет

После этого заполняем оставшиеся столбцы таблицы, вычисляя значения аппроксимирующих функций и суммы квадратов отклонений значений аппроксимирующих функций от эмпирических значений ряда. Сравнивая суммы квадратов отклонений, делаем вывод о том, что в смысле метода наименьших квадратов (сумма квадратов отклонений по ряду в целом) лучше выравнивает ряд линейная зависимость

7. Найти область сходимости степенного ряда .

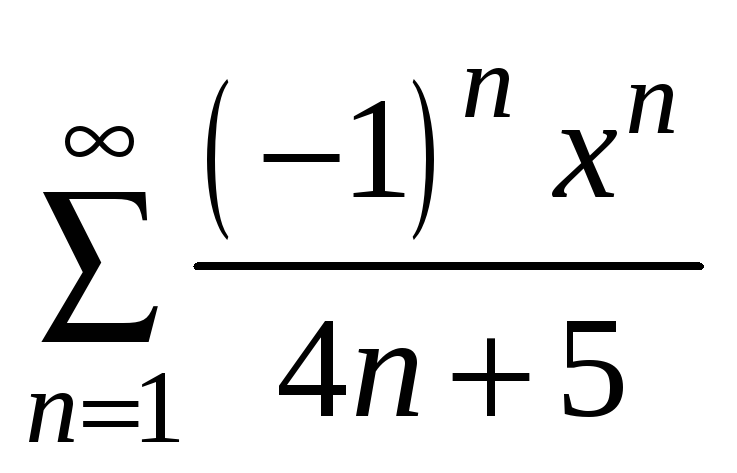Решение

Применив к ряду модулей признак Даламбера, получаем радиус сходимости:

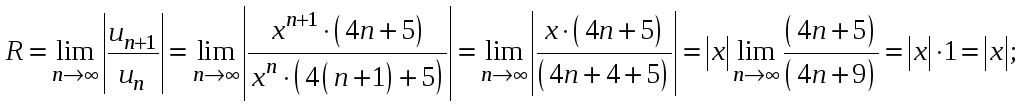
Следовательно,

Проверяем сходимость ряда на концах интервала сходимости:

При х=1 и при х=-1 получаем знакопеременные ряды, состоящие из элементов ряда эквивалентного гармоническому, следовательно (по признаку Лейбница) эти ряды сходятся условно (не абсолютно).

Таким образом, область сходимости