Калинин / Приборостроителям / Математика 1 (2)

Вариант №7

1. Найти пределы:

а) ; б)

2. Найти производные:

а) ; б)

3. Найти полный дифференциал функции двух переменных и все её производные второго порядка: .

4. Исследовать функцию двух переменных на экстремум:

.

5. Исследовать функцию и построить её график: .

6. Найти неопределённые интегралы и один результат проверить дифференцированием:

а) 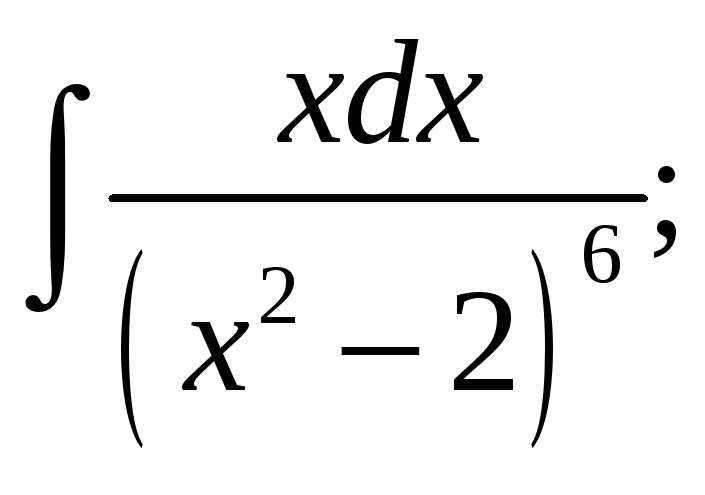б) .

7. Найти общее и частное решение дифференциального уравнения

8. Найти область сходимости степенного ряда:

а) ; б).

9. Разложить в ряд Маклорена следующие функции.

1. Найти пределы:

а) для раскрытия неопределённости использовали деление на старшую степень;

б) для раскрытия полученной неопределённости применим логарифмирование с последующим преобразованием

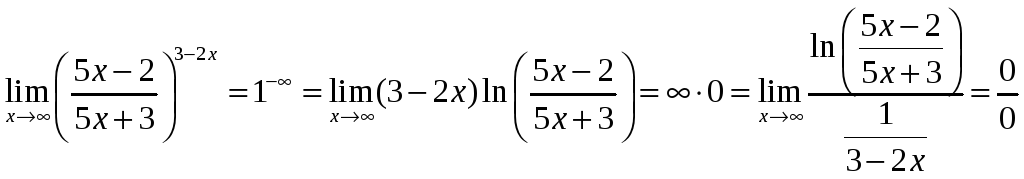
Для раскрытия данной неопределённости применяем правило Лопиталя-Бернулли. Дифференцируем по отдельности числитель и знаменатель, затем преобразуем.

Для раскрытия полученной неопределённости разделим числитель и знаменатель на старшую степень

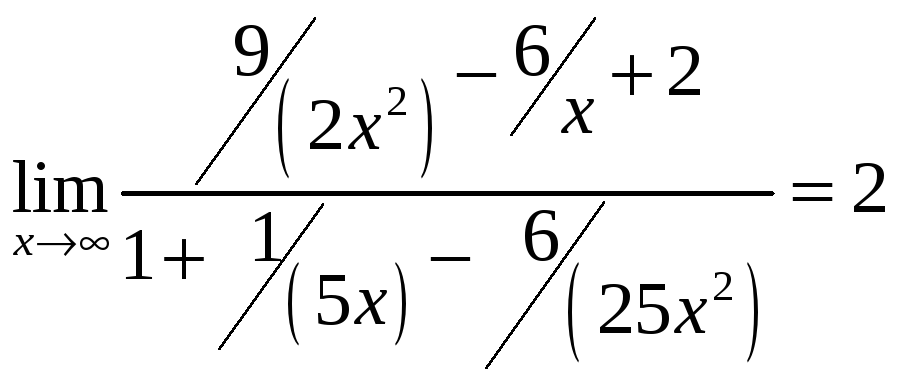
Таким образом, значение данного предела будет

2. Найти производные:

а) ; найдём, как производную сложной функции

б) , найдём, как производную неявной функции, через обратную производную, рассматривая неявную функцию как сложную

3. Найти полный дифференциал функции двух переменных и все её производные второго порядка: .

Дифференциал функции двух переменных

Вторые производные

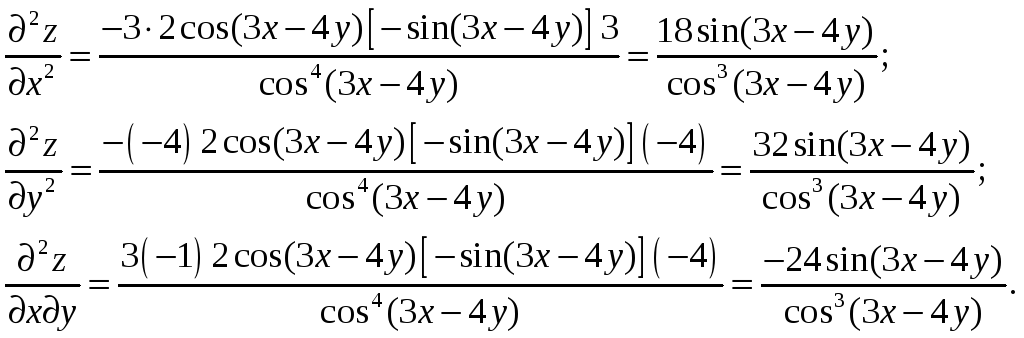
4. Исследовать функцию двух переменных на экстремум:

.

Для исследования функции двух переменных на экстремум найдём её первые производные:

Приравнивая первые производные нулю и решая совместно, определим особую точку функции:

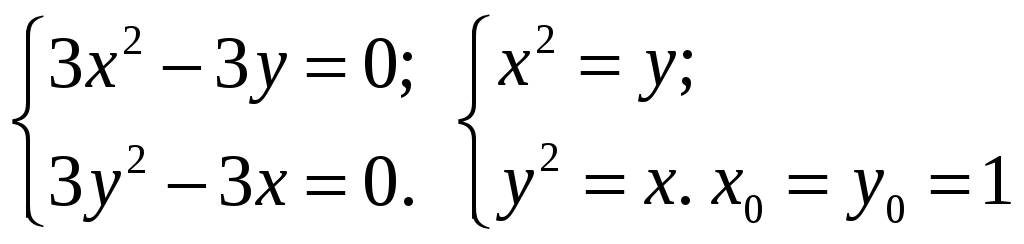
Для определения наличия и вида экстремума, найдём вторые производные функции и их значения в особой точке:

Составим определитель из полученных значений:

5. Исследовать функцию и построить её график: .

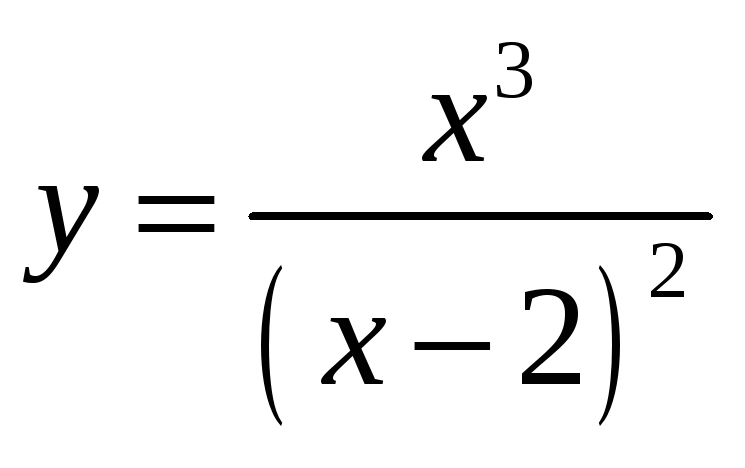Область определения функции: вся числовая ось за исключением точки х=2, через х=2 проходит вертикальная асимптота функции.

Областью значений функции является вся числовая ось.

График функции пересекает ось ОУ в точке х=0, ось ОХ также в точке х=0.

Функция имеет два интервала знакопостоянства: положительна при х>0 и отрицательна при х<0.

Для исследования интервалов монотонности функции найдём её первую производную:

Следовательно, у функции имеется одна особая точка х=6.

При х>6 функция возрастает, а при х<6 убывает, значит, точка х=6 точка максимума.

Для исследования интервалов выпуклости и вогнутости функции найдём её вторую производную:

Следовательно, точкой перегиба является точка х=0, при х>0 функция вогнута, при х<0 выпукла.

Функция имеет наклонные асимптоты, так как

Следовательно, уравнения правой и левой наклонных асимптот одинаковы у=х+2.

График функции строим по точкам:

х	0	1	3	-1	-2	-3
у	0	1	27	-0,111	-0,5	-1,08

6. Найти неопределённые интегралы и один результат проверить дифференцированием:

а) 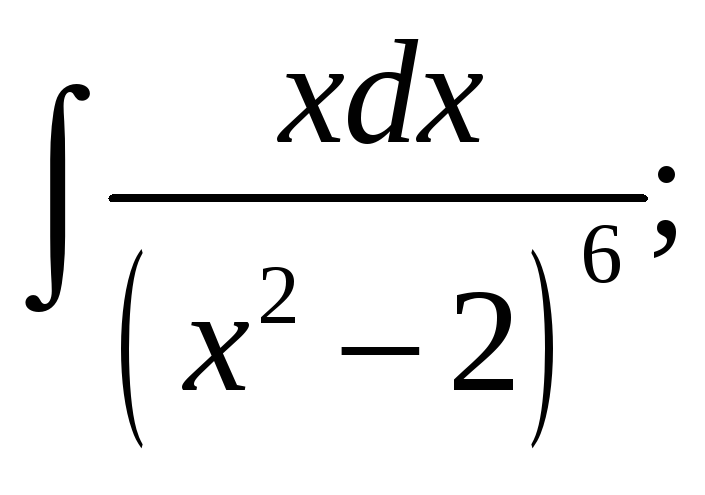применим метод замены переменных:

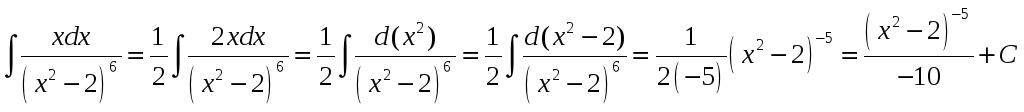
Проверка дифференцированием:

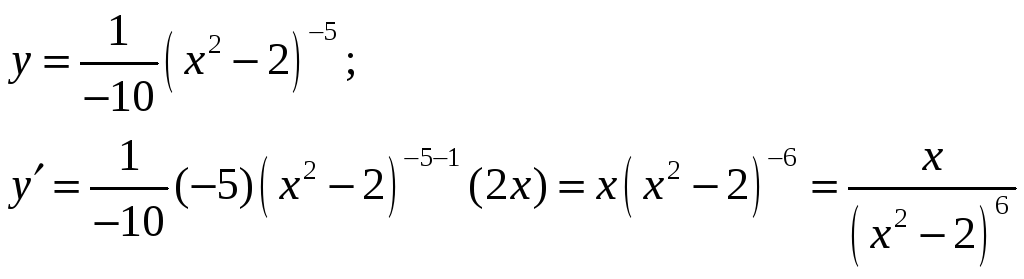
б) . Данный интеграл найдём интегрированием по частям:

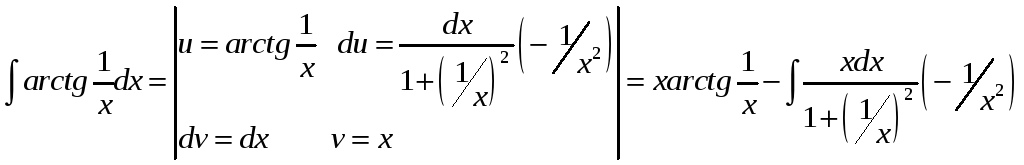
Возьмём второй интеграл отдельно, используя метод замены переменных:

И окончательно

.

7. Найти общее и частное решение дифференциального уравнения

Данное дифференциальное уравнение является неоднородным уравнением первого порядка.

Его решение распадается на решение однородного дифференциального уравнения с разделяющимися переменными и решение неоднородного уравнения. Таким образом решение данного уравнения будет состоять из общего решения однородного уравнения и частного решения неоднородного.

Частное решение будем искать методом вариации произвольной постоянной:

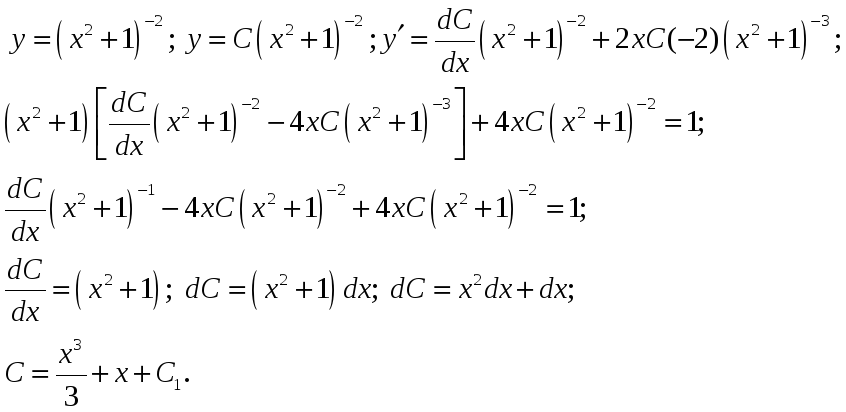
Тогда решение исходного неоднородного уравнения будет:

Окончательно, решением данного неоднородного уравнения первого порядка, удовлетворяющим начальным условиям будет:

.

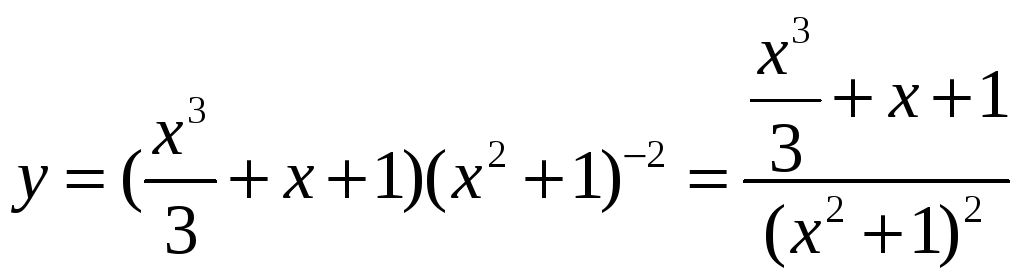8. Найти область сходимости степенного ряда:

а) ; на основании признака Даламбера

Область сходимости

Исследуем сходимость на границах интервала:

При х= получаем гармонический ряд , который расходится.

При х= получаем знакопеременный ряд , который на основании признака Лейбница сходится условно, так как соответствующий знакопостоянный ряд (гармонический ряд) расходится.

Следовательно, область сходимости:

б) на основании признака Даламбера

Область сходимости .

Исследуем сходимость на границах интервала:

При х= получаем гармонический ряд , который расходится.

При х= получаем знакопеременный ряд , который на основании признака Лейбница сходится условно, так как соответствующий знакопостоянный ряд (гармонический ряд) расходится.

Следовательно, область сходимости:

9. Разложить в ряд Маклорена следующие функции.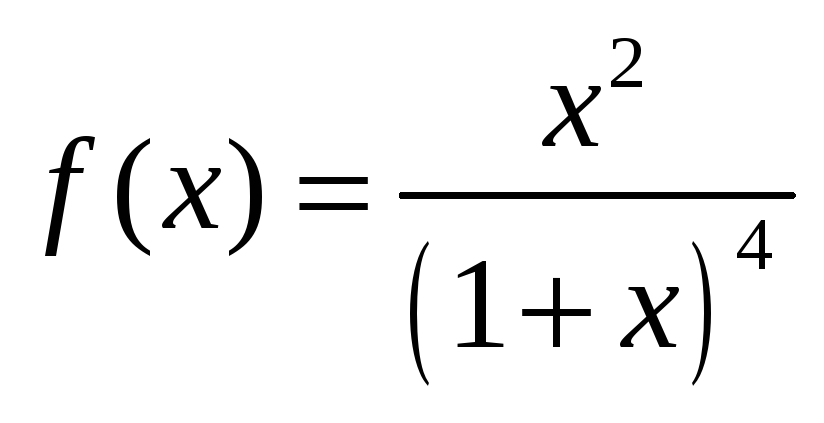

На самом деле

Найдём первые пять производных данной функции, и найдём значения функции и её производных в точке х=0:

Таким образом, разложение в ряд Маклорена для данной функции будет

,

Где – остаточный член

Окончательно получаем