Калинин / Приборостроителям / Математика 1 (17)

Задание для заочников групп КМЕН-091, 092

1 задание

1. Найти неопределенный интеграл (табл. 1).

а) ;

б) .

Решение

а) представляем интеграл как сумму интегралов, первый из которых интегрируется непосредственно ,а второй является табличным:

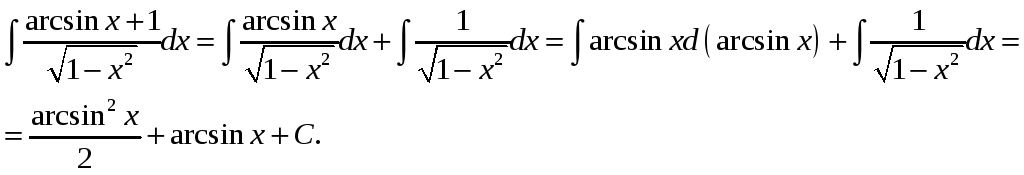
б) преобразуем подынтегральное выражение с использованием формул двойного угла и проинтегрируем непосредственно:

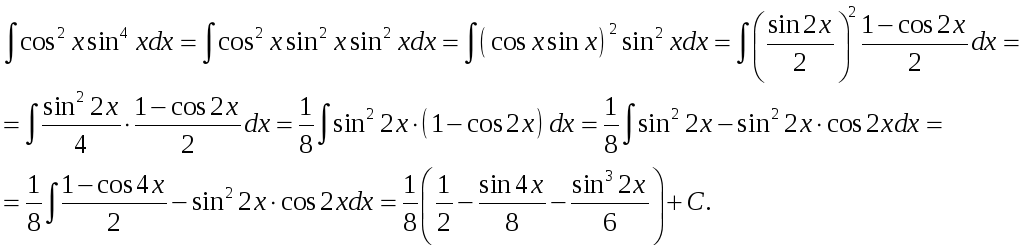
2. Вычислить определенный интеграл (табл. 2): .

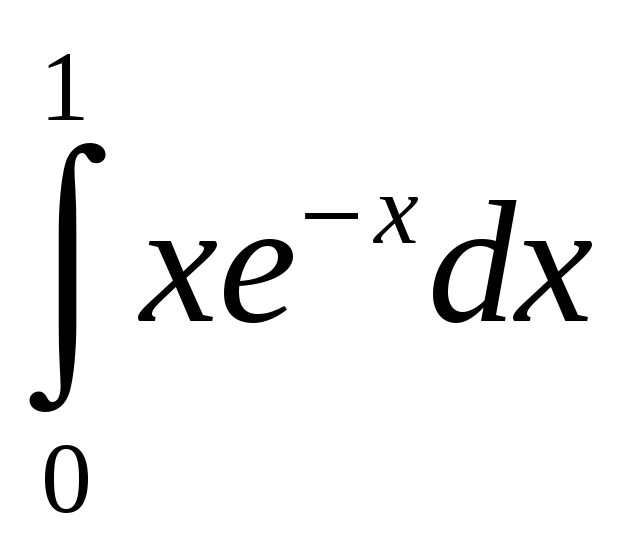Решение

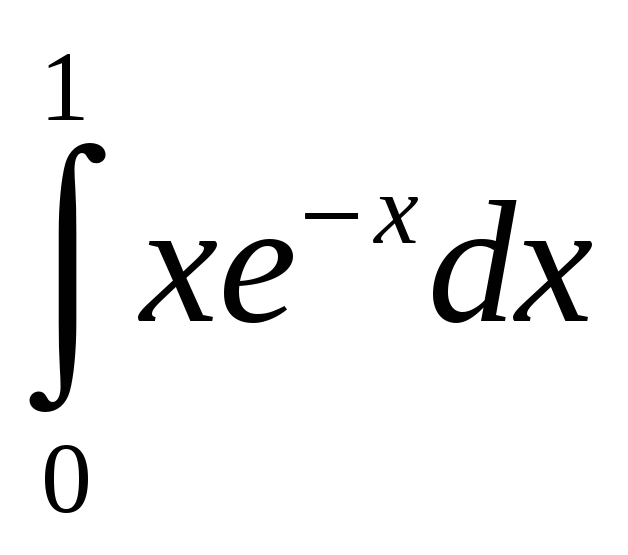- интегрируем по частям, а затем в результат вместо неопределённой константы интегрирования подставляем пределы интегрирования по формуле Ньютона-Лейбница:

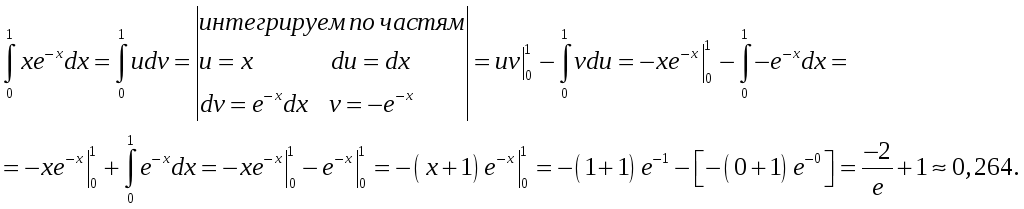
3. Вычислить площадь фигуры, ограниченной линиями (табл. 3).

.

Решение

Данные линии ограничивают криволинейный участок, площадь которого можно найти как разницу площадей под функцией и функцией .

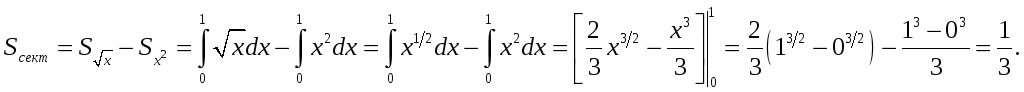
2 задание.

1. В партии из N изделий n изделий имеют скрытый дефект (табл.1). Какова вероятность того, что из взятых наугад m изделий k изделий являются дефектными?

N = 20; n = 5; m = 4; k = 2.

Решение

Вероятность скрытого дефекта в наугад взятой детали равна p = n/N = 5/20 = 0,25. Выбор любого числа изделий можно представить как бесповторную последовательную выборку, которая подчиняется тогда схеме испытаний Бернулли. Отсюда, вероятность вытянуть 2 дефектных изделий при выборе 4 изделий наугад из общей выборки равна:

2. В магазине выставлены для продажи n изделий, среди которых k изделий некачественные (табл.2.). Какова вероятность того, что взятые случайным образом m изделий будут некачественными?

k = 6; n = 16; m = 2.

Решение

Вероятность того, что взятое случайно изделие будет некачественным равна p = k/n = 6/16 = 3/8.

Каждое испытание (выборка изделия) независимо от остальных, поэтому вероятность взять случайно два подряд некачественных изделия равна произведению вероятностей: P(2) = 3/8∙3/8 = 9/64 = 0,140625.

3. На сборочное предприятие поступили однотипные комплектующие с трех заводов в количестве: n₁ с первого завода, n₂ со второго завода, n₃ c третьего (табл. 3). Вероятность качественного изготовления изделий на первом заводе p₁ на втором p₂, на третьем p₃. Какова вероятность того, что взятое случайным образом изделие будет качественным?

n₁ = 40; p₁ = 0,9; n₂ = 35; p₂ = 0,7; n₃ =25; p₃ = 0,9.

Решение

По формуле полной вероятности, вероятность события при требовании наступления до него предварительно другого события равна сумме произведений различных событий, приводящих к возможному наступлению, интересующего нас события, на вероятность наступления этого события если предворяющее событие уже произошло:

4. Дано распределение дискретной случайной величины Х (табл.4). Найти математическое ожидание и среднее квадратичное отклонение.

х	-6	-2	1	4
р	0,1	0,3	0,4	0,2

Решение

Математическое ожидание определяется как

Дисперсия при известном математическом ожидании определяется как

Среднее квадратическое отклонение есть корень квадратный из дисперсии:

5. В городе имеются N оптовых баз (табл. 5). Вероятность того, что требуемого сорта товар отсутствует на этих базах одинакова и равна p. Составить закон распределения числа баз, на которых искомый товар отсутствует в данный момент.

N = 3; p = 0,2.

Решение

Распределение числа баз, на которых искомый товар отсутствует в данный момент при равной вероятности отсутствия товара на каждой из баз подчиняется распределению вероятностей по схеме испытаний Бернулли:

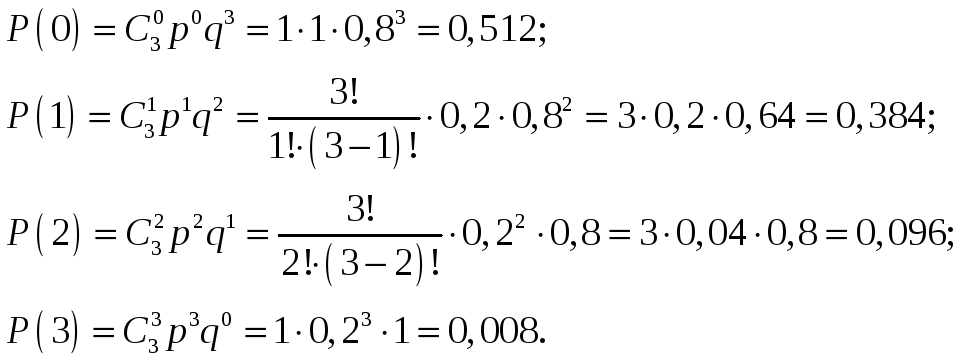
Таким образом, распределение числа баз, на которых искомый товар отсутствует в данный момент описывается следующей таблицей:

Число баз, на которых искомый товар отсутствует в данный момент	0	1	2	3
х	0,512	0,384	0,096	0,008

6. Непрерывная случайная величина имеет нормальное распределение. Её математическое ожидание равно М_х, среднее квадратичное отклонение (табл. 6.). Найти вероятность того, что в результате испытания случайная величина примет значение в интервале (a, b).

М_х = 14; = 3; a = 10; b = 15.

Решение

Вероятность попасть в какой-либо интервал для непрерывно распределённой величины равна:

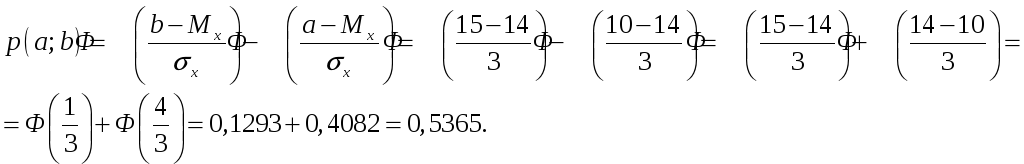
Воспользовались свойством нечётности функции Лапласа и стандартными таблицами значений функции Лапласа.

3 Задание

1. Рассчитать и построить гистограмму относительно частот по сгруппированным данным (табл. 1), где m_i – частота попадания вариант в промежуток (x_i; x_i+1).

i		mi
1	-6-2	2
2	-2-2	8
3	2-6	14
4	6-10	6
5	10-14	10

Решение

Расчёт гистограммы выполним в среде MS Office Excel, суммируя все частоты попадания и разделяя каждую частоту на всю сумму – для получения относительной частоты.

Гистограмма относительных частот строится по найденным значениям:

2. Найти несмещенную выборочную дисперсию на основании данного распределения выборки (табл.2).

распределение
xi	4	8	16	24
ni	31	14	28	27

Решение

Несмещённая выборочная дисперсия s(x) определяется на основании расчёта смещённой (эмпирической) дисперсии D(x). Для расчёта определим сначала полную сумму частот выборки: 31 + 14 + 28 + 27 = 100.

Математическое ожидание определяется как

Дисперсия при известном математическом ожидании определяется как

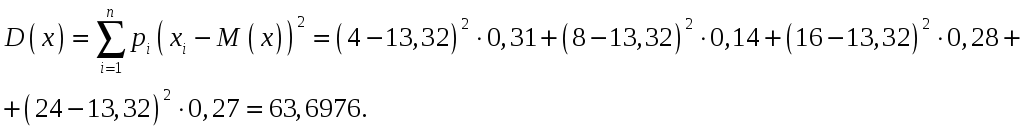
Тогда несмещённая дисперсия:

3. Проверить нулевую гипотезу о том, что заданное значение a₀ является математическим ожиданием нормально распределенной случайной величины при 5%-м уровне значимости для двусторонней критической области, если в результате обработки выборки объема n=10 получено выборочное среднее , а выборочное среднее квадратичное отклонение равно s₁ (табл.3).

a0		s1
20	18	2

Решение

Проверка нулевой гипотезы о том, что заданная величина является математическим ожиданием для нормально распределенной случайной величины заключается в вычислении величины

и последующем сравнении с квантилем нормального распределения, соответствующим заданному уровню значимости

Так как найденное значение U по модулю меньше, чем критическое значение, то нулевая гипотеза о том, что а₀ является математическим ожиданием не отвергается (принимается).

4. При уровне значимости проверить гипотезу о равенстве дисперсий двух нормально распределенных случайных величин X и Y на основе выборочных данных (табл. 4) при альтернативной гипотезе .

X		Y
xi	ni	yi	mi
39	4	75	4
43	2	80	2
45	3	84	3
47	4	91	4
51	2	94	2

Решение

Вычислим дисперсию по каждой выборке в отдельности, вычислив предварительно математическое ожидание, а затем сравним дисперсии, разделив большую из них на меньшую:

Математическое ожидание х определяется как

Дисперсия х при известном математическом ожидании определяется как

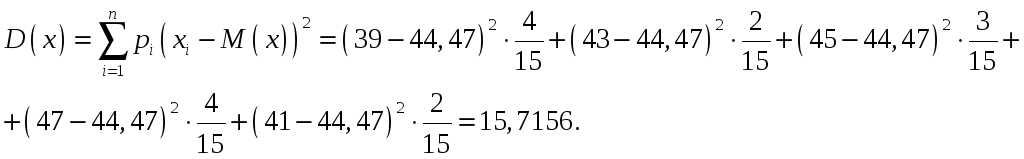
Математическое ожидание у определяется как

Дисперсия у при известном математическом ожидании определяется как

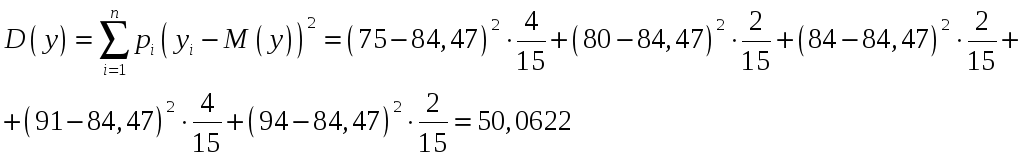
Разделим большую дисперсию на меньшую и получим F = 50,0622/15,7156 = 3,186 и сравним полученный результат с критерием Фишера при половинном уровне значимости и числе степеней свободы, уменьшенном на единицу – F_табл = 2,48 – по таблицам Фишера-Снедекора для уровня значимости 0,05 и 14 степенях свободы по каждой переменной. Таким образом, так как табличное значение критерия меньше расчётного, основная гипотеза о равенстве дисперсий отвергается (не принимается), а должна быть принята альтернативная гипотеза о неравенстве дисперсий двух данных выборок.

5. Найти выборочное уравнение линейной регрессии Y на X на основании корреляционной таблицы (табл.5).

Y\X	5	10	15	20	25	30	Частные суммы
14	4	6		8		4	22
24		8	10		6		24
34			32				32
44			4	12	6		22
Частные суммы	4	14	46	20	12	4

Решение

Вычисляем следующие суммы:

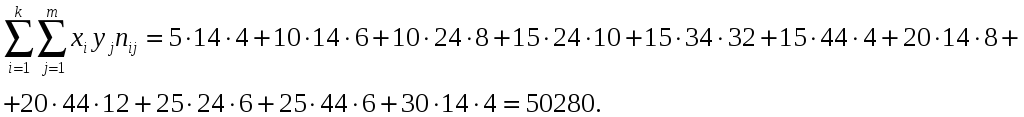
Вычисляем средние значения и дисперсии каждой величины:

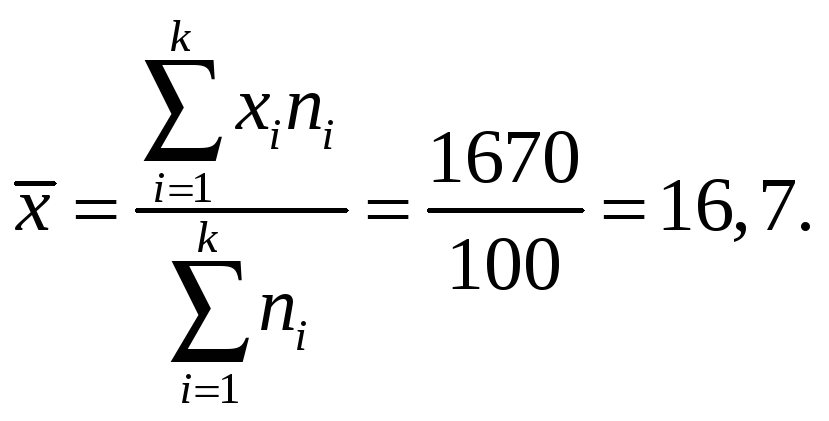
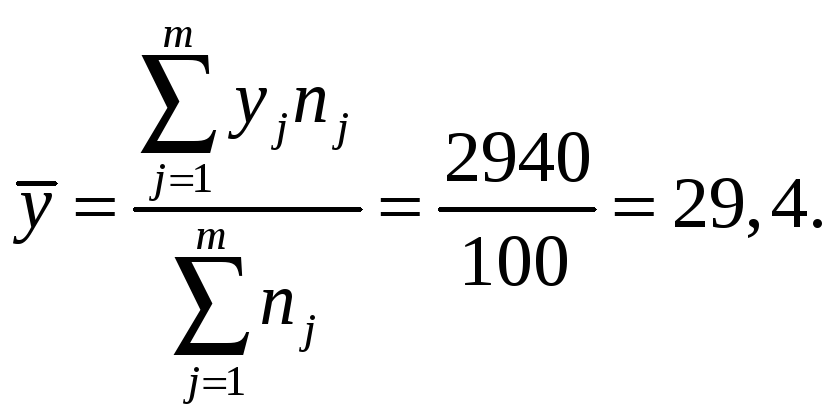
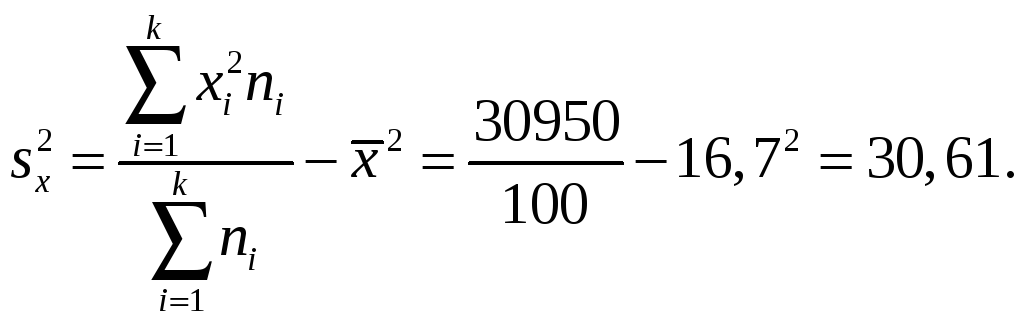
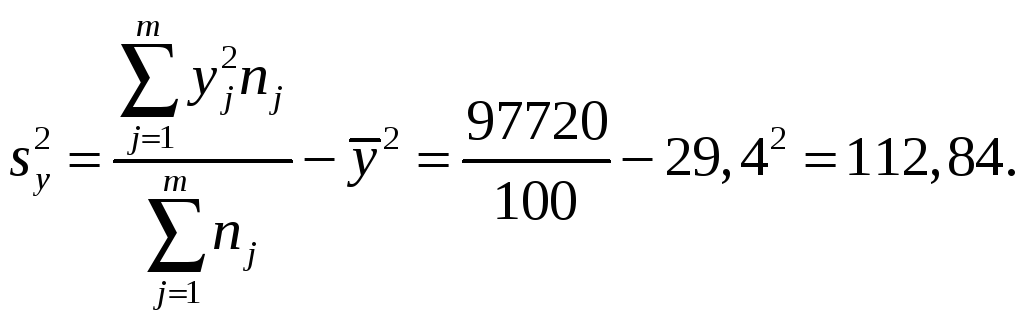
Вычисляем параметр μ:

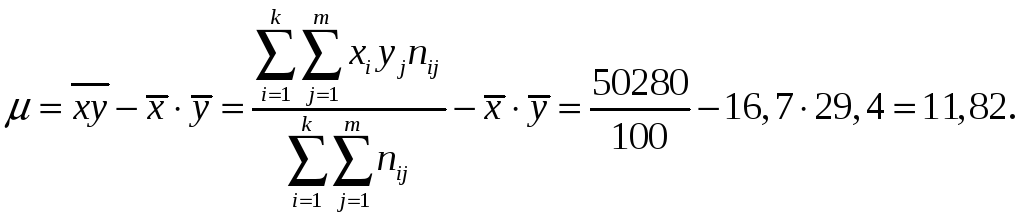
Теперь вычисляем коэффициенты b_xy и b_yx:

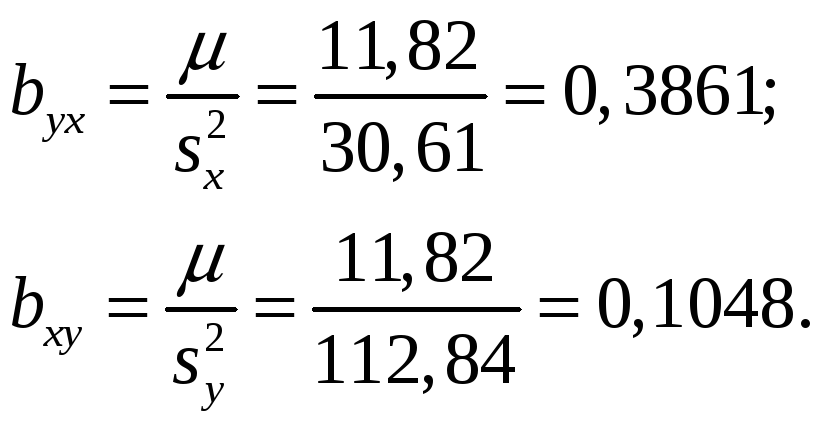
Теперь можно получить уравнения регрессии У на Х и Х на У в чистом виде:

Вычисляем коэффициенты искомого уравнения: