4.5.5. Система линейных однородных уравнений

Если свободные члены системы (2.1) все равны нулю, то получится однородная система уравнений:

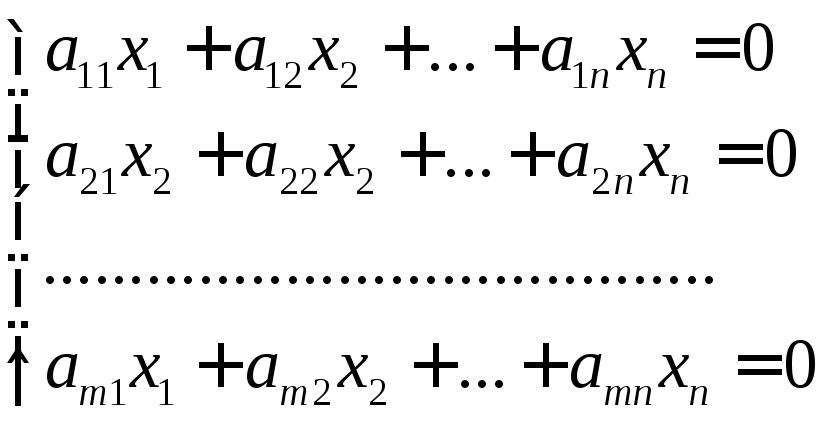(2.3)

Ранг основной матрицы системы (2.3) и ранг ее расширенной матрицывсегда равны, следовательно, однородная система всегда совместна. Нулевоерешение называемое тривиальным, является единственным, если В случае, когдасистема (2.3) имеет бесчисленное множество решений.

Пример 1. Решить систему уравнений

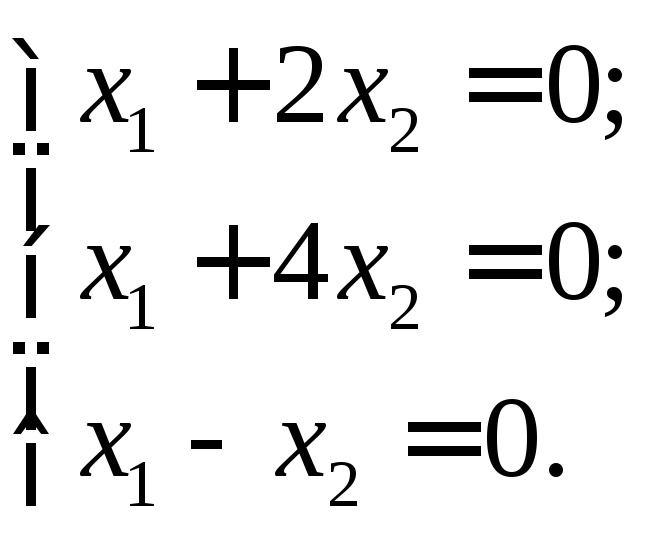
Решение. Преобразуем матрицу системы:

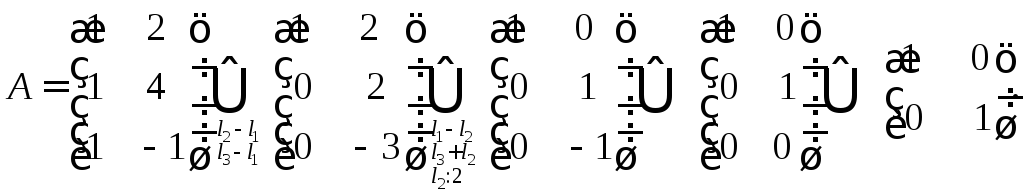
Полученная матрица, равносильная матрице данной системы, такова, что ее ранг равен двум и число неизвестных n = 2 , значит система имеет единственное решение

Пример 1. Решить систему уравнений

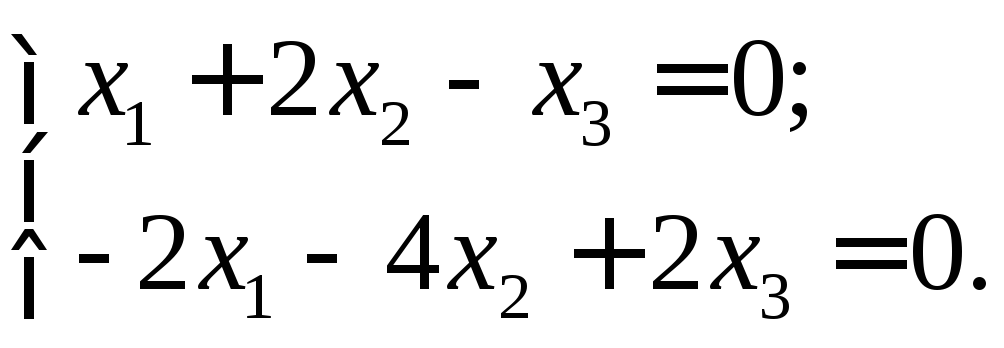
Решение. Составим матрицу 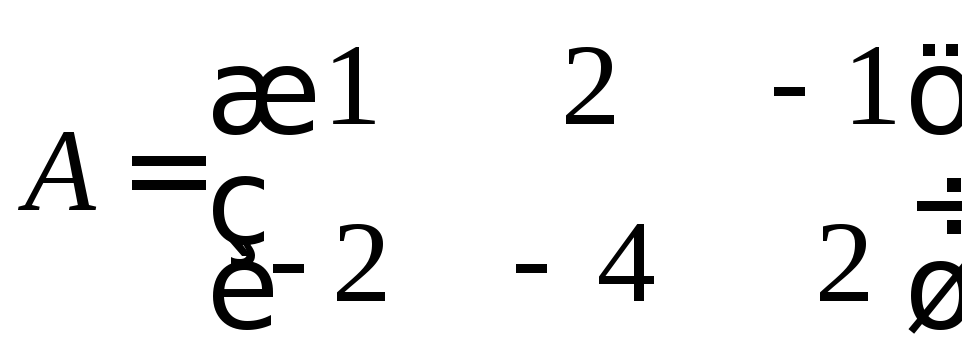системы и найдем ее ранг:

и .

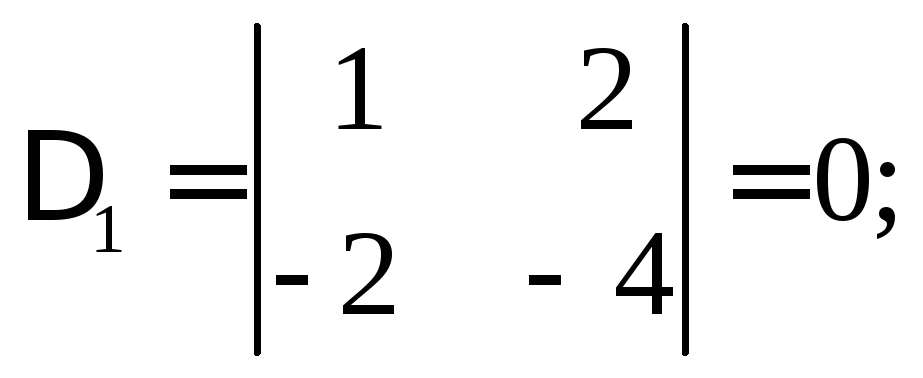
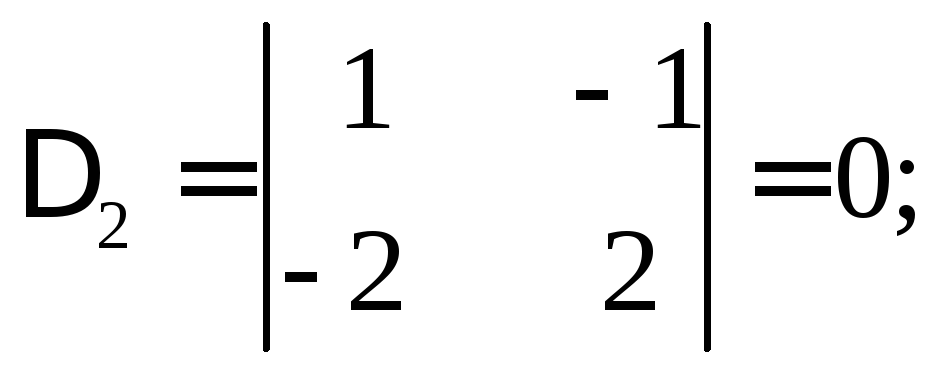
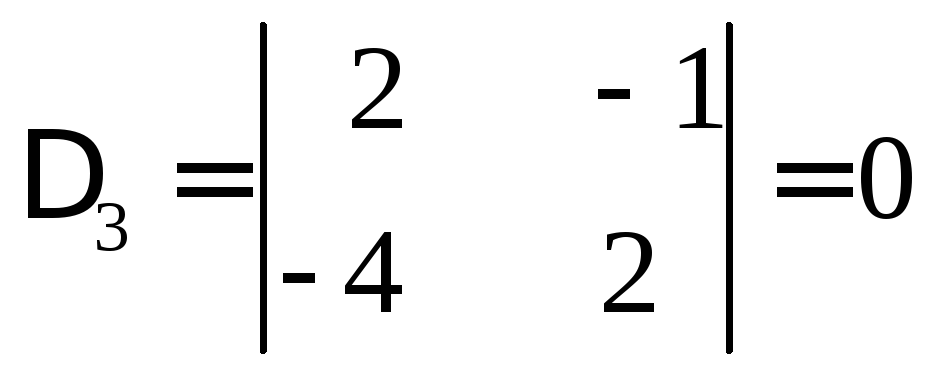Значит, т. к., например,

Итак, базисный минор тогда базисная переменнаяаи– свободные. Следовательно, решение системыгде– произвольные числа.

Если задать свободным переменным произвольные значения: гдеито бесчисленное множество решений системы примет вид: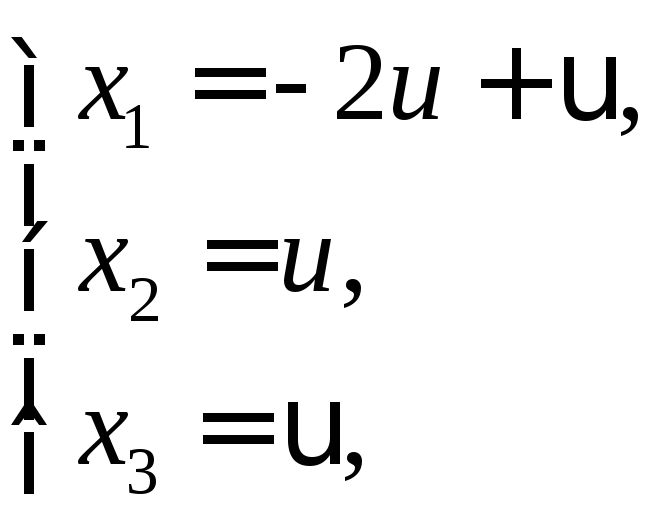гдеи

4.6. Собственные числа и собственные векторы матрицы

1. Всякий ненулевой вектор х называется собственным вектором матрицы А, если Ах = х, где  – некоторое число, называемое собственным значением (числом) матрицы

2. Если в некотором базисе вектор х и матрица А заданы:

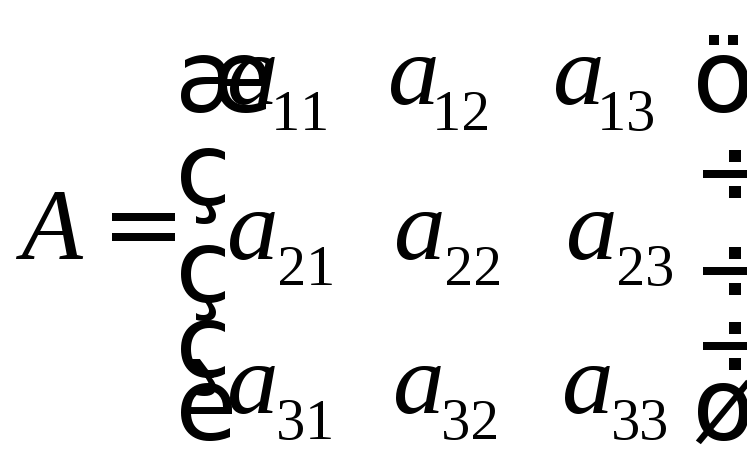и 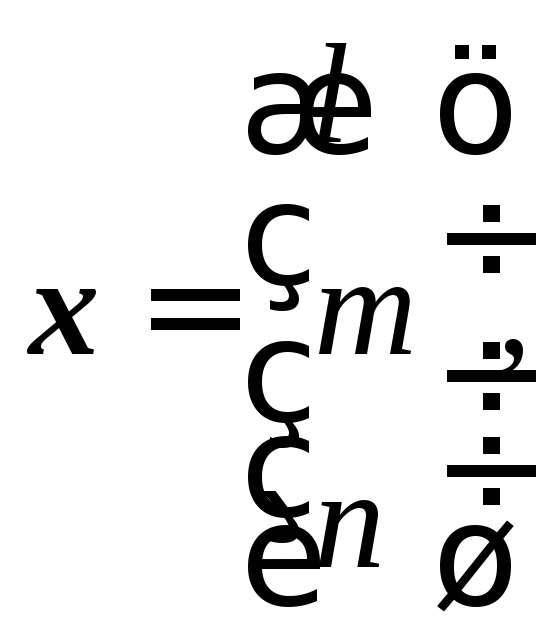то равенствуАх = х будет эквивалентна следующая система:

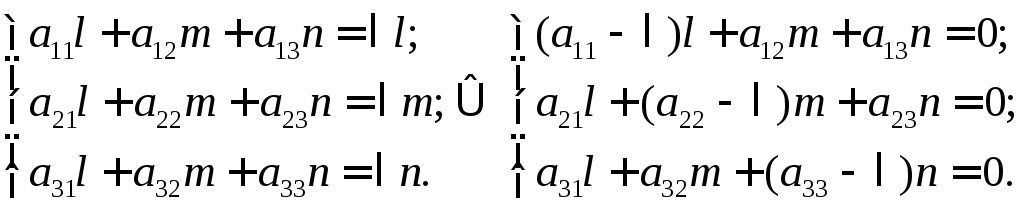(3.1)

Последняя однородная система относительно неизвестных l, m, n имеет всегда нулевое решение l = 0, m = 0, n = 0, т. е. х = 0, что нас не интересует. Ненулевое решение возможно тогда и только тогда, когда определитель этой системы равен нулю, т. е.

(*)

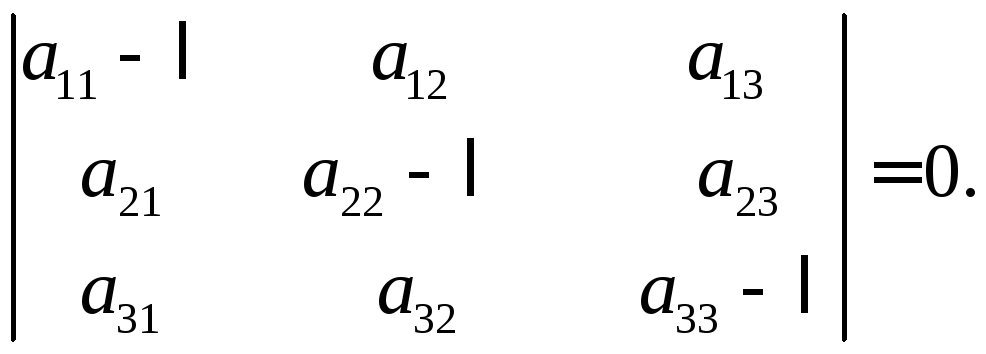Последнее равенство называется характеристическим уравнением.

Каждый действительный корень  этого уравнения является собственным числом матрицы А. Координаты собственного вектора, соответ-ствующего каждому собственному числу, находят из системы уравне- ний (3.1).

Замечание. Если х – собственный вектор матрицы А, то всякий, не равный нулю, коллинеарный ему вектор будет также собственным вектором матрицы А с тем же собственным числом.

Пример. Найти собственные значения и собственные векторы матрицы

Решение. Составим характеристическое уравнение (*):

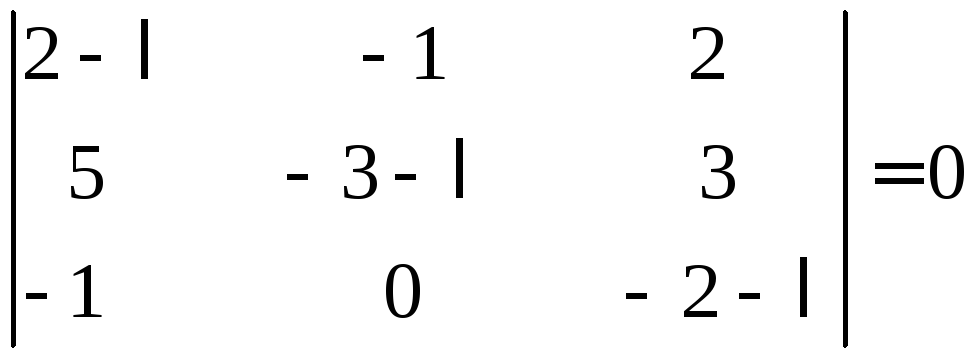и вычислим его корни:

Найденное собственное число  = –1 подставим в систему уравнений (3.1) и получим:

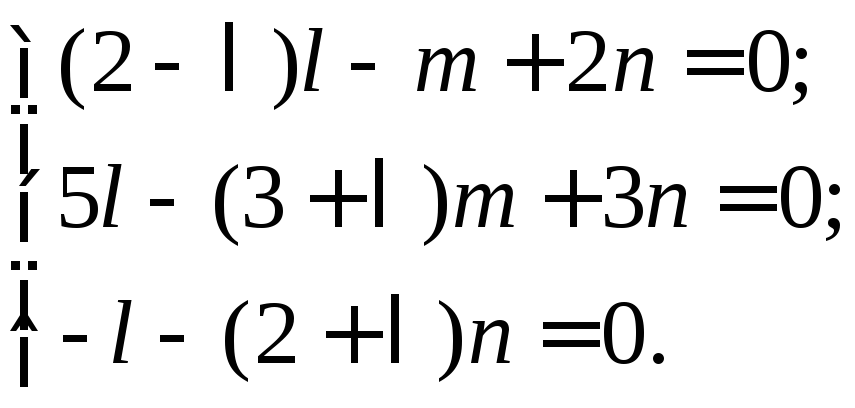
Решением последней системы являются числа:

где – собственный вектор данной матрицы.

5. Начала математического анализа

5.1. Понятие функции

Если каждому элементу х из множества D по некоторому правилу (закону) ставится в соответствие элемент у другого множества Е, то говорят, что между элементами (переменными) х и у существует функциональная зависимость; при этом переменную величину х называют независимой переменной, или аргументом, а переменную величину у – зависимой переменной, или функцией.

Функциональную зависимость между независимой переменной х и зависимой у записывают так:

или более подробно .

При этом множество D называется областью определения (или областью существования) функции, а множество Е – областью значения функции. Если функция f может быть задана на множестве N натуральных чисел:

, то такая функция называется функцией натурального аргумента, или числовой последовательностью с общим членом.

Если функция зависит от двух, трех и более аргументов, то она записывается следующим образом: или

Буква f является символом правила, по которому значениям аргумента ставятся в соответствие значения функции. Если при каком-либо исследовании рассматриваются различные функции, то при их символической записи могут использоваться различные буквы:

Функция считается заданной, если указано правило для определения значения функции, соответствующего данному значению аргумента. Такое правило может быть представлено различными способами. Наиболее часто встречающимися из них являются: аналитический, графический и таб-личный.