4.3. Действия над матрицами

4.3.1. Линейные действия над матрицами. Их свойства

● Пусть где

Если С = А + В, то Следовательно,чтобы сложить матрицы одного размера n  m, нужно сложить их соответствующие элементы.

● Произведением матрицы на число  0 называется матрица С = А, элементы которой есть элементы матрицы А, умноженные на , т. е.

Свойства линейных операций над матрицами

1. А + В = В + А; 2. А + (В + С) = (А + В) + С;

3. А + 0 = А (0 – нулевая матрица); 4. А – В = А + (– 1) ∙ В;

5. А + (– А) = 0; 6. 1 ∙ А = А;

7. (α + β) А = αА + βВ; 8. α(А + В) = αА + αВ;

9. α(βА) = (αβ)А, где А, В, С – матрицы, α и β – скаляры (любые действительные числа)

● Под элементарными преобразованиями матриц понимают следующие действия:

1) умножение всех элементов какой-либо строки (или столбца) на действительное число λ  0;

2) прибавление к элементам какой-либо строки (или столбца) величин, пропорциональных элементам другой строки (или столбца) (замена элементов строки (столбца) линейными комбинациями соответствующих элементов других строк (столбцов);

3) перестановку местами двух строк (или столбцов).

Матрицы называются эквивалентными, если одна может быть получена из другой с помощью элементарных преобразований.

● Если в прямоугольной матрице , размераn  m выделим k столбцов и k строк, причем k не больше наименьшего из чисел m и n и составим определитель из элементов, стоящих на пересечении выбранных строк и столбцов, то полученные указанным способом определители называются минорами матрицы А. Наивысший возможный порядок минора прямоугольной матрицы размера n  m равен наименьшему из чисел m и n. Для квадратной матрицы размера n наибольший возможный порядок минора равен n.

● Определение. Матрица имеет ранг r, если среди ее миноров существует хотя бы один, отличный от нуля, минор порядка r, а все миноры порядка r + 1 и выше равны нулю или не существуют.

Ранг нулевой матрицы считается равным нулю.

Пример. Для квадратной матрицы 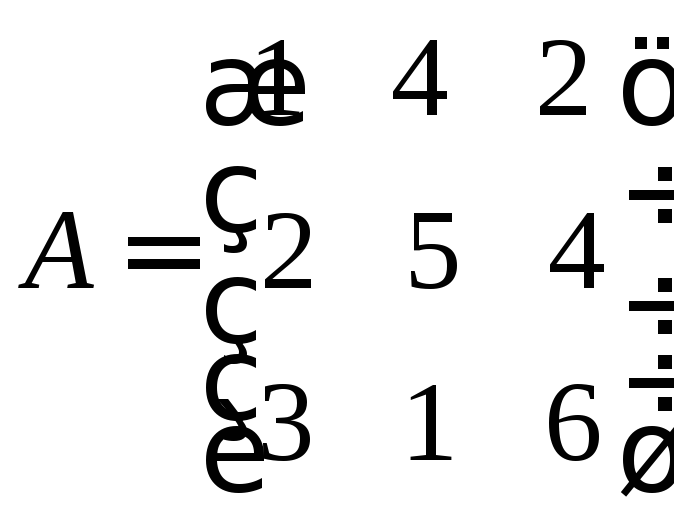порядкаn = 3 ее ранг r  3. Поскольку 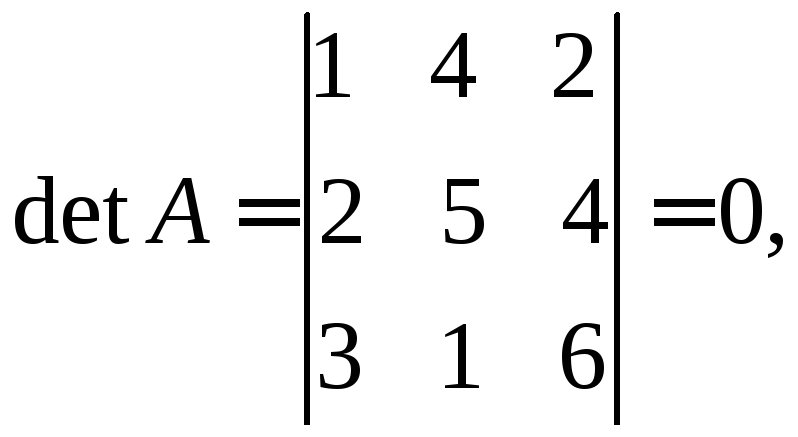но, например, составленный из элементов этой матрицы минор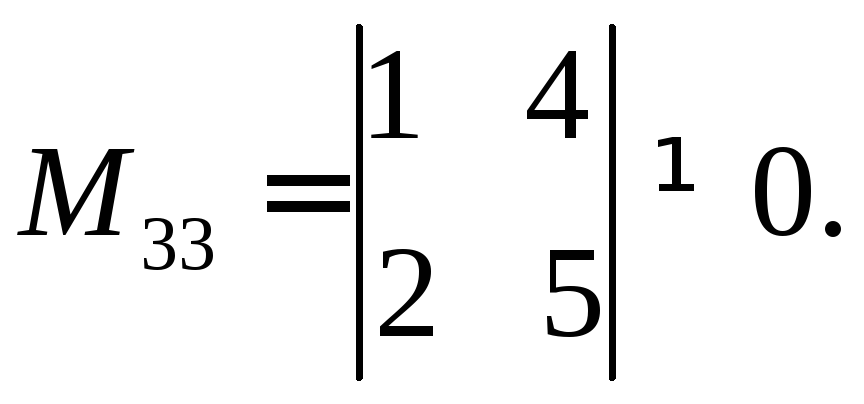Размерность этого минора равна 2, следовательно, ранг данной матрицыr = 2. Однако этот способ определения ранга матрицы не всегда прост. Удобнее привести данную матрицу А к так называемой ступенчатой форме, что возможно с помощью элементарных преобразований. Матрица ступенчатой формы такова, что все «диагональные» элементы, гдеотличны от нуля, а все элементы, расположенные под этой диагональю, равны нулю:

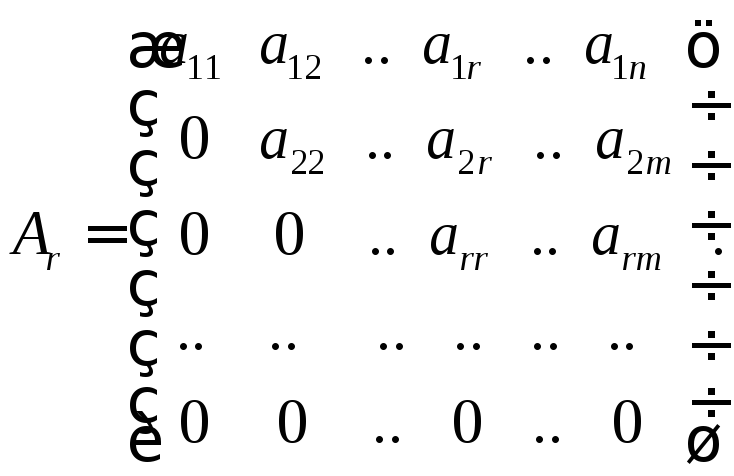
Число r элементов стоящих на главной диагонали, не зависит от способа приведения прямоугольной матрицыА к виду ступенчатой матрицы А_r и называется рангом матрицы А.

Следствие. Ранги двух эквивалентных матриц равны.

● Операция над матрицей при которой ее строки становятся столбцами с теми же номерами, а столбцы – строками, называетсятранспонированием. Обозначается транспонированная матрица

Операция транспонирования обладает следующими свойствами:

1. 2.

3. 4.

● Произведение матрицы А на матрицу В определяется только в случае, если число столбцов матрицы А равно числу строк матрицы В. В этом случае матрицы А и В называются согласованными.

Замечание. Из того что матрица А согласована с В, а значит существует матрица АВ, не следует что матрицу В можно умножить на А, т. к. из согласованности А с В не следует согласованность В с А. Следовательно, в общем случае АВ  ВА. Однако АЕ = ЕА.

Действие умножения матриц выполняется по принципу «строка на столбец», что схематично представлено на рис. 24.

П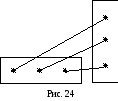роизведением матрицына матрицуназывается такая матрицаэлементы которойравны сумме произведений элементовi-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В:

Примеры. Найти АВ и ВА, если:

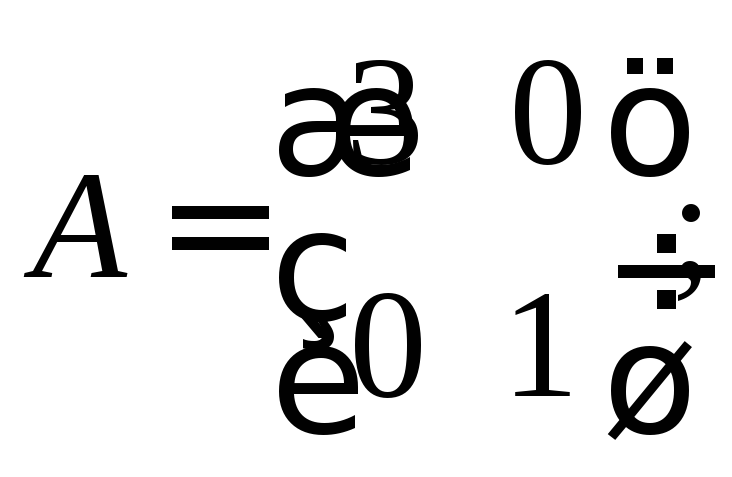
1) 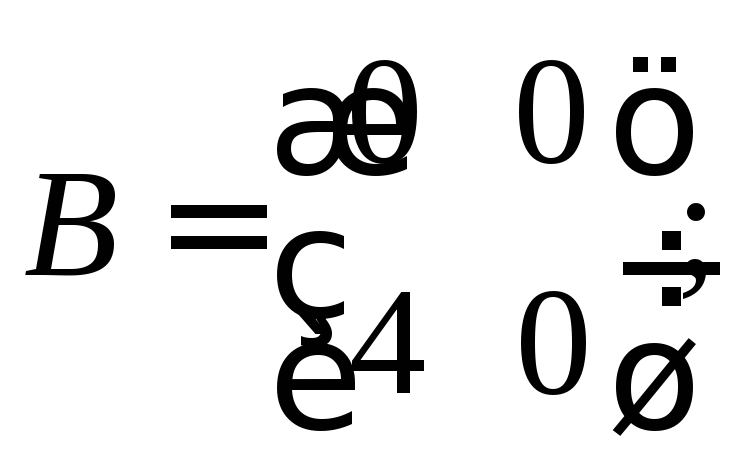2)

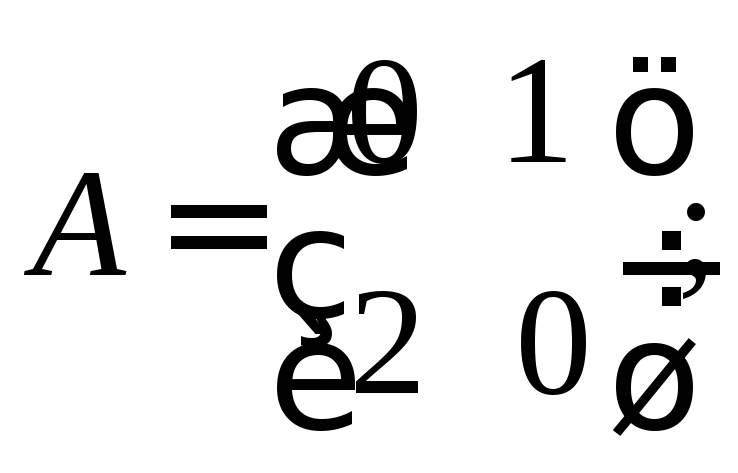
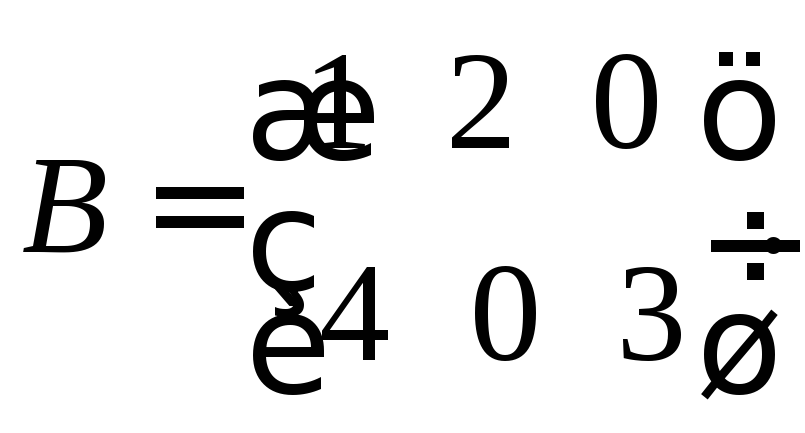
Решение. 1) А согласована с В и В согласована с А, значит, существуют матрицы АВ и ВА:

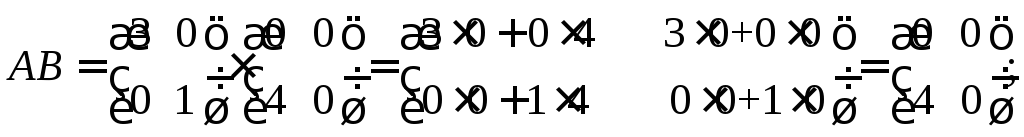
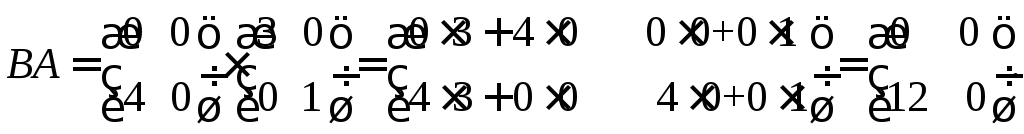
Итак, существуют матрицы АВ и ВА, однако АВ  ВА.

2) Матрица А с В согласована, значит существует АВ:

Но матрица В не согласована с А, следовательно, произведение матриц ВА не существует.